如何理解“求捆瓶子中繩長”問題中的圓弧拼合部分

顏麗霞

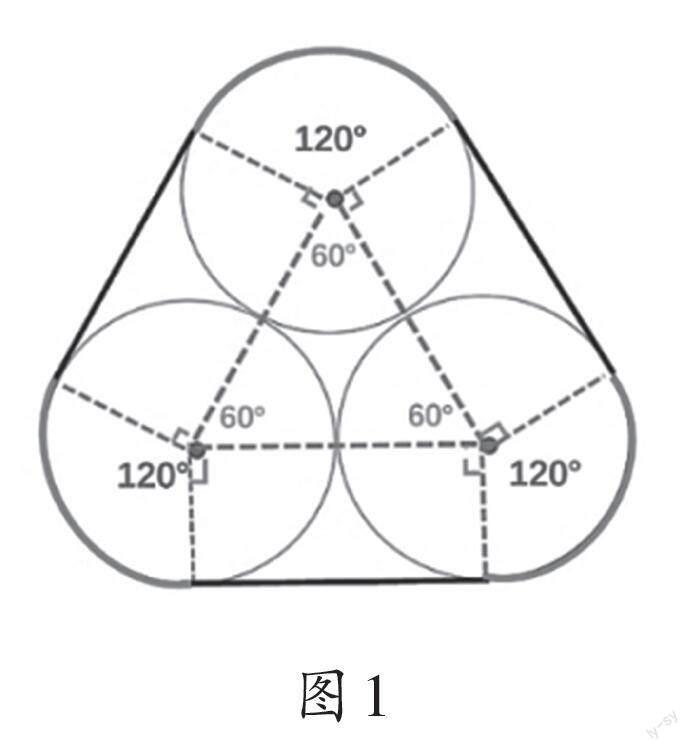
《教學月刊·小學版》（數學）2023年第10期刊登了《如何更好地解決“求捆瓶子中繩長”問題》一文，該文有許多可圈可點之處。然而，文章在求捆三個圓柱形瓶子的繩長（如圖1）時，選擇直接告訴學生三角形的每個內角為60°，三角圓弧所對應的圓心角為120°，這一做法存在一定的問題。經筆者研究發現，許多學生在理解如何確定三角形每個內角為60°以及每條圓弧所對應的圓心角為120°等方面存在困難。此外，理解“三條圓弧的長度之和等于一個圓的周長”這一規律，對學生來說也有較大難度。為幫助學生解決這些難點問題，可以采用以下教學過程。

一、動態感知，想象移拼

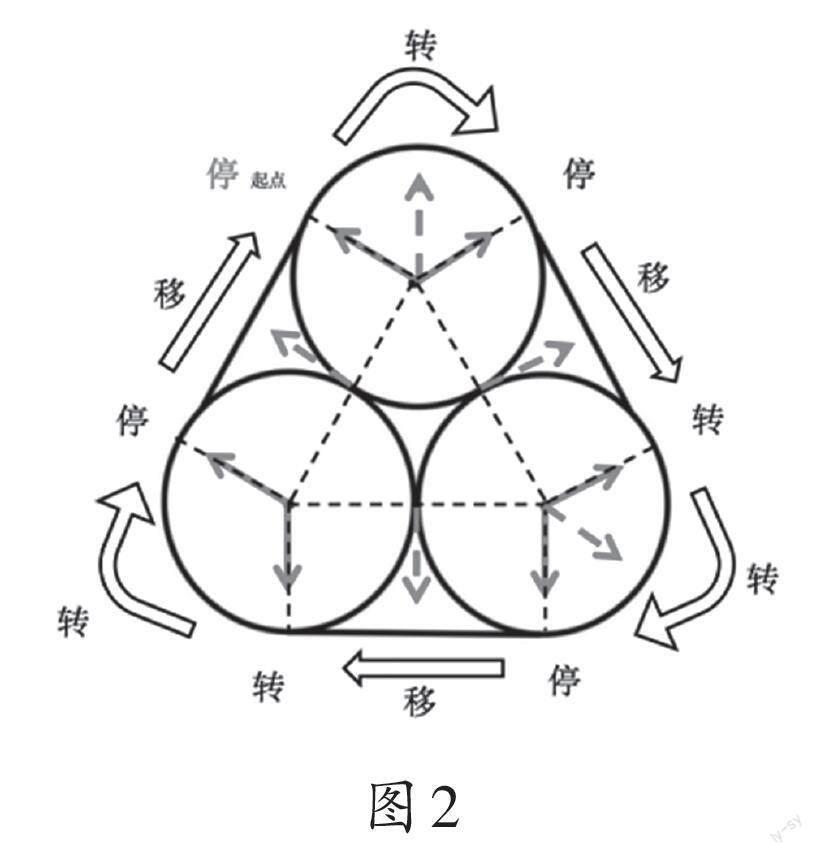
教師呈現示意圖（如圖2），要求學生自主操作，用筆尖代替圖中的箭頭，從起點開始轉一周，描出捆三個圓柱形瓶子的繩長，邊描邊思考，圓弧部分拼成了什么圖形？

學生獨立完成操作后反饋：筆尖從起點出發，沿著箭頭轉一周，發現筆尖所經過圓弧部分的路徑恰好為一個圓形。因此，圓弧部分拼起來的長度正好為圓的周長。

二、畫圖表征，推理說明

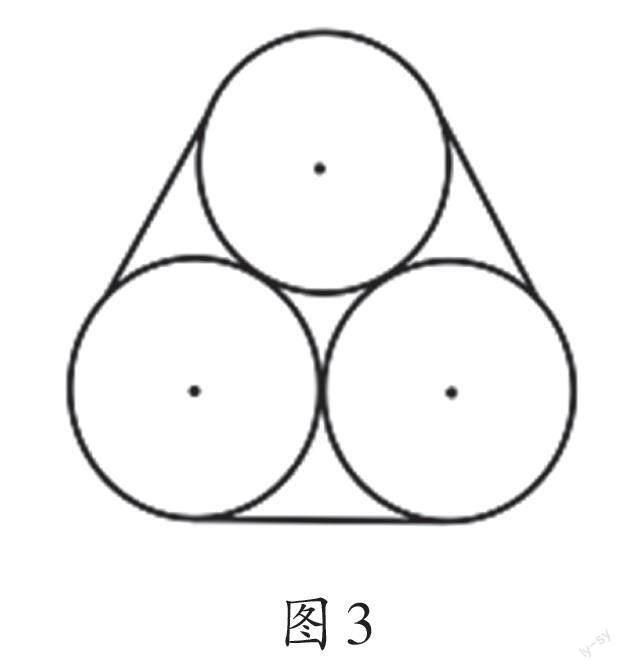
教師出示圖3，讓學生獨立嘗試畫分割線。

學生獨立嘗試后，教師直觀演示畫圖方法：將相鄰兩個圓的圓心連接，得到一條線段。分別通過這兩個圓心作這條已知線段的垂線（即圓的半徑），并連接半徑與圓相交的兩點，從而得到繩子的線段部分，從而將繩子分為圓弧和直線兩部分（如圖1）。

接著引導學生思考：（1）連接相鄰兩個圓的圓心所形成的線段長度是多少？……