靜聽思維拔節的聲音

林迪　林志輝

［摘 要］借助“圖形運動（三）解決問題”練習課，利用拼七巧板的問題情境，以“如何運動計分最低”這個關鍵問題，引導學生描述每一塊板如何從起始位置運動到目標位置，驅動學生主動地進行觀察、操作、想象、推理等活動。在語言和操作表征的互通中，學生有效聯結圖形的運動知識。在既有意義又有意思的數學活動中，學生思維逐次拔節，發展了空間觀念和推理意識。

［關鍵詞］思維；空間觀念；推理意識

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2024）02-0072-03

“圖形運動（三）解決問題”練習課的教學要讓學生能在方格紙上描述簡單圖形的平移、旋轉、軸對稱變換的運動過程，在觀察、操作、想象、描述圖形運動過程中，進一步感悟平面圖形全等變換的特征，發展空間觀念和推理意識。以下是筆者的教學實錄。

一、輪廓劃分，思維初拔節

（一）關鍵板的推理

【教學片段1】

師：通過課前學習單（如圖1所示），大家嘗試了用七巧板拼搭小魚圖。在拼搭的過程中，你們先拼了幾號板？又是如何拼其他板的？

生1：我先確定①號板或②號板，因為它們的面積最大，最好確定。

生2：我先確定④號板，因為它的形狀特殊，它的4條邊相等，有4個直角。

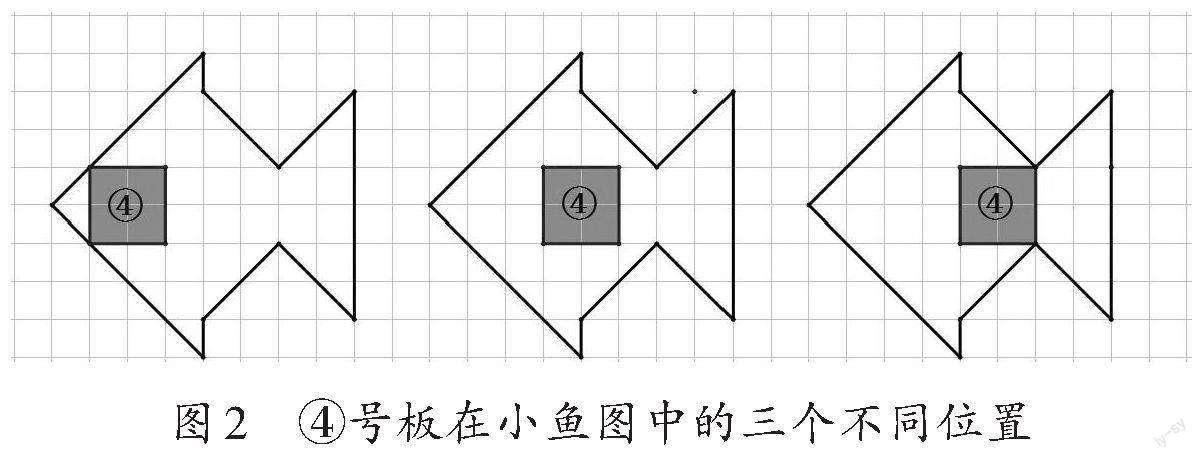
師：很多同學選擇了④號板，這里有三種④號板的擺放位置（如圖2），你同意哪一種？為什么？

生3：第三種。如果④號板的擺放位置是第一種或第二種，那七巧板中最大的①號板和②號板就擺不下了。

師：說一說按第三種擺放④號板后，其他板的位置。

生4：①號板和②號板在魚頭的位置，③號板和⑤號板分別在魚肚中間正方形的上下處，⑥號板和⑦號板在魚尾。

（教師讓生4操作幾何畫板。）

設計意圖：在前測中，有70%的學生需要借助實物劃分小魚圖輪廓。在本環節中，筆者首先讓學生自主選擇關鍵板，根據學生選擇最多的④號板開展教學，讓學生通過④號板的位置來推斷其他板的位置，從而感受到用推理和想象來解決問題。筆者利用幾何畫板的強大互動性，讓學生邊說明邊演示，直觀展示他們的想象和推理過程。這樣的設計旨在激發學生的思維，讓他們親身參與解決問題的過程，加深對數學知識的理解和記憶，并培養他們在數學學習中的興趣和積極性。

（二）任意板的推理

【教學片段2】

師：還可以先確定幾號板的位置，從而推理出其他板的位置？

生1：還可以先確定⑥號板和⑦號板的位置，因為小魚圖中⑥號板要和⑦號板放在一起，所以只能把它們放魚肚或魚尾，它們的位置確定了，①號板和②號板就只能放在魚頭，那其他板的位置也就確定了。

生2：還可以先確定③號板的位置，因為它只能放在魚身，或放在魚尾的最上方或最下方，它和⑤號板剛好是一上一下擺放，它的位置確定了，⑤號板的位置也就確定了。而③號板和⑤號板的中間只能擺④號板，再加上①號板和②號板在魚頭，其他板的位置也就確定了。

生3：我發現任意一塊板的位置確定了，就能根據板之間的形狀關系，確定其他板的位置。

設計意圖：利用“還可以先確定幾號板的位置”這樣的問題，能讓學生把根據④號板推理其他板的活動經驗遷移到任意板的推理過程中。從最初只有某一塊特定板是關鍵板，擴展為每一塊板都可能成為關鍵板，學生利用圖形幾何特征進行輪廓劃分，推理意識得到進一步發展。

二、運動描述，思維再拔節

（一）激活認知，喚醒經驗

【教學片段3】

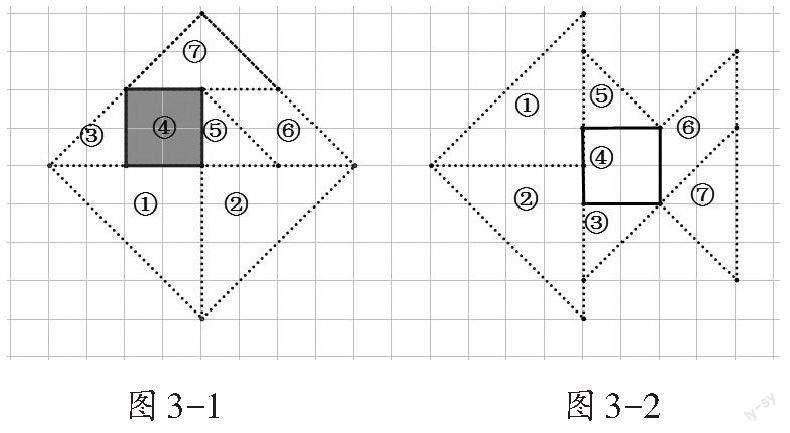
師：想一想，④號板是如何從圖3-1的位置運動到圖3-2的位置的？你能找出幾種不同的運動方法？如果運動1次記1分，哪種運動方法的分數最低？

生1：④號板先向下平移1格，再向右平移12格，運動了2次，記2分。

生2：④號板先向右平移12格，再向下平移1格，也是記2分。

（教師利用幾何畫板動態演示學生的方法。）

設計意圖：通過描述④號板的運動路徑，喚醒學生描述圖形運動的數學學習經驗。

（二）自主探究，表征互譯

【教學片段4】

師：請將⑦號板從圖4-1的位置運動到圖4-2中，并記分。

生1：⑦號板繞點C逆時針旋轉90°，向右平移12格，向下平移1格，記3分。

生2：⑦號板繞點A逆時針旋轉90°，向右平移12格，向下平移5格，記3分。

生3：⑦號板繞點B逆時針旋轉90°，向下平移5格，向右平移16格，記3分。

設計意圖：學生通過語言、操作積累組合運動的描述經驗，能夠更好地理解和運用圖形與幾何的概念和原理，同時提高表達能力和思維的靈活性，空間觀念也得到提升和發展。

（三）逐板分析，思維拔節

【教學片段5】

師：有哪些板的運動計分是2分？利用學習單想一想、寫一寫。

生1：①號板需要1次旋轉和1次平移，⑤號板需要平移兩次，因此都記2分。②號板需要1次平移和1次旋轉才能運動到目標位置，記2分。

生2：不對，②號板只要1次軸對稱運動就可以了（圖略），這樣只記1分。

生3：那其他板也可以用軸對稱的方法，這樣能夠減少運動的次數。

師：大家一起試試吧。

設計意圖：借助“哪些板的運動記分是2分”的問題，促使學生主動思考，并以②號板作為突破口，喚醒學生對軸對稱運動的學習經驗。

三、聯結融通，思維三拔節

（一）推理想象拼帆船

【教學片段6】

師：七巧板不僅可以拼成小魚圖，還可以拼成帆船。看帆船圖（圖略），你把幾號板當作關鍵板？

生1：①號板和②號板，因為它們的面積最大。

師（出示圖5-1、5-2、5-3）：有三位同學確定了①號板和②號板的位置，你贊成哪種想法？

生2：我贊成圖5-2的擺法。因為如果按圖5-1和圖5-3的擺法，④號板和⑥號板就不能同時擺進去，會有部分超出帆船的輪廓。

設計意圖：本環節利用將七巧板拼成帆船圖的問題情境，引導學生正向遷移通過想象推理劃分輪廓的數學活動經驗，展現嚴謹的推理思路。

（二）思考迭代算總分

【教學片段7】

師：想一想，在所有板的運動中，哪塊板的運動記分最低，是多少？

生1：④號板只需要1次平移就可以實現，記1分。

生2：我發現①～⑥號板都只需要1次軸對稱運動，都是記1分。

生3：我認為所有板的運動總分是6+3=9（分），因為①～⑥號板只需要1次軸對稱運動，共6分，⑦號板的運動記3分。

生4：我發現的方法總計分更低，因為①～⑥號板可以整體進行1次軸對稱，記1分，⑦號板的運動記3分，所以總計1+3=4（分）。

生5：我發現最低分是1+1=2（分），①～⑦號板整體進行1次軸對稱，共1分，⑦號板旋轉1次記1分。

（教師給予每個學生充分的時間進行空間想象，然后利用幾何畫板進行演示，從而驗證學生的想法。生5的想法如圖6所示。）

設計意圖：從單塊板的運動逐步提升到組合板的運動的過程中，學生需要掌握圖形的特征，平移、旋轉、軸對稱的特點，能夠簡潔地描述圖形的運動。在總分逐步減少的過程中，學生的空間觀念逐步發展。

（三）遷移經驗促融通

【教學片段8】

師：回看圖4-1和圖4-2，現在你認為⑦號板運動最低記幾分？

生： 1分。因為可以通過一次旋轉到達目標位置。

（教師利用幾何畫板顯示⑦號板的運動路徑，如圖7所示。）

師：大家重新思考一下，七巧板運動成小魚圖，每塊板的運動最低分是幾分？

……

設計意圖：七巧板運動分總分逐漸減少的過程，一次又一次地打破學生的思維定式，目光從部分到整體，旋轉中心從圖形中到圖形外，最后回頭看之前問題中⑦號板的運動，學生頓感“柳暗花明又一村”，思維的拔節清晰可見。

四、教學反思

在活動中，學生用語言描述圖形的拼擺，并結合幾何畫板進行操作，實現了語言和演示的同步性。根據學生對運動方式、路徑描述的不同，教師現場生成與語言描述相匹配的動態演示，以直觀的方式展示學生難以用語言描述或想象的運動路徑，促使學生建立豐富的表象。

幾何畫板具有強大的交互性和直觀性，它能夠不斷拓寬學生想象的空間，并提供可視化的動態表征，為學生的思維拔節提供了豐富的表象支持，幫助學生更好地理解和探索平面圖形的運動特性，培養學生的空間思維和創造力。