地形和風速影響下的海氣相互作用大渦模擬研究*

葉 燦 成澤毅 高 宇 宋金寶 李 爽

地形和風速影響下的海氣相互作用大渦模擬研究*

葉 燦 成澤毅 高 宇 宋金寶 李 爽①

(浙江大學海洋學院 浙江舟山 316021)

當水流經過海洋地形時, 水流的不穩定性會引起垂向混合并伴隨大量湍流過程。針對傳統海氣耦合模式缺少在湍流尺度上討論海洋地形與風速對海氣相互作用影響的問題, 使用并行大渦模擬海氣耦合模式(the parallelized large eddy simulation model, PALM)在5 m/s的背景風場下, 引入理想立方體地形, 對比有無地形的影響; 設置地形邊長為, 高為3(其中大氣部分高),與水深之比為/=1/2; 然后保持地形條件不變。設置5、10和15 m/s三種風速, 討論風速對小尺度海氣相互作用的影響。研究表明: 地形在大氣部分減弱順風向速度, 增強側風向速度, 影響0～5的高度區域, 而對垂向作用較小; 無地形條件下湍流垂向渦黏系數m在-0.3時, 水深達到最大值0.024 m2/s, 有地形條件下m在-0.8時, 達到最大值為0.16 m2/s, 地形的存在使得上層海洋混合加強,m最大值增加1個數量級。隨風速增大海洋和大氣中的凈熱通量、淡水通量和浮力通量都相應增大, 在近海面處, 5 m/s和10 m/s風速下三個通量的數值接近, 當風速為15 m/s時凈熱通量和淡水通量相較于前者數值大小增加2倍, 浮力通量增加近3倍, 說明大風加劇了各通量在海表的交換; 海洋混合層中湍動能收支各項也響應風速的變化, 其中剪切項、Stokes剪切、耗散項隨風速增大而增加, 且在區域-0.2～0變化明顯, 在近海表面處剪切項、傳輸項、壓力項和耗散項的值達到最大, 同時耗散項由傳輸項和剪切項平衡; 隨風速增大,m達到最大值的深度基本一致為-0.8。

大渦模擬; 地形與風速; 海氣通量; 湍流動能收支

海氣相互作用影響著海洋生態要素的空間分布, 是影響海洋生態系統的重要過程, 是當前海洋科學的研究熱點。而海洋上混合層作為一個中間層聯系起大氣底邊界層和上層海洋, 是海氣熱量通量和動量交換的重要界面, 對海洋上混合層的熱力學和動力學結構展開的研究已引起越來越多的關注(Phillips, 1980; Sullivan, 2010; Reichl, 2022; Gao, 2023; Jia, 2023)。湍流的生成及其垂向混合形成并維持了海洋上混合層, 作為中間層其同時受到多種時空尺度海洋和大氣運動過程的影響, 因此具有復雜的熱力學和動力學結構特征(吳凡, 2022; Pellichero, 2017; Von Storch, 2023)。同時海氣界面動量通量也稱為風應力, 是海流和表面海浪的主要驅動力, 是海洋從大氣獲得動量的重要途徑。

圍繞三維障礙物的湍流在自然界中很常見, 并出現在許多應用中。當水流經過三維障礙物時, 其不穩定性會導致在三維障礙物后方產生一系列中小尺度渦旋, 其中伴隨著大量的湍流過程。舟山群島是我國第一大群島, 也是重要的漁場, 其島嶼眾多, 水動力條件十分復雜(秦華偉等, 2014; 劉紫薇等, 2022), 影響漁場及其周圍生態。舟山市嵊泗縣海域目前擬投資建設中廣核嵊泗5#、6#海上風電場工程, 工程的建設會大大影響附近海域的水動力過程(Menéndez- Vicente, 2023; Syed, 2023)。了解和分析此類地形條件對海洋以及大氣的影響可以推動對海氣相互作用的相關研究。由于海洋條件的復雜危險性, 相關海洋數據十分不易獲得, 而且通常獲取的數據不夠詳細。高分辨率衛星觀測資料的大量增加為人們認識中緯度中小尺度的海氣相互作用提供了條件, 但存在分辨率不夠的問題, 研究表明分辨率低于1°的觀測數據對海洋鋒和海洋渦旋現象等描述不足, 嚴重低估了中小尺度上的感、潛熱通量變化, 進而可能低估了海表熱通量對熱帶外氣旋活動的影響(Rouault, 2003)。雖然觀測數據逐漸由單點向區域和全球尺度延展, 但是仍無法覆蓋全部(McClain, 2009), 同時也無法完整體現海洋現象的年代際變化等特征(Capotondi, 2015)。隨著超級計算機的出現, 利用數值模擬來研究這些相互作用已經成為可能。Walko等(1992)利用大渦模擬(large eddy simulation, LES)方法對比探究平坦地形和正弦丘陵地形之間可能存在的差異, 發現丘陵地形山頂附近上升運動的概率為70%, 山谷只有15%, 丘陵地形與平坦地形時變量的水平平均垂直廓線沒有重要差別, 但該研究忽略了水平風的影響。He等(1997)用大渦模擬方法研究了單個建筑物周圍的流場特征及建筑物頂部的渦旋結構。Shah等(1997)強調了大渦模擬方法用于立方體周圍流場模擬的重要性。Wood(2000)在復雜地形流場模擬的回顧與LES前景展望中指出, LES在復雜地形流場模擬方面有獨特的優越性, 但是也有很大的困難, 同時受計算量的限制。Gopalakrishnan等(2000)利用大渦模擬方法評估在哪些尺度上, 地形開始顯著影響對流邊界層(convective boundary layer, CBL)中湍流的平均特征和結構, 研究發現, 湍流與地形特征的尺度呈非線性關系。Lu等(2018)利用大渦模擬模式探究海底波狀地形上湍動能收支的情況, 但其使用的是單一海洋模式, 未考慮海洋與大氣之間的相互作用。李德順等(2021)以Risf實驗室開展的Bolund島實驗結果為依據, 采用雷諾時均與大渦模擬方法對Bolund島進行數值模擬, 將模擬區域方向坐標線為239°和270°的兩條特征線命名為Line A和Line B, 研究結果表明: 針對Bolund島的數值模擬, 在Line B特征線上5 m高度處模擬值比2 m高度處更接近實驗值, 在島前的位置模擬結果比島后更準確, 同時說明LES方法能夠有效揭示Bolund島地形周圍流動的繞流特征和尾流區渦特征。胡帥等(2021)考慮地形與風速的響應, 建立風速的空間相關性模型, 并將得到的風速數據轉換為風電功率數據。

大渦模擬耦合模式作為一個好的方法已經開始被廣泛應用于海洋和大氣之間小尺度相互作用的研究中。Esau(2014)將大渦模擬的海洋模塊與大氣模塊進行耦合, 探究了間接耦合機制在海氣相互作用中的重要影響, 但未考慮風的作用。Noh等(2004)和Li等(2013)將Langmuir環流效應和波浪破碎效應加入了湍流大渦模擬中, 使得湍流大渦模擬在海洋上層的模擬更加接近實際海況; 孫丹譯等(2020)使用大渦模擬海氣耦合模式, 探究風速對小尺度海氣相互作用的影響, 通過海氣通量以及湍流動能收支進行表征; 但都缺少對有地形海域條件的分析。為此本文在前人的研究基礎上使用并行大渦模擬海氣耦合模式(the parallelized large-eddy simulation model, PALM)進行數值模擬, 通過流場分布、海氣通量、湍流垂向渦黏系數和海洋湍流動能收支各項分布作為表征, 探究地形和風速對小尺度海氣相互作用過程的影響。

1 模式簡介及設置

1.1 PALM簡介

本研究使用的是基于Boussinesq近似的非流體靜力學數值模擬模式PALM, 對經過濾波的不可壓縮Navier-Stokes方程進行求解。其基本方程如下公式(1)～(4)所示。

其中, 等式中尖括號表示水平域平均值, 上劃線表示水平平均, 下標0表示海表面值, 雙撇表示次網格尺度湍流模式變量。

根據公式(1)～(4), 利用張量伸縮運算, 通過在時間差分之前將動量預算項乘以適當的擾動速度場, 推出空間水平平均的次網格湍動能方程(subgrid- scale tuebulence kinetic energy, SGS-TKE) (Skyllingstad, 2000):

公式(6)中等號右邊各項依次是: 速度剪切項、浮力項、次網格耗散項、湍流動能傳輸項、壓力項和耗散項。在表1中列舉出了上述方程中出現的所有參數及其說明。

表1 參數列表

Tab.1 List of parameters

1.2 海氣耦合模式簡介

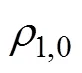
邊界條件如式(12)所示:

1.3 模式設置

本文使用PALM海氣耦合模式, 初始設置包括海洋和大氣兩個部分。考慮到在模式中加入理想立方體地形,為了保證在模擬水域內可以充分討論地形帶來的影響, 設置足夠大的模擬區域, 海洋部分網格數為640×320×100 ()個, 網格大小是1.25 m× 1.25 m× 1 m, 即模擬區域大小為800×400×100 m3(); 大氣部分的網格數是640×320×60 ()個, 網格大小是1.25 m×1.25 m×5 m, 即模擬區域大小為800×400× 300 m3()。PALM海氣耦合可以分為前驅運行和耦合運行兩個部分, 這兩個部分的各項初始條件設置大致相同, 采用三階Runge-Kutta方法為時間步長方案, 將側邊界條件設置為周期性邊界條件, 同時海洋模式中的上邊界和大氣模式中的下邊界均采用自由滑移邊界條件。參照Esau (2014)的相關研究內容設置大氣模式的表面溫度是270.6 K, 溫度梯度是0.015 K/m, 海洋模式溫度是272.65 K, 鹽度是34.8, 本文中緯度設置為45°N, 具體初始溫鹽剖面如圖1所示。

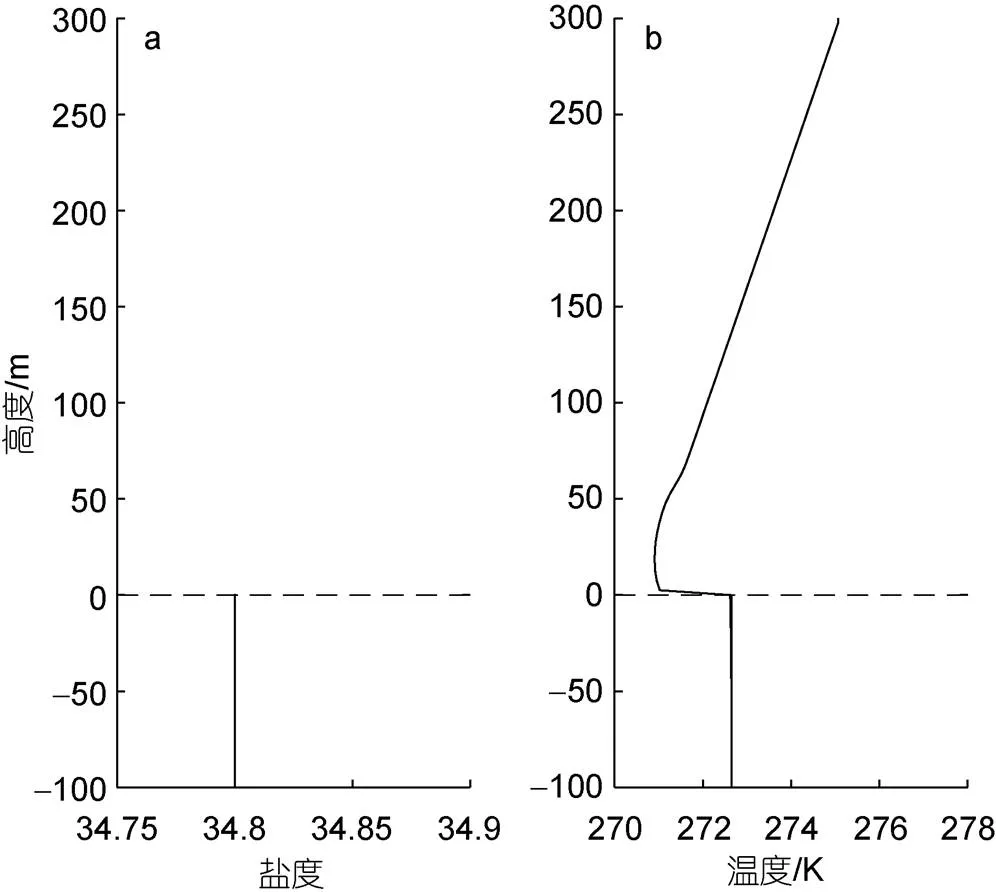
圖1 初始溫鹽剖面

注: a: 鹽度剖面; b: 溫度剖面

本文不考慮海洋分層和海洋背景流, 前驅運行時通過風速的輸入使大氣模式啟動, 在海洋初始運行時引入一個微小的擾動使得海洋模式啟動, 具體表現是輸入模式中在海表以熱通量形式加入, 模擬結果不會受該微小擾動所影響。前驅運行中設置運行時間大氣模式和海洋模式均為28 800 s, 耦合運行的時間則為86 400 s, 耦合的時間步長均是30 s。本文首先通過在5 m/s的地轉風背景下設置無立方體地形和有立方體地形兩種實驗來探究地形對流場分布、海氣通量及湍流垂向渦黏系數的影響, 將無地形條件命名為EXP_O, 有地形條件命名為EXP_T。具體對比實驗設置見表2所示。

表2 對比實驗設置1

Tab.2 Setting of the control experiment 1

注: EXP_O: 無地形條件; EXP_T: 有地形條件

探究地形對海氣相互作用的影響, 簡單起見, 本文在耦合模式中加入理想立方體地形(圖2), 以立方體柱的形式模擬三維地形的存在。定義理想立方體柱長、寬為, 高為3(其中在海洋部分高占2, 大氣部分高占), 模擬域總水深定義為,=2。然后不改變地形條件, 設置三種地轉風速度(5, 10和15 m/s)來討論改變風速對小尺度海氣相互作用的影響, 具體對比實驗設置見表3。

表3 對比實驗設置2

2 有無地形對小尺度海氣相互作用的影響

2.1 流場變化

首先關注大氣和海洋中速度分量在垂向上的變化, 將數據進行時間平均后得到大氣風速和海洋流速三個分量、和的垂向剖面圖(圖3)。圖3中橫坐標為速度大小, 黑線表示無地形條件EXP_O, 紅線表示有地形條件EXP_T。為了便于展示, 本文將海洋部分的速度分量、數值放大100倍。

與EXP_O相比, EXP_T中在地形的作用下, 大氣部分方向風速明顯減小, 模擬實驗中設置立方體地形長寬以及在大氣部分的高度相等, 與模擬域水深之比為/=1/2, 其對速度的影響高度可到5, 隨高度升高地形作用逐漸減弱, 風速有所回升, 并且在高度大于5后數值略大于無地形條件。海洋部分在海表面處EXP_T條件下速度最大為0.023 m/s, 相比于EXP_O條件最大值為0.045 m/s減小一半; 隨水深加深兩種實驗條件下速度分量數值相接近。由于模式的地轉風輸入只在水平方向, 所以在EXP_O中大氣側風向速度隨高度升高逐漸減小, 在高度大于5時趨向于0, 表明在5 m/s的風速作用下對側風向的作用同樣可達5的高度。在EXP_T中方向風速較之無地形情況下有所增大, 說明地形的存在可以降低順風向速度, 增加側風向速度。海洋部分海底方向流速從0開始變化且都為正值, 同一樣兩種實驗條件下數值也相近。速度分量在大氣部分兩種實驗條件下幾乎相同且接近零, 表示低風速影響下大氣垂向作用較弱, 值得注意的是, 在EXP_T中, 由于高1立方體地形的存在, 在地形頂部絕對值陡然反向增大然后恢復穩定變化趨勢。在海洋中, 地形阻擋作用使從總體上數值減小, 在海表由于地轉風的作用, 隨水深加深逐漸增大, 當能量向下傳遞至逐漸耗散,值開始減小直到遇到底邊界數值為0。

圖3 區域水平平均的速度剖面圖

注:為水深,為理想立方體長度; EXP_O: 無地形條件; EXP_T: 有地形條件; 背景風向沿水平方向

圖4和圖5分別展示了大氣部分在0.2高度處和海洋部分在-0.2深度處的瞬時大氣風速(海洋流速)、、的變化情況, 時間取模式最后輸出時刻, 用EXP_T減去EXP_O, 反映加入地形后流場的增減情況。圖中橫縱坐標將理想立方體地形存在的中間位置處數值設為0。在初始設置中緯度為45°N, 即科氏力,=10-4s-1由于Ekman-Stokes邊界層動力學的影響, 所以在圖4中可以看到大氣中的風向沿水平方向順時針偏轉。在地形斜后方水平距離4的區域內兩個實驗下風速分量和的差值為負, 因為在EXP_T中受地形影響, 在地形后方一塊區域的風速約為0, 所以速度分量差值為負。圖4c中在地形斜后方風場分量數值變化較為混亂, 表明此區域垂向混合劇烈。

同樣地, 受地形影響, 在其后方一塊區域的流速約為0, 被稱為“死水區”, 所以圖5a顯示在地形后方, EXP_T和EXP_O流速差值為負值, 圖中死水區的上下寬度和地形直徑大體一致, 且流速在縱向上(水平方向)向兩側方向增大, 一段距離后恢復正常, 在橫向上(水平方向)上約6處流速逐漸恢復正常, 但是受風和地形的持續影響, 之后的一段水流變得混亂。對速度分量的變化進行討論, 從圖5b中可以看出, 在地形前方產生兩股相反的水流, 是由于地形存在的繞流效應導致的偶極子型, 在地形前方兩端對稱。圖5c中, 速度分量在地形后方劇烈變化, 表示由于地形作用其后方垂向混合作用加強。

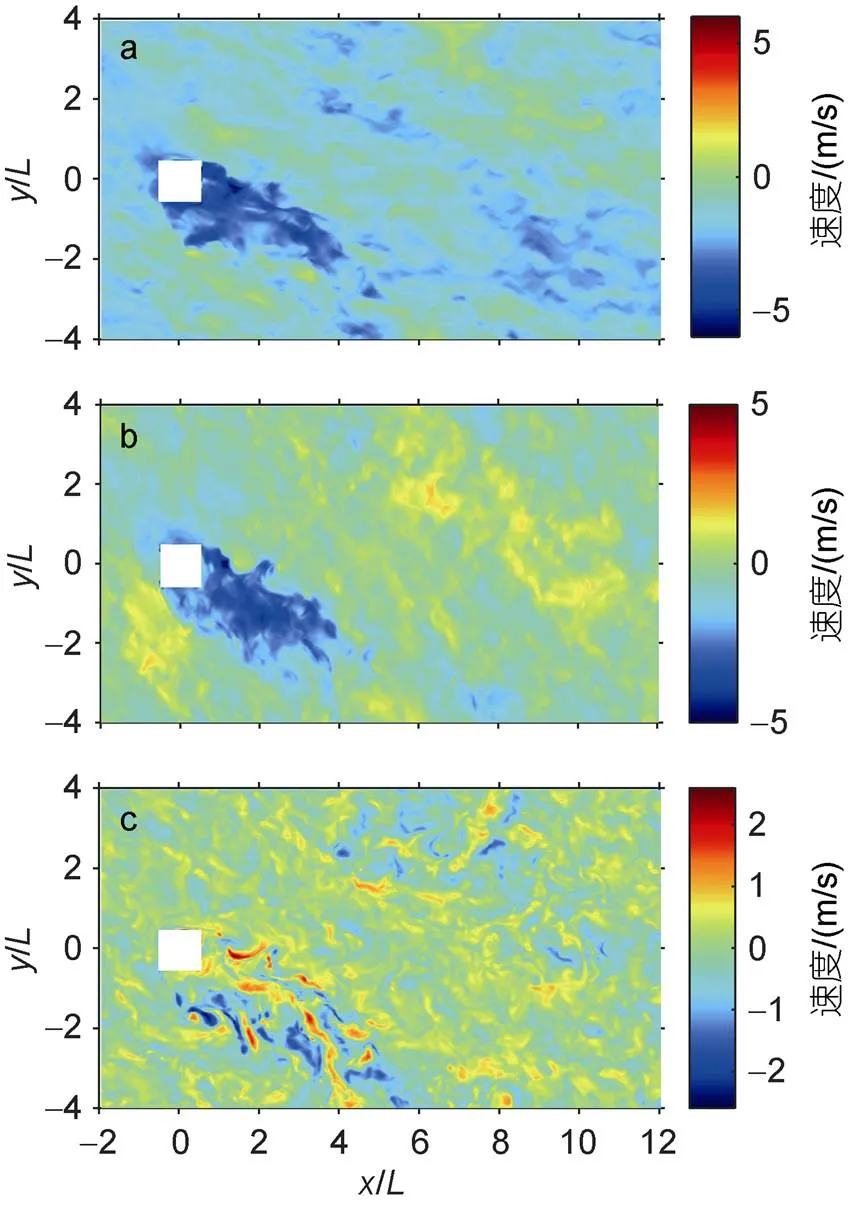
圖4 10 m高度瞬時風速圖(大氣部分)

注: a:; b:; c:; 空白方塊表示理想立方體地形

圖5 水下10 m瞬時流速圖(海洋部分)

注: a:; b:; c:; 空白方塊表示理想立方體地形

2.2 海氣通量

PALM中的海氣耦合是ABL和OML之間的耦合, 耦合是通過一個大氣-海洋界面來保存每個單元網格內的質量(濕度、鹽度)、動量和熱量的湍流通量。以ABL底部的湍流通量為OML的上邊界條件, 以OML頂部的速度和海表溫度作為ABL的下邊界條件。ABL在上一個時間步長獲得表面湍流通量(熱、動量、質量)用于設置OML頂部邊界, 在同一時間步長中, OML為下一個時間步長設置ABL底邊界的表面溫度和速度。

通過模式所得數據對其進行時間平均得到圖6, 圖中橫坐標為通量。由圖6可以直觀地看到兩個實驗下海氣通量的垂向變化。在海氣界面, 加入地形條件后, 大氣中的凈熱通量、淡水通量都相應增大, 在同一高度下有地形條件時凈熱通量、淡水通量要更大; 而浮力通量的數值在0～2.4的區域內大于無地形條件且為正值, 在2.4～5.0的區域內小于無地形條件且為負值, 在5～6的高度區域凈熱通量、淡水通量和浮力通量在兩個實驗條件下數值相近且趨向于0, 說明地形對大氣部分的影響高度在0～5, 這與圖3中對速度剖面進行分析得出的結果一致。

圖6 凈熱通量、淡水通量和浮力通量的垂向剖面圖

注: a: 大氣和海洋的凈熱通量; b: 大氣的淡水通量, 海洋中用鹽度通量代替; c: 大氣和海洋的浮力通量

海洋部分在加入地形條件后, 凈熱通量和浮力通量都減小。而淡水通量(在海洋中用鹽度通量代替)在-1～0的深度區域內未加入地形條件時為負值, 加入地形條件后為正值, 表明地形存在使海表面受熱蒸發減少; 在-2～-1的水深區域內則相反, 未加入地形條件下為正值且接近于0, 表明在水深到達-1直到海底蒸發很弱, 在加入地形條件后為負值, 地形的存在給水深-1到海底的區域內帶來一定的(熱量)鹽度交換。同時加入地形后, 各通量在海洋向下傳遞的距離和在大氣中向上傳遞的距離與在無地形條件下相差不大。

2.3 垂向渦黏系數

可通過湍流垂向渦黏系數來指示海洋的垂向混合過程。Boussinesq(1877)第一次提出關于湍流垂向渦黏度的假設, 其計算公式為

根據公式(13)計算得到海洋部分的垂向渦黏系數隨深度變化如圖7所示, 圖中橫坐標為湍流垂向渦黏系數m數值。因為本節模式設置風速輸入只沿水平方向, 所以只研究沿該方向上的m變化。模式基本達到穩定狀態的時間為運行開始后20 min, 因此取模式運行20 min后的水平平均值。

圖7 區域水平平均的垂向渦黏系數

從圖中可以看出, 在EXP_O垂向渦黏系數m的值在海表從0開始, 這是因為模式未考慮波浪破碎效應和海表通量的輸入等條件; 然后隨水深增大m的值逐漸增大, 當水深為-0.3時達到最大值, 為0.024 m2/s, 是由于表面風場的作用使得垂向混合加劇; 接下來由于風作用向下傳遞的能量逐漸耗散, 所剩余能量不足以維持水體的混合, 所以隨水深繼續增加m值開始減小。與EXP_O相比較, 在EXP_T中加入立方體地形后整體m值的變化趨勢保持不變, 即增大到最大值后再減小, 但在相同水深處m數值明顯增大, 其達到最大值的深度也有所加深為-0.8, 同時m最大值相比于EXP_O增加1個數量級, 為0.16 m2/s。說明在地形作用下, 海洋垂向混合增強。總體上m值均小于1, 根據公式(13)說明影響m變化的主要因素為垂向剪切。

3 有地形條件下風速對小尺度海氣相互作用的影響

3.1 垂向動能時間序列

本節保持1.3節的初始條件不變, 改變風速, 設置5、10、15 m/s三種不同地轉風速度, 在立方體地形存在條件下, 對不同風速下的小尺度海氣相互作用情況進行分析。

圖8展示了在不同風速下大氣和海洋部分的垂向動能時間序列, 圖中橫坐標為時間, 縱坐標為垂向動量通量, 為負值表示動量向下傳遞。從圖8中可以看出, 耦合模式下, 相較于海洋, 大氣部分可以更快達到穩定狀態, 在各風速下海洋模式約在3 h后均能達到穩定。大氣模式中, 隨風速增大動量在垂向上的傳遞逐漸加強, 在風速為5 m/s時, 對所有時間序列輸出的垂向動量通量數值進行平均, 得到其平均值為-2.2×10-2m2/s2; 風速為10 m/s和15 m/s時, 垂向動能值上下波動。海洋模式中, 垂向動能的變化并不完全響應風速的增大, 在不同風速下達到穩定狀態后其值上下波動變化。

圖8 垂向動能時間序列

注: a: 大氣的垂向動能; b: 海洋的垂向動能

3.2 流場分布

時間平均后得到大氣風速和海洋流速分量、、的垂向剖面如圖9所示, 圖中橫坐標為速度。圖9a顯示在大氣模式中, 同一風速下隨高度升高逐漸增大且增大趨勢隨高度上升漸緩, 同時隨風速增大逐漸增大。在圖9a海洋部分, 風對流速的作用在海表處較為明顯, 風速為5 m/s時, 海表最大值為0.023 m/s; 風速為10 m/s時, 海表最大值為0.044 m/s增大將近1倍; 風速為15 m/s時, 海表最大值為0.06 m/s。隨水深加深, 風給速度分量帶來的變化逐漸減小, 在不同風速條件下數值接近。圖9b大氣模式中, 速度分量在10和15 m/s的地轉風速下隨高度升高風速增大且增大趨勢逐漸變緩, 而在5 m/s風速下一開始隨高度升高緩慢增大, 在高度大于3L后又緩慢減小; 總體上隨初始地轉風風速增大逐漸增大, 說明在低風速下風的作用帶來的側風向速度增大效果沒有高風速下好。在海洋部分, 同一樣,在近海面處變化迅速, 不同的是在同一水深處隨風速增大數值呈較明顯的增大趨勢。

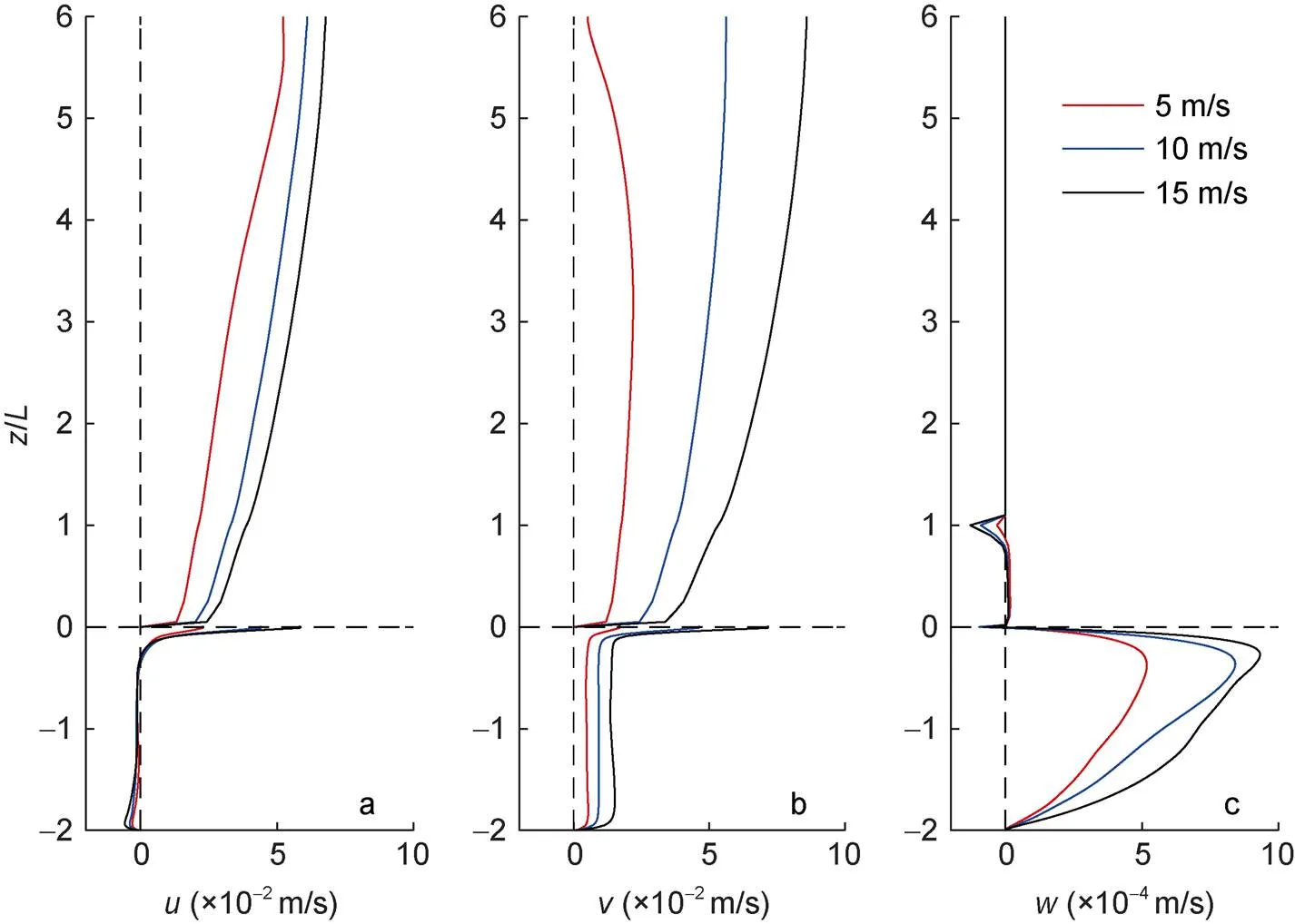
圖9 速度剖面圖

從圖9c中可以看出, 在大氣模式中垂向流速總體上變化不明顯, 但在高度為1處,值反向突增又迅速減小, 是由于大氣模式中1高的地形作用, 在地形頂部形成反向渦旋, 同時初始設置的地轉風速度越大,值突增越明顯, 說明在大風速作用下風和地形的相互影響更強。風應力可以使海洋表層產生水平流動, 從而破壞混合層的穩定性, 使混合層中的水體發生垂向運動, 因此海洋混合層中的垂向速度比海表處的垂向速度要大得多。在風速作用下隨水深增大逐漸增大, 在約-0.3處達到最大然后逐漸減小, 海底減至0, 說明風的作用深度大概為水下0.3。為了更清晰地展示流場變化, 取模式最后輸出時刻作出大氣模式0.2高度處和海洋模式-0.2深度處的瞬時水平流速圖(圖10), 用有地形條件的結果減去無地形條件的結果, 顯示加入立方體地形后流速的增減情況。隨風速增大, 大氣部分在地形右后方出現明顯的下降氣流, 且影響范圍逐漸增大, 當風速為15 m/s時, 影響可達地形后方3距離。海洋部分, 在風速為5 m/s時地形后方受到影響水流顯得混亂的距離約為6, 隨著風速的增大, 影響范圍也逐漸增大, 在整個模擬水域內水流變得混亂。

3.3 瞬時渦度

圖11為在不同風速下水下-0.2處的瞬時(模式最后輸出時刻)渦度水平截面圖, 圖中白色區域表示立方體地形, 灰色區域代表渦度值為0。從圖中可以看出在立方體地形后面形成大小近似相等方向相反的對稱渦結構, 其渦度數上半為負值, 下半為正值。當風速為5 m/s時, 在水平距離約為2.3處渦度上下分布慢慢匯合, 形成完整的“渦街”結構; 風速為10 m/s時, 上下分布的渦匯合距離變短, 約為2, 而風速為15 m/s時則在1.8處形成完整的“渦街”結構, 可見風的增加對尾渦有一定聚攏作用。不同風速下, 立方體地形后方尾部的渦結構相似, 渦在水平方向的移動范圍也很相近, 但當風速增大可以影響的水平距離更遠, 渦度分布也更為分散。

圖10 大氣和海洋部分速度w分量的水平截面

注: a～b: 5 m/s; c～d: 10 m/s; e～f: 15 m/s; 空白方塊表示理想立方體地形

圖11 不同風速下水下5 m瞬時渦度分布圖

注: a～b: 5 m/s; c～d: 10 m/s; e～f: 15 m/s; 空白方塊表示理想立方體地形

3.4 海氣通量

圖12展示了不同風速下海氣通量的垂向變化, 圖中橫坐標為通量大小。總體上來看, 大氣部分隨著高度升高各通量值逐漸減小; 在海氣界面處, 隨著風速的增大, 大氣中的凈熱通量、淡水通量和浮力通量也都相應增大; 圖12c中, 由于地形的存在, 在高度為1處浮力通量陡然減小再迅速恢復至正常變化趨勢, 且風速越大突變程度越大。

海洋中隨水深由淺至深凈熱通量、淡水通量和浮力通量逐漸增大, 且隨風速增大相同水深處各項通量值也相應增大, 在近海面處, 5和10 m/s地轉風條件下, 其凈熱通量、淡水通量和浮力通量數值接近, 而當風速為15 m/s時凈熱通量和淡水通量相較于前者數值大小增加2倍, 浮力通量增加近3倍, 說明大風加劇了各通量在海表處的交換。對不同條件下各通量向下傳遞的距離進行分析, 風速越大各通量值向下減小的趨勢越緩慢, 說明風速的增加會減緩各通量在海洋上層中的消耗, 這與孫丹譯等(2020)的研究結果相同。

圖12 凈熱通量、淡水通量和浮力通量的垂向剖面圖

注: a: 大氣和海洋的凈熱通量; b: 大氣的淡水通量, 海洋中用鹽度通量代替; c: 大氣和海洋的浮力通量

3.5 湍流動能收支

圖13是海洋部分在三種不同風速條件下的湍流動能收支圖, 根據公式(6)計算得出各項值, 圖中橫坐標為湍動能收支, 紅線代表速度剪切項, 天藍線代表Stokes剪切項, 綠線代表傳輸項, 藍線代表壓力項, 黑線代表耗散項, 為了便于展示將各項數值×106。左側圖為不同風速條件下海洋湍流動能收支情況, 右側均為左側在水深-0.4～0范圍的局部放大圖。

從圖13a、13c和13e中可以發現, 海洋湍流動能收支各項約在-0.2處迅速減小。在低風速條件下(即風速為5 m/s), 模式中地形的存在抑制了剪切項的生成, 所以剪切項數值較小, 在距離海面約-0.1～0范圍內剪切生成又迅速消失, 剪切項與耗散項在近海面處的值達到最大值且兩項大致持平, 最大值約為4.35×10-8m2/s3。耗散項表示摩擦引起的動能損失, 已有研究表明動量從近海表傳遞到整個海洋混合層, 大約有40%的輸入能量通過湍流耗散損失(Skyllingstad, 2000)。剪切和耗散之間在近海面處的近乎平衡表明, 大部分的湍流能量集中在直接受次網格耗散影響的小規模流動特征中。當風速增大至15 m/s時, 剪切項明顯增大, 地形抑制作用減弱, 其最大值為8×10-7m2/s3。海洋混合層中湍流動能收支也響應風速的變化, 其中剪切項、Stokes剪切、耗散項隨著風速增大而增加, 且在區域-0.2～0變化明顯, 由于海洋模式受到大氣風速的驅動, 所以在近海表面處各項值都達到最大, 之后隨深度增加逐漸減弱。同時在上層海洋中耗散項通過傳輸項和剪切項來平衡。

3.6 垂向渦黏系數

根據公式(13)計算得到海洋部分的垂向渦黏系數隨深度變化如圖14所示, 圖中橫坐標為湍流垂向渦黏系數。同2.3節一樣, 本節模式風速輸入只有水平方向, 所以只研究沿水平方向的m變化, 取模式運行20 min后的水平平均值。

從圖14中可以看出,m的垂向分布趨勢受風速影響, 呈現先增大后減小的趨勢。對比不同風速條件可以看出, 隨著風速的增大, 總體上在相同水深m值也增大; 當風速為15 m/s時,m最大值可達0.33 m2/s, 相較于風速為5 m/s時數值增大1倍。但是, 風速不同m值達到最大值的深度基本一致, 這與通過MY2.5等模式所得出來的結果有出入, 之前的結果顯示風速越大m最大值的出現位置越向水域更深處移動(Furuichi, 2015), 但是在實驗室實驗以及數值模擬中有被捕捉到類似的結論。陸宗澤(2018)將MY2.5垂向湍流參數化的結果與湍流大渦模擬的結果進行了對比, 結果發現, 大渦模擬的結果和MY2.5的結果吻合得很好, 并且大渦模擬在湍動方面體現得更好, 大渦模擬區別于傳統的垂向混合參數化方案, 直接計算出垂向湍流渦黏系數。文章設置4組不同的海表面10 m風速(10、15、20、25 m/s), 結果表明隨風速增大垂向渦黏系數m達到最大值幾乎保持在一個深度。同時m值均小于1, 在不同風速條件下垂向剪切依舊是影響m變化的主要因素。

圖13 不同風速下的湍流動能收支圖

注: a: 5 m/s, b: a的部分放大圖; c: 10 m/s, d: c的部分放大圖; e: 15 m/s, f: d的部分放大圖

圖14 不同風速下垂向渦黏系數剖面

4 結論與展望

本文通過大渦模擬海氣耦合模式來探究地形和風速對小尺度海氣相互作用的影響, 設置理想立方體地形, 地形長寬為, 高為3(其中大氣部分高), 與水深之比為/=1/2, 在5 m/s背景風下, 對比有無地形的區別, 然后保持地形條件不變, 改變風速為5、10和15 m/s, 展示不同風速下大氣風場和海洋流場、海氣通量以及海洋混合層湍動能收支各項的分布。主要結論如下:

(1) 地形在大氣部分減弱順風向風速, 增強側風向風速, 作用高度在0～5的區域, 對垂向影響很小。在地形斜后方一小塊區域風速分量和減小為0,分量數值變化較為混亂, 表明垂向混合劇烈。在海洋部分水平流速變化不大, 在地形后面的一塊區域出現“死水區”, 在橫向上流速影響距離約6。在海氣界面, 加入地形條件后, 大氣中的凈熱通量、淡水通量都相應增大, 海洋中則是凈熱通量和浮力通量減小, 淡水通量(用鹽度通量表示)為正表明海面蒸發減少。同時相比于無地形條件下, 在有地形時m最大值增加1個數量級, 說明地形的存在使上層海洋混合加強。

(2) 隨著風速的增加, 在大氣部分, 垂向動能的分布呈現縱向加深的趨勢, 水體混合程度加深; 在海氣界面處, 隨風速增大大氣中的凈熱通量、淡水通量和浮力通量相應增大, 由于地形存在, 在高度為1處浮力通量陡然減小后恢復正常變化趨勢; 海洋中隨水深由淺至深凈熱通量、淡水通量和浮力通量逐漸增大, 且隨風速增大各項值也相應增大, 但在近海面處, 5和10 m/s地轉風條件下, 其三個通量的數值接近, 當風速為15 m/s時凈熱通量和淡水通量相較于前者數值大小增加2倍, 浮力通量增加近3倍, 大風條件下加劇了各通量在海表的交換; 海洋混合層中湍流動能收支也響應風速的變化, 其中剪切項、Stokes剪切、耗散項隨著風速增大而增加, 在區域-0.2～0變化明顯, 由于海洋模式受到大氣風速的驅動, 所以在近海表面處幾項值達到最大, 之后隨深度增加逐漸減弱。同時在上層海洋傳輸項和剪切項來平衡耗散項。隨著風速的增大, 總體上m值也增大, 風速為15 m/s時m最大值為0.33 m2/s, 是風速為5 m/s條件下m最大值的兩倍。風速不同m值達到最大值的深度基本一致, 為-0.8。

本文實現了基于大渦模擬的海氣耦合模式, 對于海洋和大氣之間通量交換等相互作用過程的研究有重要的參考意義。使用耦合模式充分考慮海洋部分與大氣部分的協同作用, 探究地形與風速的影響, 模擬結果與真實情況更接近, 從而為真實海洋中島嶼存在處的海洋動力研究以及風電場等工程建設過程提供指導。但海洋混合層受風速影響存在兩個重要湍流過程: 波浪破碎和Langmuir環流。波浪破碎在海面附近產生大量的小尺度湍流, 而由風驅動的表面流切變與Stokes漂移的相互作用產生Langmuir環流, 這兩者對于海洋混合層有較大影響。Noh等(2004)對海洋混合層進行了波浪破碎和Langmuir環流的大渦模擬, 揭示了波浪破碎和Langmuir環流在海洋混合層垂向混合過程中的重要作用。Li等(2013)使用大渦模擬研究兩者在海表邊界層中產生湍流的作用, 模式結果與從CBLAST站點湍流測量分析得出的結論一致。波浪破碎與Langmuir環流均發生在海氣邊界上, 影響海氣通量交換, 所以未來的工作重點便是在耦合模式中加入波浪破碎和Langmuir環流, 考慮二者對海氣相互作用的影響。

孫丹譯, 李爽, 2020. 基于大渦模擬耦合模式的小尺度海氣相互作用研究[J]. 海洋與湖沼, 51(6): 1310-1319.

劉紫薇, 趙帥康, 魏笑然, 等, 2022. 主流海表風場資料在舟山群島近海的性能評估[J]. 海洋與湖沼, 53(3): 528-537.

李德順, 董彥斌, 傅學剛, 等, 2021. Bolund島對風場流動影響的數值模擬研究[J]. 液壓氣動與密封, 41(5): 6-9.

吳凡, 2022. 南海上混合層結構表征[D]. 連云港: 江蘇海洋大學: 1-2.

陸宗澤, 2018. 風應力對海洋上層垂向混合影響的湍流大渦模擬[D]. 杭州: 浙江大學: 33-34.

胡帥, 向月, 沈曉東, 等, 2021. 計及氣象因素和風速空間相關性的風電功率預測模型[J]. 電力系統自動化, 45(7): 28-36.

秦華偉, 蔡真, 周紅偉, 等, 2014. 舟山特定海域三維水流數值模擬研究[J]. 機電工程, 31(4): 541-544.

BOUSSINESQ J, 1877. Essai sur la théorie des eaux courantes[M]. Paris: Imprimerie nationale, 663-666.

CAPOTONDI A, WITTENBERG A T, NEWMAN M,, 2015. Understanding ENSO diversity [J]. Bulletin of the American Meteorological Society, 96(6): 921-938, doi: 10.1175/ BAMS-D-13-00117.1.

ESAU I, 2014. Indirect air–sea interactions simulated with a coupled turbulence-resolving model [J]. Ocean Dynamics, 64(5): 689-705.

FURUICHI N, HIBIYA T, 2015. Assessment of the upper-ocean mixed layer parameterizations using a large eddy simulation model [J]. Journal of Geophysical Research: Oceans, 120(3): 2350-2369, doi: 10.1002/2014JC010665.

GAO Z, LONG S M, SHI J R,, 2023. Indian Ocean mixed layer depth changes under global warming [J]. Frontiers in Climate, 5: 1112713, doi: 10.3389/fclim.2023.1112713.

GOPALAKRISHNAN S G, ROY S B, AVISSAR R, 2000. An evaluation of the scale at which topographical features affect the convective boundary layer using large eddy simulations [J]. Journal of the Atmospheric Sciences, 57(2): 334-351, doi: 10.1175/1520-0469(2000)057<0334:AEOTSA>2.0.CO;2.

HE J M, SONG C C S, 1997. A numerical study of wind flow around the TTU building and the roof corner vortex [J]. Journal of Wind Engineering and Industrial Aerodynamics, 67/68: 547-558, doi: 10.1016/S0167-6105(97)00099-8.

JIA W T, SUN J L, ZHANG W M,, 2023. The effect of boreal summer intraseasonal oscillation on mixed layer and upper ocean temperature over the South China Sea [J]. Journal of Ocean University of China, 22(2): 285-296.

LARGE W G, MCWILLIAMS J C, DONEY S C, 1994. Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization [J]. Reviews of Geophysics, 32(4): 363-403, doi: 10.1029/94RG01872.

LI S, LI M, GERBI G P,, 2013. Roles of breaking waves and Langmuir circulation in the surface boundary layer of a coastal ocean [J]. Journal of Geophysical Research: Oceans, 118(10): 5173-5187, doi: 10.1002/jgrc.20387.

LU Z Z, FAN W, LI S,, 2018. Large-eddy simulation of the influence of a wavy lower boundary on the turbulence kinetic energy budget redistribution [J]. Journal of Oceanology and Limnology, 36(4): 1178-1188.

MCCLAIN C R, 2009. A decade of satellite ocean color observations [J]. Annual Review of Marine Science, 1: 19-42, doi: 10.1146/annurev.marine.010908.163650.

MELLOR G L, YAMADA T, 1982. Development of a turbulence closure model for geophysical fluid problems [J]. Reviews of Geophysics, 20(4): 851-875, doi: 10.1029/RG020i004p00851.

MENéNDEZ-VICENTE C, LóPEZ-QUEROL S, BHATTACHARYA S,, 2023. Numerical study on the effects of scour on monopile foundations for offshore wind turbines: the case of Robin Rigg wind farm [J]. Soil Dynamics and Earthquake Engineering, 167: 107803, doi: 10.1016/j.soildyn.2023. 107803.

NOH Y, MIN H S, RAASCH S, 2004. Large eddy simulation of the ocean mixed layer: the effects of wave breaking and Langmuir circulation [J]. Journal of Physical Oceanography, 34(4): 720-735, doi: 10.1175/1520-0485(2004)034<0720: LESOTO>2.0.CO;2.

PELLICHERO V, SALLéE J B, SCHMIDTKO S,, 2017. The ocean mixed layer under Southern Ocean sea-ice: seasonal cycle and forcing [J]. Journal of Geophysical Research: Oceans, 122(2): 1608-1633, doi: 10.1002/ 2016JC011970.

PHILLIPS O M, 1980. The Dynamics of the Upper Ocean [M]. 2nd ed. Cambridge: Cambridge University Press, 331-332.

REICHL B G, ADCROFT A, GRIFFIES S M,, 2022. A potential energy analysis of ocean surface mixed layers [J]. Journal of Geophysical Research: Oceans, 127(7): e2021JC018140, doi: 10.1029/2021JC018140.

ROUAULT M, REASON C J C, LUTJEHARMS J R E,, 2003. Underestimation of latent and sensible heat fluxes above the Agulhas Current in NCEP and ECMWF analyses [J]. Journal of Climate, 16(4): 776-782, doi: 10.1175/1520- 0442(2003)016<0776:UOLASH>2.0.CO;2.

SHAH K B, FERZIGER J H, 1997. A fluid mechanicians view of wind engineering: large eddy simulation of flow past a cubic obstacle [J]. Journal of Wind Engineering and Industrial Aerodynamics, 67/68: 211-224, doi: 10.1016/S0167-6105 (97)00074-3.

SKYLLINGSTAD E D, SMYTH W D, CRAWFORD G B, 2000. Resonant wind-driven mixing in the ocean boundary layer [J]. Journal of Physical Oceanography, 30(8): 1866-1890, doi: 10.1175/1520-0485(2000)030<1866:RWDMIT>2.0.CO;2.

STEINHORN I, 1991. Salt flux and evaporation [J]. Journal of Physical Oceanography, 21(11): 1681-1683, doi: 10.1175/ 1520-0485(1991)021<1681:SFAE>2.0.CO;2.

SULLIVAN P P, MCWILLIAMS J C, 2010. Dynamics of winds and currents coupled to surface waves [J]. Annual Review of Fluid Mechanics, 42(1): 19-42, doi: 10.1146/annurev- fluid-121108-145541.

SYED A H, MANN J, PLATIS A,, 2023. Turbulence structures and entrainment length scales in large offshore wind farms [J]. Wind Energy Science, 8: 125-139, doi: 10. 5194/wes-8-125-2023.

UMLAUF L, BURCHARD H, 2003. A generic length-scale equation for geophysical turbulence models [J]. Journal of MarineResearch, 61(2): 235-265, doi: 10.1357/002224003322005087.

VON STORCH J S, LüSCHOW V, 2023. Wind power input to ocean near-inertial waves diagnosed from a 5-km global coupled atmosphere-ocean general circulation model [J]. Journal of Geophysical Research: Oceans, 128(2): e2022JC019111, doi: 10.1029/2022JC019111.

WALKO R L, COTTON W R, PIELKE R A, 1992. Large-eddy simulations of the effects of hilly terrain on the convective boundary layer [J]. Boundary-Layer Meteorology, 58(1/2): 133-150.

WILCOX D C, 1988. Reassessment of the scale-determining equation for advanced turbulence models [J]. AIAA Journal, 26(11): 1299-1310, doi: 10.2514/3.10041.

WOOD N, 2000. Wind flow over complex terrain: a historical perspective and the prospect for large-eddy modelling [J]. Boundary-Layer Meteorology, 96(1/2): 11-32.

LARGE EDDY SIMULATION OF AIR-SEA INTERACTION UNDER THE INFLUENCE OF TOPOGRAPHY AND WIND SPEED

YE Can, CHENG Ze-Yi, GAO Yu, SONG Jin-Bao, LI Shuang

(Ocean College, Zhejiang University, Zhoushan 316021, China)

When water flows through ocean terrain, vertical mixing and a large amount of turbulent may occur due to water flow instability. Aiming at the issue that the traditional air-sea coupling model lacks of discussing the impact of ocean topography and wind speed on air-sea interaction on turbulent scale, the Parallelized Large Eddy Simulation Model (PALM) was used to introduce an ideal cube topography under background wind field of 5 m/s. The impact of topography was simulated under three wind speeds of 5, 10, and 15 m/s. In the simulation, the side length of the cube was 1L and the height was 3of which the height above water surface was 1, and the ratio ofand water depthwas 1/2. The impact of wind speed on small-scale air-sea interactions was discussed. Results show that topography could weaken the downwind velocity in the atmosphere, enhances the crosswind velocity, and affect the altitude range of 0～5, while the impact on the vertical direction is small. Under no-topography conditions, the turbulent vertical eddy viscosity coefficientmreached the maximum value of 0.024 m2/s at-0.3water depth without topography, while the maximum value of 0.16 m2/s at-0.8with topography. The presence of topography enhanced the mixing of the upper ocean and increased the maximum value ofmby one order of magnitude. As the wind speed increases, all the net heat flux, freshwater flux, and buoyancy flux in the ocean and atmosphere increased accordingly. At near the sea surface level, the values of the three fluxes under 5 m/s and 10 m/s wind speeds are similar, while at 15 m/s, the net heat flux and freshwater flux increased by two times compared to the former, and the buoyancy flux increased by nearly three times, indicating that strong winds could intensify the exchange of various fluxes at the sea surface. In addition, the turbulent kinetic energy budget in the mixed layer of the ocean responded to the changes of wind speed. The shear term, the Stokes shear term, and the dissipation term increased with the wind speed increase. The variation was significant in the region of-0.2～0, and the values of shear term, transmission term, pressure term and dissipation term reached the maximum near the sea surface. Meanwhile, the dissipation term was balanced by the transfer term and shear term. As the wind speed increased, the depth at whichmreached its maximum value was-0.8in overall.

large eddy simulation; topography and wind speed; air-sea flux; turbulent kinetic energy budget

* 國家自然科學基金項目，41830533號, 41876003號。葉 燦，碩士研究生, E-mail: yecan@zju.edu.cn

李 爽, 博士生導師, 副教授, E-mail: lshuang@zju.edu.cn

2023-04-23,

2023-06-20

P731.26

10.11693/hyhz20230400090