一道“弦圖”結構的中考題的分析與挖掘

張希

摘 要：本文對一道內涵豐富、蘊含數學文化的中考題進行多視角分析，理清幾何結構^［1］與代數表達之間的關聯，得到多種解法； 通過母題開發，得到系列好題.在解題教學中，不僅提高學生的解題能力^［2］，還促進幾何直觀、推理能力、運算能力等核心素養的發展，向學生滲透中華民族優秀傳統數學文化.

關鍵詞：數學文化；幾何結構;代數表達;解題教學;核心素養

1 “弦圖”溯源

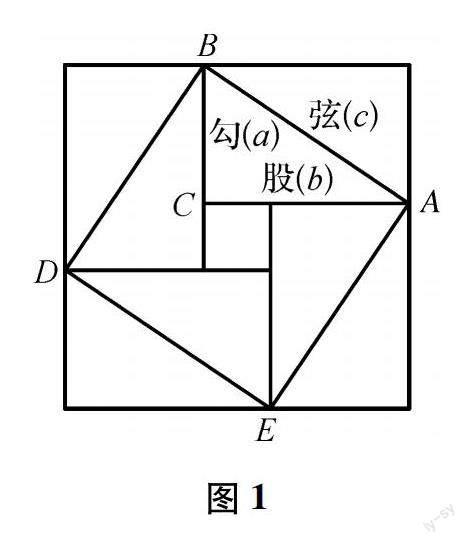
我國古代數學家趙爽在他創制的“勾股圓方圖”中，利用圖1，通過數形結合，給出了勾股定理的詳細證明.后人稱之為“趙爽弦圖”.這是眾多證明勾股定理的方法中最簡潔、最巧妙的.

趙爽的證明方法實現了“勾股定理”的一般化，其證明過程有圖為證，用幾何圖形的截、割、拼、補來證明代數式之間的恒等關系，既具嚴密性，又具直觀性.趙爽證明勾股定理的方法將代數和幾何緊密結合，使之互不可分，該證明方法被哈佛大學教授庫里奇稱為“最省力的證明”.因此，“趙爽弦圖”被選為2002年國際數學家大會會徽，現在這個標志也成了中國數學會的標志.

《普通高中數學課程標準（2017年版）》^［3］把“體現數學的文化價值”作為一條課程的基本理念，并具體指出：通過生動、豐富的事例，了解數學發展過程中若干重要事件、重要人物與重要成果，初步了解數學產生與發展的過程，體會數學對人類文明發展的作用，加深對數學的理解.

由此可見，勾股弦圖作為一種初中重要的數學文化，應當要充分發揮其價值.而勾股弦圖又是一種解決特定結構的數學問題的模型，是一種數學的思想方法，有助于發展學生運算能力、抽象能力和推理能力，這是《標準（2022版）》^［4］的重要要求，也是教材引入趙爽弦圖的意圖和價值.

正因如此，“趙爽弦圖”近年來已成為各地中考取材的熱點.本文通過分析和挖掘2023年杭州市中考數學第10題，得到多種解法與系列好題，從而向學生滲透中華民族優秀傳統數學文化.

2 原題呈現

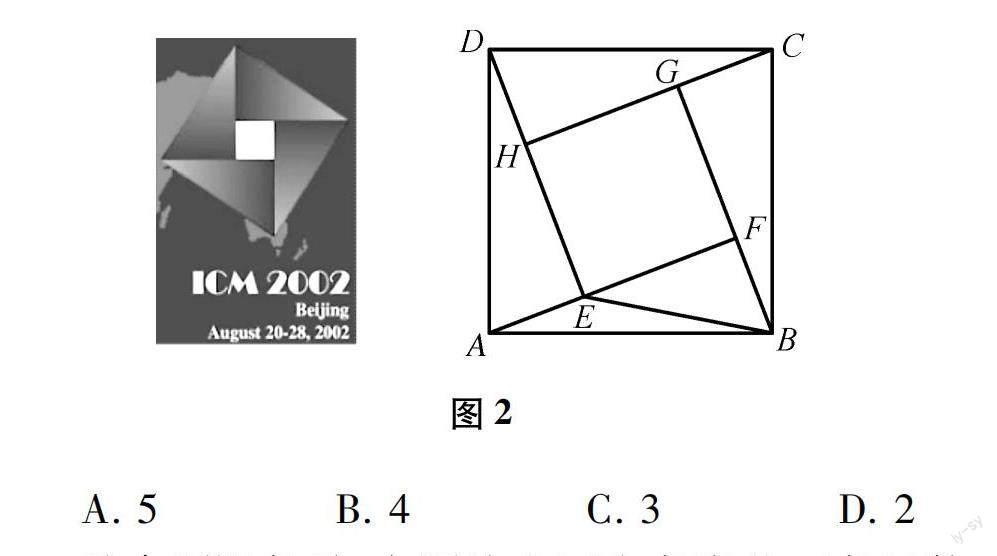
第二十四屆國際數學家大會會徽的設計基礎是1700多年前中國古代數學家趙爽的“弦圖”.如圖2，在由四個全等的直角三角形（△DAE，△ABF，△BCG，△CDH）和中間一個小正方形EFGH拼成的大正方形ABCD中，∠ABF＞∠BAF，連接BE.設∠BAF＝α，∠BEF＝β，若正方形EFGH與正方形ABCD的面積之比為1∶n，tanα＝tan²β，求n.

A. 5B. 4C. 3D. 2

從命題視角看，本題給出兩個角度的三角函數關系，進而求解兩個正方形的面積之比.本題體現“弘揚數學文化，彰顯育人價值”的理念，融代數、幾何、三角函數于一題的命題導向；涵蓋三角形全等、勾股定理、黃金分割、三角函數、圖形面積等知識；考查學生的閱讀能力，文字語言轉換成符號語言與圖形語言的能力，考查學生的構圖能力、運算求解能力、推理論證能力；探索了數量關系的不變性，從中歸納出代數表達；也考查了化歸與轉化思想、數形結合思想等.

3 解法展示

從圖形結構看，2023年杭州市中考數學第10題有“弦圖”結構.從解題思路上看，要求n的值，常見的思路是對三角形邊長設元，表示α與β的正切值，利用正方形的面積比值，列出等量關系求解.從已知條件出發設元列式，通過代數推理求解.因為本題也有特殊的數量關系，故還可以用華羅庚的優選法黃金比求解.

本題通過設元將所求問題與黃金分割、三角函數等知識聯系起來，培養學生多種途徑分析問題、解決問題的能力，體現了解決問題方法的多樣性.如何在復雜圖形中識別基本圖形以及圖形的幾何結構，抽出關鍵圖形，轉化為熟悉結構，如何構建幾何結構與代數表達之間的關聯，尋找通性通法，獲得解題思路是本題的難點.在此過程中，促進了學生幾何直觀、推理能力、運算能力等核心素養的發展.

4 試題開發

2023年杭州市中考數學第10題的結構特征、解題方法具有代表性和可衍生性.我們開發系列子題，這也是解題教學中提高教學效率的重要途徑，使學生靈活應用原題中的幾何結構與代數表達之間的關聯，解決新問題.下面是由原題開發的系列新題.

通過對母題的改編，改變題干條件，進而得到不同的設問：求三角函數值，求面積，求面積比、線段長、線段比等數量關系.上述變式從不同路徑衍生得到不同子題，但又緊密圍繞“弦圖”的結構，緊扣“設元列式，代數推理”或“借助黃金比，以算代證”的方法.

在研究變式的過程中，教師應當引導學生再與母題的解決方法進行比較，探索其本質；引導學生明白其中相同的原理，抓住“弦圖”結構帶來的代數表達的“不變性”.在探索系列題和衍生題時，使得學生深刻理解其中蘊含的數學方法與解題原理，學會舉一反三解決新問題；系列題教學研究深入、高效，有利于提高學生解題能力；讓學生明白只要改變題干，改變求證，就能得到千千萬萬的題目，但無論如何改變，不變的是問題的本質，這就是萬變不離其宗.

5 結束語

本文所列舉的試題與變式均以“趙爽弦圖”為背景，真正做到了將數學文化滲入了中考.“弦圖”結構的問題實際上是一種解決特定結構的數學問題的模型，是一種數學的思想方法.“弦圖”結構的問題讓學生經歷將復雜幾何問題“代數化”的過程，探索數量關系的不變性，不僅提升了運算能力、推理能力，也鍛煉了化歸思想、數形結合思想，這是《標準（2022版）》的重要要求，也是安排2023年杭州市中考數學第10題的意圖和價值.

中考試卷中數學文化試題不斷涌現.為響應學科育人的號召，廣大一線教師應當發揮中考試題的引領和導向作用，借助《九章算術》《周髀算經》《幾何原本》等著作，將數學文化真正滲入教材、融入教學，不但可使學生理解數學、喜愛數學，還可以激發學生的愛國熱情和學習激情，真正達成“情感教育”與考試功能的有機結合，力爭做到“文化搭臺，學生唱戲，教師喝彩”.

參考文獻：

［1］ 王紅權.聯系促進理解 結構揭示本質——一個平面幾何習題的拓展性教學研究［J］.中學教研（數學），2021（10）：19-22.

［2］ 傅蘭英.一道中考幾何壓軸題的解法分析與推廣［J］.中學教研（數學），2022（10）：42-45.

［3］ 中華人民共和國教育部.普通高中數學課程標準 （實驗）［M］.北京：人民教育出版社.2017.

［4］ 中華人民共和國教育部.全日制義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.