利用“問題”引導學生探究

韓生金

摘 要： 問題是思維的源泉.在新課改背景下，數學教師應堅持以問題引領為導向，不斷創新教學方式，調動學生參與熱情，構建新型數學課堂.教學中應善于借助問題來啟發學生思維，引導學生深入探究，最終讓學生自主構建數學知識體系，養成良好的學習習慣.

關鍵詞： 問題；數學教學；問題情境

在新高考背景下，教師要更加關注學生的數學核心素養，指導學生學以致用.而利用數學問題就是開拓學生思路、引導學生探究、發展學生素養的重要方法.在數學課堂上，如何靈活運用問題，激發學生的求知欲，張揚學生個性，是每一個數學教師應該思考的問題.但是在實際教學過程中，有時候教師設計的問題是低效的或者無效的，這樣會直接影響教學效果，需要在今后的工作中進行優化和調整.所以，高中數學教師要具備良好的教學思維，將問題導學落實到數學課堂的各個角落.一方面引發學生思考和嘗試，靈活運用所學數學知識；另一方面增強師生課堂互動，有利于實現學習共同體的構建.本文以“圓的標準方程”為例，先分析“問題”探究在高中數學教學中的作用，再論述利用“問題”引導學生探究的具體策略，旨在構建高效數學課堂.

1 “問題”探究在高中數學教學中的作用

1.1 提升數學學習水平

在實際教學中發現，有些高中生對于數學教師存在過度的依賴，只要是教師講解的內容都不會進行質疑，教師不講的內容也不會進行主動的復習，這樣就使學生的學習出現了斷層.如今，數學教師在課堂上設計出各種各樣的問題，一方面啟發學生進行深度思考，透過數學現象看本質，另一方面活躍課堂氛圍，提升學生數學學習水平.數學教師還可以將解題方法和學習理念等融入到問題中，營造一個輕松、高效的課堂氛圍，使學生帶著疑問積極投入到數學課堂中，加深對數學知識的理解和記憶.

1.2 推動課程改革深入

傳統灌輸式的教學方式存在著弊端，把學生的思維束縛在課本上，學生的主體性難以發揮.在新課改背景下，對高中數學教學提出了更多的要求，教師要引導學生自主學習，促使其發展.在這個過程中，學生的思維能力會得到提高，并且會形成數學應用意識.所以，越來越多的數學教師會在課堂上創設不同的問題，引導學生進行探究，以此達到教學目的，促使學生在探究中了解數學知識的形成過程，提供充足的數學食糧.學生結合問題學習數學知識，既可以完善自己的知識體系，又能加強對知識的了解，有利于改變傳統教學格局，實現數學教學改革.

1.3 增強師生互動效果

受到應試思想的影響，有些數學教師仍然把控整節課堂，對學生發號施令，沒有考慮到學生的學習感受，使得數學課堂枯燥又乏味，師生缺乏溝通和互動.然而，當數學教師將數學問題融入到課前、課中和課后時，學生對問題的判斷力和想象力會得到顯著的提升，固化的思維模式在逐漸消退， 與教師的互動效果也越來越好.尤其是隨著信息技術的發展，教師通過人工智能來進行課堂提問，讓學生對數學問題產生濃厚的興趣，及時向教師提出自己的疑問，在與教師的互動中實現深度學習，強化學生的信息素養.

2 利用“問題”引導學生探究的具體策略

2.1 營造和諧氛圍，讓學生敢問

不懷疑，就不能見真理，沒有疑問的教學，在學生的內心里就不會留下深刻的痕跡.在數學教學上，教師應巧妙運用問題，營造和諧的課堂氛圍，將學生的注意力牢牢吸引到課堂上，并充分發揮學生的主體作用，鼓勵他們向教師提問，從而獲得最大程度的進步.教師還要一視同仁，對于學生提出的千奇百怪的問題都要給予鼓勵，使他們的探索欲和好奇心在廣闊的平臺上得到鍛煉，在數學學習上呈現出百花齊放的態勢，實現核心素養的有效落實.

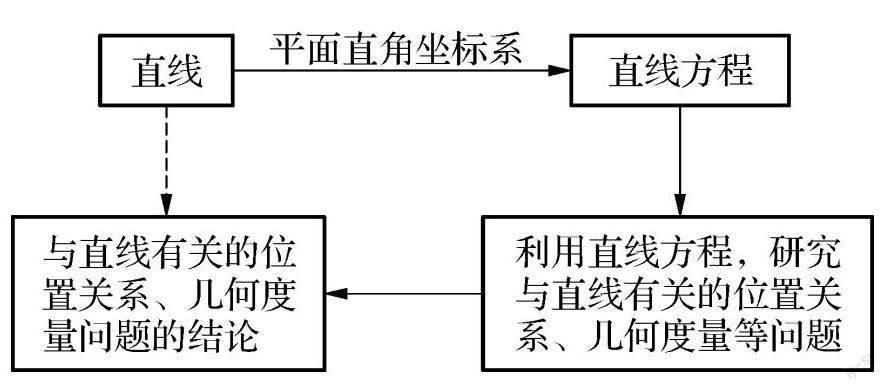
例如，講高中數學“圓的標準方程”，教師會引導學生自主探究，引導他們結合教材內容找到論證“圓的標準方程”的方法，并學會靈活應用相關知識，鍛煉邏輯推理能力和數學實踐能力.在課程導入的時候，教師通過平面直角坐標系的方法表示點和直線，最終推導出直線的方程，還給出了直線與方程的簡易思維導圖（如下圖）.

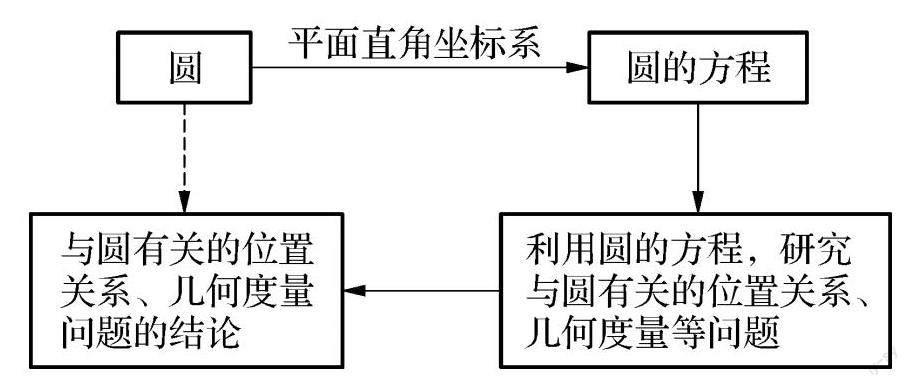
然后教師順勢提問：請同學們思考，能不能在平面直角坐標系中表示圓呢？由此引出課題，使學生都能夠跟上教師的節奏.接下來教師繼續提問：確定一個圓需要哪些條件？學生回答需要圓心和半徑.教師追問：在平面直接坐標系上，圓心坐標化相對容易，但是半徑坐標化怎么實現呢？經過教師的啟發和點撥，學生很快就知道平面內到定點的距離等于定長的點的軌跡稱為圓.最后教師給出圓與方程的簡易思維導圖（如下圖）.

在師生互動過程中，學生也會出現一些疑問，教師要給學生留出提問和質疑的時間，這樣才能夠確保消除全部疑難問題，使學生掌握本節課的精髓.這時有的學生提問：通過圓心和半徑能夠確定圓的標準方程，那么反過來，當知道圓的標準方程時，能否確定圓心和半徑呢？有的學生提問：求圓的標準方程還有哪些方法呢？還有的學生提問：如何利用方程判斷點在圓內和圓外的情況呢？教師及時為學生解答疑問，使數學課堂變成知識傳遞和交互的場所，師生之間充滿了默契，讓學生對數學學習不再畏懼，增強學生數學應用能力.而且教師還要對學生提出的問題進行匯總和整理，找到存在的共性問題，將其作為課堂講解的重點，引導學生積極探索數學未知領域，提高課堂教學質量.

2.2 借助人工智能，讓學生樂問

以前，教師設計的問題都是從教材中能夠直接找到答案的，對于學生的啟發效果并不好，使數學課堂變得枯燥，學生不愿意配合數學教師.在新的教育環境下，數學教師能夠認識到數學問題的重要性，逐步轉變固有的教學思維，引入人工智能等新型教學手段，使數學課堂煥發生機，將繁瑣的數學知識簡單化，打開學生的思維.尤其是一些立體性和抽象性較強的數學知識，通過信息技術就可以直觀、形象地呈現出來，改變了學生對數學的錯誤認識，使他們樂于參與互動、樂于進行提問，掌握更多的數學思想方法.

微課的應用得到了廣大師生的青睞，有效解決了數學重難點，讓學生隨時隨地進行學習，展現出數學知識的魅力.比如講高中數學圓的標準方程，要想讓學生重視本節課的內容，教師要學會合理分析學情，根據學生的不同特點，設計不同難度的微課視頻，從多個層面去培養學生用坐標法研究幾何問題的興趣，深化數形結合思想.圓是最簡單的曲線之一，是學習三大圓錐曲線的基礎，為曲線和方程的理論教學作好準備.數學教師可以通過多媒體展示數學知識，一方面讓學生心中有數，知道數學知識是環環相扣的，另一方面也提高學生推理和分析的能力，在動手和動腦中獲得成長的動力.運用問題鏈，使學生的探究活動貫穿課堂的始終，從推導圓的標準方程到應用圓的標準方程，使學生的有效思維量加大.在數學課堂上，教師借助人工智能為不同層次的學生設計了多元題庫，當大屏幕上的教學系統抽取到學生時，會自動為學生匹配相應難度的數學問題，這樣就避免了“一刀切”的現象，使探究氣氛達到高潮.另外，虛擬技術的運用也給數學課堂增添了新鮮血液，讓學習數學如同做游戲一樣有趣.學生在自己的電子白板上進行操作，從形的角度入手，繪制圓心、半徑等，出現疑問可以通過線上的方式提出，實現一對一的輔導，為學生制定個性化的學習方案.當學生對基礎知識有了一定的掌握后，還可以完成電子白板中的“能力訓練”模塊，從不同的題型中訓練邏輯思維，使學生解決問題的思路更趨向于理智.

2.3 強化問題意識，讓學生會問

與初中數學相比，高中數學的知識體系更為復雜，需要學生具備較強的問題意識，能夠從學習過程中發現問題、解決問題，總結出學習數學的一般方法.在實際教學中，數學教師應該合理選擇提問時機，在學生感到疑惑處、在學生注意力不集中處、在考試易考點處設計問題，引導學生主動擴展問題范圍，讓學生能夠適應課堂中出現的各種變化，使師生關系更加和諧.同時，數學教師要為學生提供提問的機會，通過設置不同類型的“陷阱”，鍛煉學生的提問能力，讓學生每次都能提問到點子上，從而尋找到合理的突破口，強化自信心和自尊心.

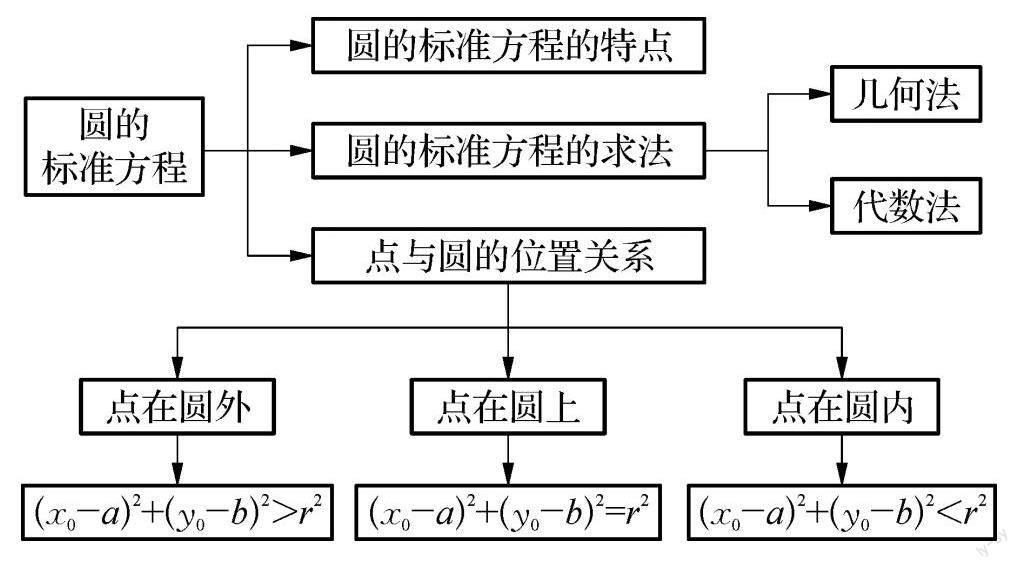
鍛煉學生問題意識的方式有很多，需要教師靈活選擇，因材施教，使學生形成閉環的思維系統，運用數學知識武裝自己的頭腦，把課堂還給學生.首先學生必須要有收集問題的思維，無論是在學習中還是生活中都會有很多數學問題，需要學生運用敏銳的洞察力去挖掘，建立對數學學科的熱愛.其次學生要有篩選問題的思維，當面臨著形形色色的問題時，需要取其精華，去其糟粕，準確把握數學知識之間的關系，促進知識遷移.最后學生還要有解決問題的思維，通過親身實踐去尋找靈感，更加專注于解題，能夠做到有的放矢.在教學“圓的標準方程”時，數學教師精心制作了本節課的框架圖，要求學生按照框架圖去填充知識，在這個過程中學生會產生一些問題，恰好成為師生交流的抓手，使學生有機會去提問.

在教學時，教師可以鼓勵學生繪制出個性化的框架圖，展現學生的聰明才智.對于優質的框架圖，教師要給予表揚，同時將其上傳到校園網中，為其他學生樹立榜樣，發揮先進帶后進的作用.問題意識是學生學好數學的關鍵所在，經過不斷的訓練，學生提出的問題都非常具有代表性和典型性，認知結構和心理特征逐步完善，也有利于培養學生的探索求知的精神.有的學生向教師提問：將圓的標準方程展開后會是什么形式？教師可以將這個問題作為學生探究的對象，還可以利用互聯網查找其他學生的操作，從而進行數學的再發現、再創造.

2.4 拓展實踐活動，讓學生善問

獲取數學知識的途徑是多方面的，不能完全局限于課堂上，數學教師要帶領學生參與各類實踐活動，拓展學生的知識面，給學生施展才華的機會，讓學生在實踐中進行提問和質疑，激發創新思維.教師在教學時要講究循循善誘， 鼓勵學生進行探究式學習，對于一些數學問題不設置固定的答案，讓學生在探究中自悟.數學實踐活動是學科育人的重要途徑，學生能夠在實踐中體會“形”與“數”的轉換，改變學生學習數學的生態.

通過對近幾年的高考試題分析，發現在高考數學試卷中經常會出現一些關于圓的題目，但是并沒有直接給出圓的信息，而是將其隱藏在生產、生活的案例中，需要經過分析和轉換才能夠進一步的解題.數學教師為學生帶來生活中關于圓的實際問題，創設良好的實踐情境，注重啟發與探究雙管齊下，讓學生感受到數學文化.如一個可以雙向行駛的隧道，它的截面是半圓形，隧道的半徑是4米，假設一輛貨車駛入隧道，貨車寬3米，高2.7米，問這個貨車能通過隧道嗎？當學生剛拿到問題的時候可能會感覺到有些棘手，但是只要將所學的知識聯系起來，問題就會迎刃而解.在解這個題的時候，學生不僅要具備圓的知識，還要知道汽車在公路上行駛是不能跨越中心線的.教師指導學生利用圓的對稱性來創建直角坐標系，學生很快就能夠求出半圓的標準方程，最終得到貨車的高度，要高于隧道的高度，所以貨車不能夠通過隧道.此時學生可能會產生疑問：那么將這個貨車的高度降到多少時才能夠通過隧道呢？這個提問是非常有價值的，應該得到教師的重視，因為它將圓的標準方程與最值問題進行了結合，順利將數學課堂推向了高潮.“學貴有疑，有疑才有思”，數學教師還要組織學生進行項目式的實踐活動，將學生分成學習小組，發揮集體的優勢，對數學問題的探究更透徹，激發學生思維潛能.

3 結 語

總之，利用問題引導學生探究，激發其求知欲望，促進其能力發展，是教育改革的初衷，也是教師教學的目標.隨著核心素養理念的深入，高中數學教師必須要堅定教學理念，設計多樣性和層次性的數學問題，培養學生的問題意識，使他們的數學思維真正活躍起來，激發潛在的學習動機.還要善于抓住學生的興趣點，創造問題情境，指導學生釋疑、解疑，發展創新能力，實現以學定教的目標.

參考文獻：

［1］ 何蓮靈.高中數學“問題導學”式教學中如何引導學生有效解答［J］.中學課程輔導，2019（17）：25 26.

［2］ 吳莉莉.將問題作為驅動高中數學探究的助力器［J］.數學學習與研究，2022（11）：41 43.

［3］ 展江平.淺談問題探索法在高中數學教學中的運用［J］.中學課程資源，2014（1）：32 33.

［4］ 盛茜.問題導向下的高中數學探究式教學范式研究——以“圓的標準方程”的教學為例［J］.數學學習與研究，2022（8）：11 13.