關注問題設計，引導素養提升

陳超

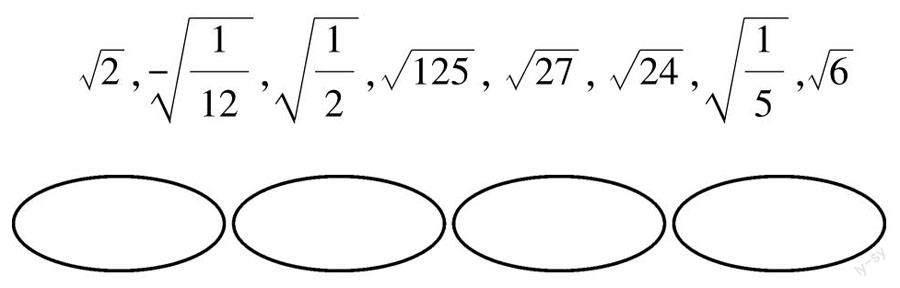
摘 要：《義務教育數學課程標準（2022年版）》指出，對于數與式的教學，教師應把握數與式的整體性.在二次根式的加減（1）的教學中筆者以關注數式通性、關注整體教學、關注素養培養為抓手進行教學設計.本文通過導入新知、建構新知、鞏固新知、深化新知、回味新知、延伸新知六個環節開展教學，從而有序培養學生的核心素養.

關鍵詞：課程標準；數式通性；單元視角；二次根式；核心素養

《義務教育課程標準（2022年版）》指出，對于數與式的教學，教師應把握數與式的整體性^［1］.因此，對于二次根式的加減運算，在教學中筆者主要以關注數式通性、關注整體教學、關注素養培養為抓手進行教學設計.所謂關注數式通性，就是引導學生在回顧前面學習的同類項的概念、合并同類項法則及整式加減的步驟的基礎上，構建同類二次根式的概念、二次根式加減的法則以及二次根式加減的步驟；所謂關注整體教學，就是在整個單元視角下設計教學任務，同時讓學生及時有效地類比前面學過的有理數、實數、整式、分式的相關知識點，并完成對應的生長性的思維導圖；而素養培養，則是在具體的教學活動中，凸顯“四基”和“四能”，關注綜合實踐，從而有序培養學生的核心素養.2023年10月，筆者有幸參加了蘇州高新區教研室組織的教研活動，開設公開課一節，課題為“二次根式的加減（1）”，現將在磨課過程中的一些思考和教學過程以及反思整理如下：

1?教學分析

1.1?教材分析

“二次根式的加減”是蘇科版八年級下冊第12章第3節的內容，本節課是在學生已經學習了二次根式的定義、性質、化簡和乘除法運算等相關知識和有了相關研究經驗的基礎上展開的.同時，二次根式的加減與之前學過的實數的加減、整式的加減、分式的加減又有著密切的聯系，通過類比展開對二次根式的加減相關知識的研究能加深學生對數和式加減運算的研究方法的認識，也能為學生以后繼續研究數和式加減運算奠定基礎并且提供范式.在知識形成過程中，蘊含了類比、從特殊到一般、從具體到抽象等數學思想方法，對發展學生的運算能力、數據觀念、應用意識等核心素養有積極的作用.

1.2?學情分析

（1） 從學生知識基礎來看：學生已經學習了二次根式的定義、性質、化簡和乘除法運算等相關知識，這套學習數與式的范式對學生學習二次根式的加減有良好的引導作用.

（2） 從學生數學活動經驗來看：在之前“實數的加減”“整式的加減”和“分式的加減”的學習中，學生已初步了解了研究的路徑，具備了一定的獨立思考和歸納總結等能力.

1.3?視角分析

在大單元教學的視角背景下，引導學生歸納所學數與式知識點的結構框架、類比總結出研究數與式的一般路徑：定義→性質→運算→應用，顯得很有必要.為此，我打算在學生合作討論的基礎上，引導學生歸納所學數與式知識點的思維導圖，從而體現數學知識點在課堂上的有效生成，真正做到以學生為主體，充分發揮學生的主觀能動性，從而實現新課標要求的“整體把握教學內容，注重教學內容的結構化”，真正落實核心素養的提升.

2?教學設計

2.1?創設情境，導入新知

同學們，在剛剛結束的第19屆杭州亞運會上，我國體育健兒不畏困難，不懼挑戰，取得了201枚金牌、111枚銀牌、71枚銅牌，共383枚獎牌的好成績.小明同學想在亞運會手抄報上規劃出三個區域畫亞運會的吉祥物，如圖所示.如果這三塊區域設置成正方形.

（1）若從左往右的3個正方形的面積分別是4、16、9，求線段AD的長度.

（2） 若從左往右的3個正方形的面積分別是4a²、16a²、9a²（a＞0），求線段AD的長度.

你能說說這是什么運算嗎？你是如何運算的呢？

設計意圖：通過介紹生活中的實際問題，激發學生的學習興趣.引導學生回顧前面學習的實數的加減法運算和整式的加減法運算.

（3） 若從左往右的3個正方形的面積分別是2、18、8或3、27、12或5、45、20.

你能分別列出求線段AD長的算式嗎？

追問1：你能說說這是什么運算嗎？

追問2：你能說說上面算式中的3組二次根式各有什么共同特征嗎？

追問3：你能給具有這些特征的二次根式取一個合適的名字嗎？

追問4：為什么取這個名字呢？

追問5：你能給同類二次根式下個定義嗎？

設計意圖：通過設置一系列追問，在對實數的加減法和整式的加減法回顧的基礎上，引入二次根式的加減法的學習.同時，利用問題串引導學生類比前面學習的“同類項”的概念，并自主歸納總結出“同類二次根式”的概念.

2.2?類比學習，建構新知

經過化簡以后，被開方數相同的二次根式，叫做同類二次根式.

找一找：請找出同類二次根式，并整理在框圖內.

設計意圖：通過設計“找一找”的數學活動，讓學生進一步理解和應用“同類二次根式”的定義.通過對被開方數為分數的二次根式的化簡，鞏固前面學習的最簡二次根式，從而為學生本節課的進一步學習打下基礎.

2.3?數學運用，鞏固新知

設計意圖：以計算題“意外情況的出現”為素材，進一步提升學生發現問題、提出問題、分析問題和解決問題的能力.同時，引導學生發現類比的負遷移現象.通過“平方法”和“作差法”的滲透，進一步提升學生的運算能力和推理能力等.

例2?兩個圓的圓心相同，半徑分別為Rcm、rcm，面積分別是18πcm²、8πcm².求圓環的寬度（兩圓半徑之差）.

變式：兩個圓的圓心相同，半徑分別為Rcm、rcm，面積分別是18cm²、8cm².求圓環的寬度（兩圓半徑之差）.

設計意圖：考慮到部分學生在計算被開方數是分數的二次根式時，經常算錯.通過設計題目的階梯，來分層引導學生計算生活中常見圓環圖形的寬度，為學生學習被開方數是分數或分式的二次根式的化簡，提供較好的范例，讓學生積累一定的經驗，從而提升學生的運算能力和應用意識，進一步感受數學和生活的緊密聯系.

2.4?聯系實際，深化新知

算一算：現有一塊長8dm、寬3dm的木板，采用如圖的方式，在這塊木板上能否截出3個面積分別是4.5dm²、8dm²、4.5dm²的正方形木板？

設計意圖：通過將問題情境中的三個正方形問題改編為生活中的截紙板問題，讓學生感受到數學來源于生活，又高于生活，最終服務于生活這一理念.通過讓學生自主探究“能否截出”，鍛煉學生發現問題、提出問題、分析問題、解決問題的能力，從而有序發展學生的運算能力、推理能力和應用意識等數學核心素養.

2.5?課堂小結，回味新知

設計意圖：給學生充足的時間來回顧第12章二次根式的學習過程，再引導學生對研究的路徑進行小結，并完成思維導圖.以回顧為契機，培養學生的總結能力，充分發揮學生的主體作用.讓學生感受到數與式等數學知識的生長過程，關聯數式通性，從而實現算法的順利遷移^[2].

2.6?分層作業，延伸新知

必做題： 書本163—164頁練習第1、2題.

選做題：整理已學的數與式的相關知識點，嘗試從知識內容、過程方法、運算法則等角度自主構建知識框架.

設計意圖：作業分必做題和選做題，讓不同層次的學生都得到相應的發展.通過學生課后的獨立思考、自主歸納進一步發展自身的數學核心素養.

3?教學反思

3.1?注重設問，培養能力

發現問題是研究數學問題的核心環節，那么在數學課堂教學中，老師通過一系列嚴謹縝密的設問，引導學生探索數學知識，就顯得尤為重要.好的設問可以激發學生的求知欲、讓教學目標落地生根并有序推進.相反，脫離實際的隨意提問，會讓學生一頭霧水，抓不住重點.本節課通過一系列的追問，引導學生類比歸納總結出同類二次根式的定義和二次根式加減的法則和步驟，體現了較好的教學效果.通過引導學生由數學學科內實數的加減到整式的加減再過渡到本節課二次根式的加減，讓學生感受數學知識的生長過程，也為學生在本節課學習結束時，總結、設計所學知識點的思維導圖做鋪墊.

3.2?類比遷移，發展素養

3.3?拓展延伸，回歸生活

為了呼應本節課開始研究的拼在一起的三個正方形的面積問題，設計出“算一算”環節，讓學生解決生活中的應用題.在學生充分討論的基礎上，小組合作探討能否截出的具體意義，即：拼在一起的三個正方形的最大寬度需要不大于3dm，拼在一起的三個正方形的總長度不大于8dm，從而解決實際問題.讓學生感受到數學來源于生活，又高于生活，最終服務于生活.同時，進一步發展學生的運算能力、推理能力、應用意識等核心素養.

參考文獻：

［1］ 中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.

［2］ 李樹平.關聯數式通性?提升數學素養：“二次根式的加減（1）”教學設計與教學實施反思［J］.中學數學月刊，2023（7）：47-50.

［3］ 姜夢潔，劉冰楠.情境化數學問題的設計研究：以“弧度制”教學設計為例［J］.高中數學教與學，2023（20）：54-57.

［4］ 秦哲.關注問題梯度，提升解題能力：以“一次函數面積問題”教學設計為例［J］.中學數學，2023（20）：21-22+27.

［5］ 孫鋆.素養導向下數學概念問題鏈教學再設計：以“平面”概念的教學設計為例［J］.中小學數學（高中版），2023（7）：74-76.

［6］ 吳康.混合型切比雪夫方程探索［J］.數學之友，2022，36（5）：64-65.

［7］ 魯和平.構造拋物線巧解向量題［J］.數學之友，2022，36（5）：69.

基金項目：江蘇省教育科學“十四五”規劃2021年度課題：“雙減”背景下初中數學作業優化設計的研究（課題編號：C-c/2021/02/78）.