SOLO分類理論視閾下的高考試題學業述評分析

摘? 要：應用SOLO分類理論，對2022年全國新高考Ⅰ卷的知識能力和學生思維水平結構進行分析，得出關于強化SOLO分類理論視閾下學業述評的內涵，深化SOLO分類理論視閾下學業述評的內核，促進學習深度發生和“教—學—評”一致性的啟示和教學建議.

關鍵詞：高考數學；SOLO分類理論；學業述評

《深化新時代教育評價改革總體方案》指出：探索建立中小學教師教學述評制度，任課教師每學期須對每位學生進行學業述評. 隨著新課程改革及教育評價制度的深入推進，重視定量認識、重視定性分析、關注核心素養的“學業述評”將成為教師評價學生的重要手段之一. 為了促進學生改進學習方法而進階學習，如何有效開展學業述評？這是當前亟須解決的實踐問題.

本文應用SOLO分類理論，對2022年全國新高考Ⅰ卷的知識能力和學生思維水平結構進行分析，以期對日常教學及其評價有所啟發.

一、基于SOLO分類理論視閾的學業述評基本內涵

1982年，澳大利亞教育學家彼格斯根據皮亞杰的認知發展階段論，創建了“SOLO分類理論”（Structure of the observed learning outcome），即可觀察的學習成果結構. 該理論是一種以等級描述為特征的質性評價研究方法. SOLO分類理論的基本理念，主要是針對學生回答某一問題展現出來的不同思維層級，將其思維能力水平按從簡單到復雜、從低到高的原則劃分為前結構水平（Prestructural，P）、單點結構水平（Unistructural，U）、多點結構水平（Multistructural，M）、關聯結構水平（Relational，R）、抽象擴展結構水平（Extended Abstract，Ea）. 據此，能較好地評價學生思維能力所達到的廣度和深度，體現對學生的學習從量變到質變的測量與評價.

SOLO分類理論視閾下的學業述評，是根據學生學習結果呈現的SOLO水平，運用SOLO分類理論，從學業基礎、主要問題、建議措施和進階路徑等維度，對不同學習水平的學生的學業進行具體敘述和質性評價，可因材、因地靈活施評，是促進學生進階學習和發展數學核心素養，以及檢驗教師課堂“教—學—評”一致性程度和教學質量的有效手段.

二、基于SOLO分類理論的2022年全國新高考Ⅰ卷試題分析

1. SOLO結構水平層次的劃分標準

分析發現，《中國高考評價體系》“四翼”考查要求與SOLO思維層次及水平特征在基本思想上一致，在邏輯上相匹配，如表1所示.

因此，本分析融合考查載體、知識獲取、實踐操作、思維認知等評價維度，將表1作為SOLO結構水平層次的劃分標準.

2. SOLO結構水平層次及水平特征試題分析范例

依據表1，以2022年全國新高考Ⅰ卷中的部分典型試題為例，對SOLO結構水平層次及水平特征進行解釋性的范例分析. 由于前結構水平描述的是學習者不能解答問題的狀態，故不進行范例分析.

（1）單點結構水平（U）.

例1 （第4題）南水北調工程緩解了北方一些地區水資源短缺問題，其中一部分水蓄入某水庫，已知該水庫水位為海拔148.5 m時，相應水面的面積為140 km2；水位為海拔157.5 m時，相應水面的面積為180 km2. 將該水庫在這兩個水位間的形狀看作一個棱臺，則該水庫水位從海拔148.5 m上升到157.5 m時，增加的水量約為（? ? ）.（[7]≈ 2.65）

（A）1.0 × 109 m3 （B）1.2 × 109? m3

（C）1.4 × 109? m3 （D）1.6 × 109? m3

【評析】此題以“南水北調工程”為簡單問題情境，主要考查棱臺的體積公式和學生的應用意識，屬基礎性問題. 學生可以運用棱臺體積公式單一知識點解決問題. 此題考查的學科知識內容及能力為單一知識結構. 因此，可以歸屬于SOLO結構水平層次中的單點結構水平，屬于低階思維等級.

（2）多點結構水平（M）.

例2 （第10題）已知函數[fx=x3-x+1，] 則（? ? ）.

（A）[fx]有兩個極值點

（B）[fx]有三個零點

（C）點[0，1]是曲線[y=fx]的對稱中心

（D）直線[y=2x]曲線[y=fx]的切線

【評析】此題主要考查三次函數的性質及導數的應用，考查學生的邏輯推理和數學運算素養，屬基礎性問題. 學生能運用試題選項中的多個孤立的知識點解決問題. 此題考查的學科知識內容和能力相對獨立、多元化. 因此，可以歸屬于SOLO結構水平層次中的多點結構水平，屬于中低階思維等級.

（3）關聯結構水平（R）.

例3 （第8題）已知正四棱錐的側棱長為[l，] 其各頂點都在同一球面上. 若該球的體積為[36π，] 且[3≤][l≤33，] 則該正四棱錐體積的取值范圍是（? ? ）.

（A）[18， 814] （B）[274， 814]

（C）[274， 643] （D）[18， 27]

【評析】此題主要考查四棱錐的體積公式和導數的應用，考查的能力素養涉及直觀想象、數學建模和邏輯推理等，屬于綜合性問題. 學生需要運用多個知識點，且進行有效整合，方可解決問題. 首先，要建立正四棱錐體積目標函數；其次，要結合目標函數的結構特征尋找問題解決方案，并有機整合導數知識，綜合分析、解決問題. 此題考查的學科知識內容和能力要求具有較強的關聯性. 因此，可以歸屬于SOLO結構水平層次中的關聯結構水平，屬于中階思維等級.

（4）抽象擴展結構水平（Ea）.

例4 （第7題）設[a=0.1e0.1，b=19，c=-ln0.9，] 則（? ? ）.

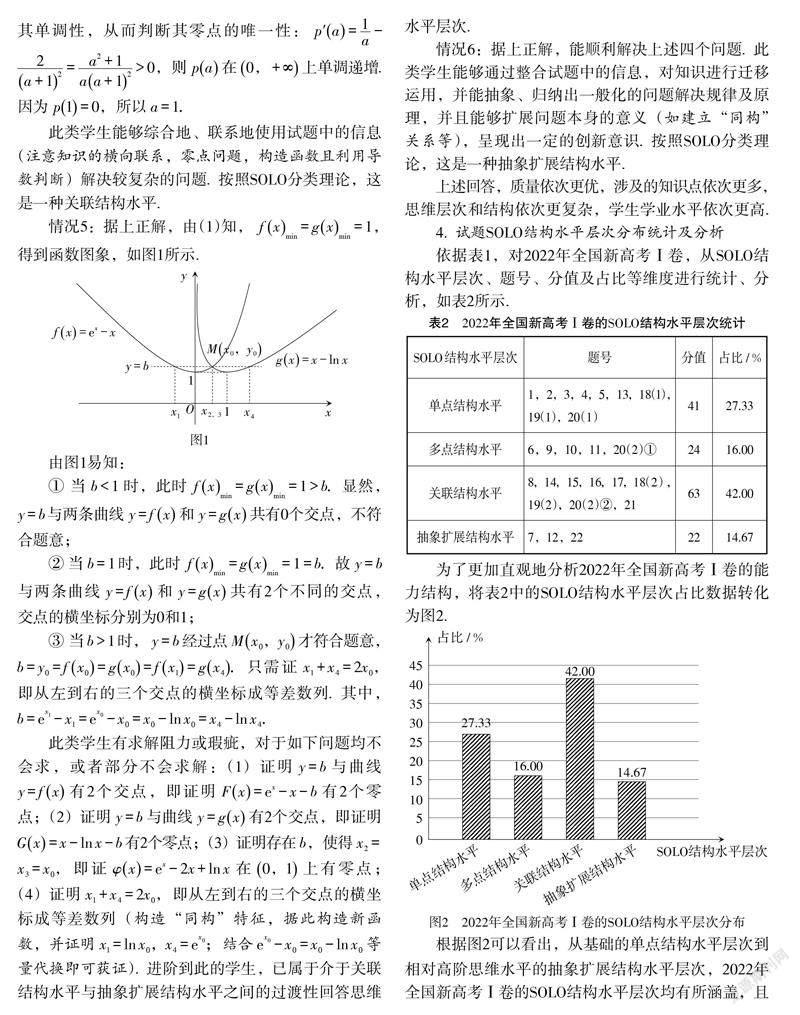
（A）[a

（C）[c

【評析】此題主要考查導數的應用. 需要構造函數，對學生的數學抽象能力、邏輯推理能力和綜合應用知識解決實際問題的能力有較高要求，屬于應用性、創新性問題. 解決該問題時，學生需要從陌生、具體的問題情境中，抽象出隱含的函數構造的信息，并把已有導數知識遷移、拓展到新情境中，進行探究性思考. 此題考查的學科知識內容和能力要求，需要學生具有較強的歸納、演繹、抽象、思維發散和創新能力. 因此，可以歸屬于SOLO結構水平層次中的較高抽象擴展結構水平，屬于高階思維等級.

3. 學生答題SOLO結構水平層次分析范例

例5 （第21題）已知函數[fx=ex-ax]和[gx=ax-][lnx]有相同的最小值．

（1）求[a;]

（2）證明：存在直線[y=b，] 其與兩條曲線[y=fx]和[y=gx]共有三個不同的交點，并且從左到右的三個交點的橫坐標成等差數列．

【評析】此題利用導數研究函數（含參數）的性質，主要考查函數與導數的相關內容知識：單調性、最值及零點問題等，涉及函數零點存在定理等知識；考查分類討論和轉化與化歸思想，考查邏輯推理和數學運算素養及創新意識，屬于應用性、創新性問題中的難題. 試題主要以復雜、探究性問題情境為載體，測量與評價學生主動思考、探究的意識，考查學生的“四能”和創新思維能力. 此題考查的學科知識內容和能力要求呈現抽象、遷移、歸納與演繹等思維操作. 因此，可以劃分為SOLO結構水平層次中的抽象擴展結構水平，屬于高階思維等級.

對于該問題，學生一般有以下6類典型答題情況.

情況1：完全不會，無法作答；或者求[fx=ex-][a，gx=a-1x]時，全部或部分出現錯誤.

此類學生存在的問題是知識儲備不足，不會利用導數求函數的單調性、最值等. 按照SOLO分類理論，這是一種前結構水平.

情況2：（1）求出[fx=ex-a，gx=a-1x，] 從而求得[fx]在[-∞，ln a]單調遞減，在[ln a，+∞]單調遞增；[gx]在[0， 1a]單調遞減，在[1a，+∞]單調遞增. 故[fxmin=fln a=a-aln a，gxmin=g1a=1-ln1a.]依題設有[a-alna=1-ln1a.]

此類學生關注問題中的有效信息“最小值相等”，并能夠回答問題，但快速收斂回答，忽視了解答過程中出現的“思維不嚴密”的矛盾，即需要分類討論、補充完善“當[a>0]時”和“當[a≤0]時（不合題意）”的情形，體現了學生對分類討論思想掌握不牢. 按照SOLO分類理論，這是一種單點結構水平.

情況3：據上正解，觀察[a-alna=1-ln1a，] 可得[a=1.] 學生快速收斂回答，但不知道如何判斷并證明該方程解的唯一性.

此類學生能夠使用試題中包含的幾個獨立的信息（對參數分類討論，并觀察方程特征，求其解）解決問題，但對問題的整體結構缺乏整合能力. 按照SOLO分類理論，這是一種多點結構水平.

情況4：據上正解，依題設有[a-alna=1-ln1a，] 即[lna-a-1a+1=0.] 令[pa=lna-a-1a+1，] 利用導數判斷其單調性，從而判斷其零點的唯一性：[p′a=1a-][2a+12=a2+1aa+12>0，] 則[pa]在[0，+∞]上單調遞增. 因為[p1=0，] 所以[a=1.]

此類學生能夠綜合地、聯系地使用試題中的信息（注意知識的橫向聯系，零點問題，構造函數且利用導數判斷）解決較復雜的問題. 按照SOLO分類理論，這是一種關聯結構水平.

情況5：據上正解，由（1）知，[fxmin=gxmin=1，] 得到函數圖象，如圖1所示.

由圖1易知：

① 當[b<1]時，此時[fxmin=gxmin=1>b.] 顯然，[y=b]與兩條曲線[y=fx]和[y=gx]共有0個交點，不符合題意；

② 當[b=1]時，此時[fxmin=gxmin=1=b.] 故[y=b]與兩條曲線[y=fx]和[y=gx]共有2個不同的交點，交點的橫坐標分別為0和1；

③ 當[b>1]時，[y=b]經過點[Mx0，y0]才符合題意，[b=y0=fx0=gx0=fx1=gx4.] 只需證[x1+x4=2x0，] 即從左到右的三個交點的橫坐標成等差數列. 其中，[b=ex1-x1=ex0-x0=x0-lnx0=x4-lnx4.]

此類學生有求解阻力或瑕疵，對于如下問題均不會求，或者部分不會求解：（1）證明[y=b]與曲線[y=fx]有2個交點，即證明[Fx=ex-x-b]有2個零點；（2）證明[y=b]與曲線[y=gx]有2個交點，即證明[Gx=x-lnx-b]有2個零點；（3）證明存在[b，] 使得[x2=][x3=x0，] 即證[φx=ex-2x+lnx]在[0，1]上有零點；（4）證明[x1+x4=2x0，] 即從左到右的三個交點的橫坐標成等差數列（構造“同構”特征，據此構造新函數，并證明[x1=lnx0，x4=ex0;] 結合[ex0-x0=x0-lnx0]等量代換即可獲證）. 進階到此的學生，已屬于介于關聯結構水平與抽象擴展結構水平之間的過渡性回答思維水平層次.

情況6：據上正解，能順利解決上述四個問題. 此類學生能夠通過整合試題中的信息，對知識進行遷移運用，并能抽象、歸納出一般化的問題解決規律及原理，并且能夠擴展問題本身的意義（如建立“同構”關系等），呈現出一定的創新意識. 按照SOLO分類理論，這是一種抽象擴展結構水平.

上述回答，質量依次更優，涉及的知識點依次更多，思維層次和結構依次更復雜，學生學業水平依次更高.

4. 試題SOLO結構水平層次分布統計及分析

依據表1，對2022年全國新高考Ⅰ卷，從SOLO結構水平層次、題號、分值及占比等維度進行統計、分析，如表2所示.

為了更加直觀地分析2022年全國新高考Ⅰ卷的能力結構，將表2中的SOLO結構水平層次占比數據轉化為圖2.

根據圖2可以看出，從基礎的單點結構水平層次到相對高階思維水平的抽象擴展結構水平層次，2022年全國新高考Ⅰ卷的SOLO結構水平層次均有所涵蓋，且分布梯度合理：① 以關聯結構水平（R）作為主要考查的能力結構水平，試題分值占全卷總分值的42.00%，凸顯了高考試題的綜合性，強調知識的結構化和聯系性；② 單點結構水平（U）和多點結構水平（M）層次試題，分值合計占全卷總分值的43.33%，凸顯了高考試題深化基礎性考查，強調關注學科主干知識、學生必備知識和“雙基”；③ 抽象擴展結構水平（Ea）試題，分值占全卷總分值的14.67%，體現了高考試題注重數學的本質與創造性思維，深入考查了學生的關鍵能力和核心素養，強調問題解決中的知識遷移應用能力和思維品質，凸顯試題的選拔功能.

綜上可知，2022年全國新高考Ⅰ卷關注新課標、新教材、新高考要求的一致性，落實高考“一核”“四層”“四翼”的考查要求，注重教考銜接及高考對教學改革的導向和推動作用.

5. 試題知識領域SOLO結構水平層次分布統計及分析

依據表1，對2022年全國新高考Ⅰ卷，按照《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱《標準》）課程設置的四大主要內容領域進行分類統計，如表3和表4所示.

根據表3，可以看出：宏觀上，2022年全國新高考Ⅰ卷重點考查函數和幾何代數主干領域知識，且其主干知識的SOLO結構水平層次以關聯結構水平和抽象擴展結構水平層次為主，反映出試題突出對學生核心知識及其綜合應用、解決問題的能力的考查.

根據表4，可以看出：微觀上，數列、一元函數導數及其應用、立體幾何初步、平面解析幾何著眼于學生的思維能力進行考查，其他知識領域相對著眼于基礎性考查. 在一元函數導數及其應用重點知識板塊，著眼于創新思維的考查.

三、SOLO分類理論視閾下的學業述評

基于高考試題SOLO結構水平層次分析及其教學導向，教師提煉并開展基于SOLO分類理論視閾下的學業述評. 任務指向四個方面，以促進學生進階學習.（1）確定SOLO層次. 首先，從知識儲備、思維操作、結果一致性和回答結構等維度，將學生學習結果劃分為5個SOLO結構水平層次；然后，依據學生個體學習結果，確定學生學業能力所處的層次水平.（2）解析學生問題. 根據學生所處水平層次，從“四基”“四能”等方面對無法進階高一級SOLO結構水平層次的學生進行歸因分析.（3）提出改進建議. 依據學生學習中的具體問題，給予明確具體、可操作的學習建議，同時在學生落實建議的過程中對其進行糾偏和跟蹤輔導，促使學生能夠有目的、有計劃地逐步解決學習障礙并進階學習.（4）明確進階路徑. 指導學生從當前自身所處的SOLO結構水平層次出發，循序漸進，明確措施和方法，進階更高層次SOLO結構水平，如表5所示（以例5為例進行說明）.

四、啟示

基于上述過程，可知SOLO分類理論視閾下的高考試卷分析、學業述評分析，以及“教—學—評”一致性分析，是一個有機的整體，可以相互促進. 由此，筆者提出以下幾點思考.

1. 加強、豐富學業述評的內涵

對照《標準》和新高考要求，統籌規劃教學的深度與廣度，可以強化學業述評的內涵. 由前可知，2022年全國新高考Ⅰ卷對學生能力水平層次的考查，有注重關聯結構水平（R）和抽象擴展結構水平（Ea）、突出單點結構水平（U）的傾向. 因此，教學、命題需要強化內容的深度與廣度，學業述評需要強化、合理控制關聯結構水平（R）、抽象擴展結構水平（Ea）和突出單點結構水平（U）層次試題的分布比例. 既要關注不同層次的學生，又要指導和促進教、學與考的一致性，發揮高考的評價導向作用.

2. 凸顯學業述評的內核

著眼關鍵能力和核心素養培養，教學注重數學本質與創造性思維，可凸顯學業述評的內核. 質性評價是學業述評的內核，學業述評要從“學了多少”轉向側重“學得多好”. 教學和命題，著眼于發展學生的學科素養和學科能力，注重知識結構化和橫縱聯系的問題解決. 教學述評、學業述評就可以縱向深入，更好地體現質性評價的內涵和巨大價值. 反之，學業述評可以更好服務于教學及試題的命制策略：合理融入基于問題解決的內容、合理創設問題情境，重視引導學生運用所學知識進行理解與辨析、分析與推測、歸納與論證，綜合解決問題等，可以進一步明晰學習的進階方向.

3. 嵌入述評任務，促進學習深度發生

提高SOLO理論素養和試題命制水平，落實嵌入式教學述評任務，可以促進學習深度發生. 提高SOLO理論素養，可以精準、科學地把握命題素材的評價功能和目的，提升命題和分析的能力. 根據SOLO理論可知：在單點結構的基礎上，多點結構層次試題可以考查學生概括與總結多個孤立知識點的能力，其主要作用是增加知識點的覆蓋面，考查主干知識；關聯結構層次試題主要考查學生解答過程前階段所得結果與后續各階段知識、推理之間的聯系，考查學生利用特定的情境素材解決數學問題的能力，可以凸顯新課程的理念，體現新高考試卷的能力和素養立意，有利于選拔基礎扎實、綜合能力強的拔尖人才；抽象擴展結構層次的試題，則會提高試卷難度，提升試卷的區分度，但此類試題數量較多時會導致學生答題時間緊張，且易降低學生學習的積極性. 因此，試卷在滿足一定區分度的基礎上，可以適當增加關聯結構層次試題，通過創設多樣的問題情境，考查學生抽象擴展結構思維能力和創新意識. 同時，在教學中切實落實SOLO分類理論視閾下的學業述評“四個任務指向”，可以有效促進深度學習的發生.

五、結束語

SOLO分類理論視閾下的學業述評側重于質性評價（標準參照評價），強調個性化的因材施評、一人一案，即關注學生是否完成了既定目標任務（量與質），關注學生當前存在的問題，同時關注改進措施和進階路徑. 在平時的教學過程中，教師秉承“三位一體”（情境創設、活動組織、問題解決）的整體設計原則，開展嵌入式SOLO分類理論視閾下的學業述評活動，可以充分發揮教育評價的檢驗、診斷、反饋和激勵作用，有效促進“教—學—評”的一致性.

參考文獻：

［1］劉綠芹. SOLO分類理論視閾下的學業述評路徑探索［J］. 基礎教育課程（上），2022（4）：63-71.

［2］教育部考試中心. 中國高考評價體系［M］. 北京：人民教育出版社，2019.

［3］教育部考試中心. 中國高考評價體系說明［M］. 北京：人民教育出版社，2019.

［4］彼格斯，科利斯. 學習質量評價：SOLO分類理論可觀察的學習成果結構［M］. 高凌飚，張洪巖，譯. 北京：人民教育出版社，2010.

［5］劉斌，王濤耕，石一堅，等. 基于SOLO分類評價理論的高考地理試題的解構與分析研究：以2015—2019年全國新課標地理試卷Ⅱ卷分析為例［J］. 地理教學，2019（19）：53-57.

［6］王亞婷，周瑩. 新課標背景下高考數學試題SOLO思維層次研究：以 2019年高考數學全國卷為例［J］. 教育測量與評價，2020（4）：17-24.

作者簡介：吳光潮（1979— ），男，中學高級教師，主要從事中學數學教育教學研究.