變中有定，“揪”其根本
——以一道高三解析幾何調研題為例

江蘇省錫山高級中學 (214174)

陳 敏

一、引言

一題多解和多題一解是數學解題教學常用的教學方法.數學解題方法一般分為通法與巧法,通法著眼基礎，巧法著眼提高.通法是巧法的基礎，巧法是通法的升華.在目前的數學解題教學中，一方面，一些教師對通法推崇有加，而對巧法敬而遠之，甚至談“巧”色變，學生習慣于套用解題的固有套路與程式，思維僵化而無創新色彩，“韌”性有余而“靈”性不足；而另一方面，一些教師片面追求巧法，輕視基礎，缺乏對基本思想方法的挖掘與訓練，有時甚至陷入對通法不屑一顧而巧法又一時想不起的尷尬境界[1].當然，既要注重基礎，守住通法，又適時適度個性創新，催生巧法，“通”“巧”結合，“韌”“靈”并舉，這是我們解題教學的理想境界.但是這種魚和熊掌兼得的教學如何把握談何容易.筆者認為，無論通法還是巧法，變中還是有定的東西，仔細分析題意、提高目標意識、充分利用條件、尋找解題思路、綜合靈活選擇方法、解題后的總結與反思等等這些都是變中不變的的東西.在新情境下，選擇恰當的數學思想方法解決新問題的必備品格和關鍵能力，這才是根本之本.解析幾何問題一般通法與巧法變化比較多、運算量大，解題要求高，但是分析問題、解決問題的基本方向和基本思路是變中之定，數學解題就像數學本身一樣，應當是自然的、清楚的、明白的.本文從一道高三解析幾何調研題說起.

二、問題呈現

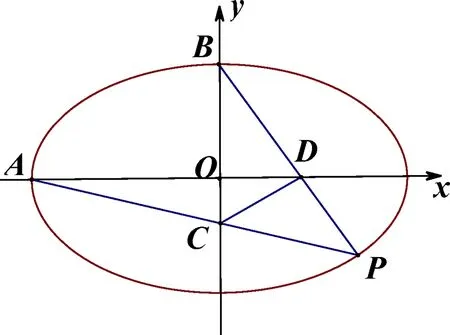
圖1

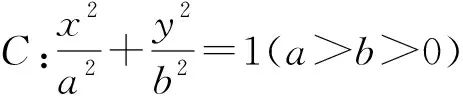
三、思路分析

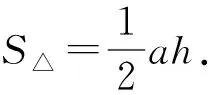
四、解題研究

(一)設線法

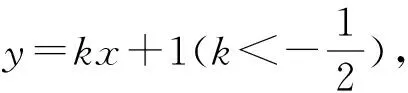
解題反思：反觀整個解題過程，目標很清晰，點P在第四象限、A，C，P三點共線等隱含條件條件的運用很充分，方法選擇也較為恰當.其中關鍵是利用割補的思想，把△PCD面積可以表示為△PBC與△DBC面積之差，以直線BP的斜率k為參數建立面積目標函數(也可以以直線AP的斜率為參數)，通過換元，利用基本不等式求出面積的最大值，解題過程中要注意k的范圍以及換元基本不等式中等號成立的條件，否則，可以用函數的單調性來解決.

設線法是解析幾何的通性通法，把直線方程與圓錐曲線方程聯立，得到一元二次方程，在判別式△>0的前提下，應用韋達定理、中點坐標公式、弦長公式等設而不求的方法解決相關問題.這種方法趨于定式，易于理解、掌握和運用，但這種方法往往運算量大，在考試的環境下，學生常常欲進維艱，耗時費力.

(二)設點法

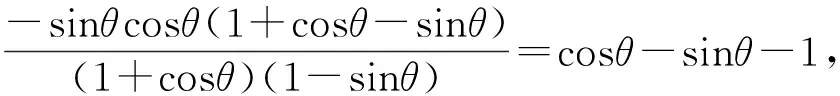
(三)動中有定

(四)變式研究

圖2

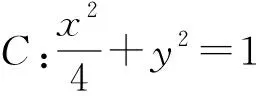
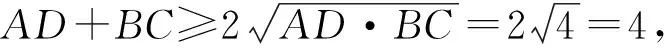
(五)轉換他求

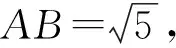
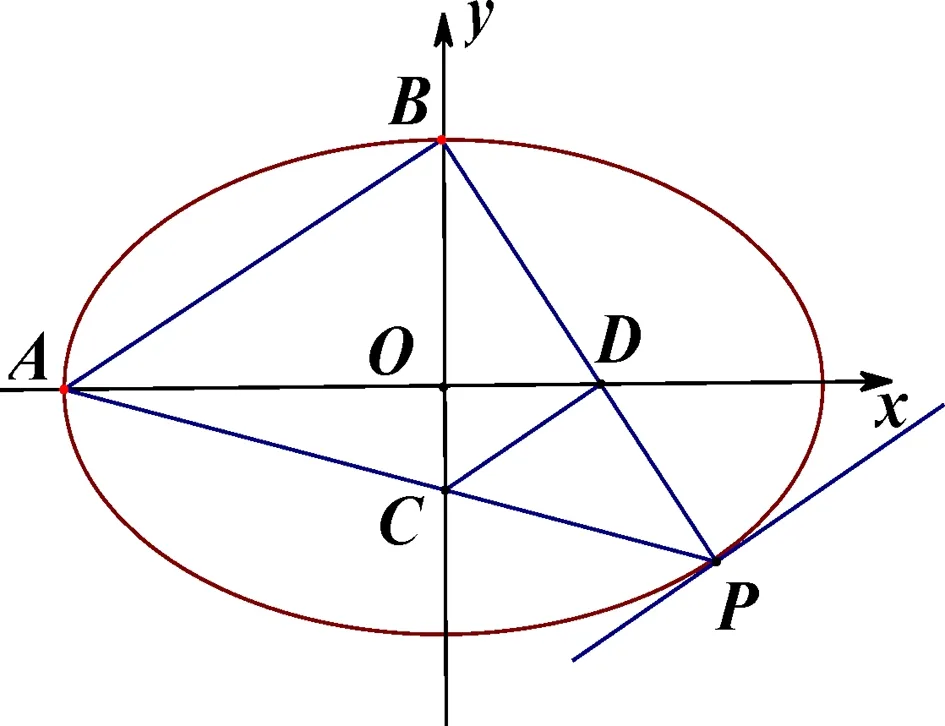
圖3

2.判別式法：如圖3，當與直線AB平行的直線與橢圓在第四象限相切時，點P到直線AB的距離的最大，此時點P就是切點.

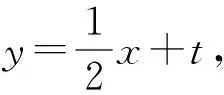
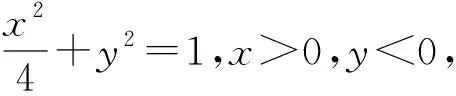
(六)回歸課本

圖4

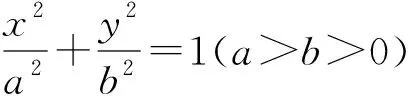
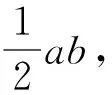
五、結語

以上對這道解析幾何調研題的解析，我們主要用了基本不等式法、換元法、參數法、判別式法、數形結合法、線性規劃法、導數法等思想方法，其中基本不等式法、換元法、參數法、判別式法屬于代數法，數形結合法、線性規劃法、導數法屬于幾何法，這些思想方法幾乎涵蓋了解析幾何常用的思想方法.如何靈活選擇恰當的數學思想方法，在新情境下解決新問題，這才是重要的，也是數學核心素養的根本要求.變中有定，“揪”其根本是實現這一根本要求的一條有效路徑.這里變中之定，根本之本，一方面是指仔細分析題意、提高目標意識、充分利用條件、尋找解題思路、綜合靈活選擇方法、解題后的總結與反思等等這些都是多變解法中不變的的東西；另一方面是指課本，課堂教學應“以課本為本”.學好教材是高考取得好成績的前提.我們要理解教材，“創造性使用教材”，而這樣做的第一要義是理解數學：了解數學概念的背景，把握概念的邏輯意義，理解內容所反映的思想方法，挖掘知識所蘊含的科學方法、理性思維過程和價值觀資源，學生養成良好的學習習慣，樹立敢于質疑、善于思考、嚴謹求實的科學精神；認識數學的科學價值、應用價值、文化價值和審美價值.