合理變形方程 巧妙計算斜率
——一道2022年高考題的另解與推廣

廣東省深圳市深圳科學高中 (518129)

馮廣軍 郭琳芳

2022年全國新高考Ⅰ卷第21題以雙曲線為載體，以圓錐曲線中定向問題與相關斜率之間的關系及三角形面積計算為切入點，考察了學生的數學運算，直觀想象和邏輯推理等核心素養.對于第一問，我們一般都是聯立直線與雙曲線方程來處理，但其實可以不必如此，因為橢圓、雙曲線方程中已經包含有兩種斜率形式，我們稍加變形便可以巧妙運用.

一、橢圓、雙曲線中斜率的兩種表達形式

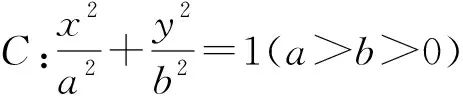
上述公式的證明非常簡單，只需要將兩點分別代入相應方程，然后做差即可.它已經利用到了橢圓或雙曲線的方程和直線與曲線的交點，因而應用時無需再聯立直線與橢圓或雙曲線方程，非常實用，下面以兩個高考題為例來看看這個公式的應用及推廣.

二、公式的應用

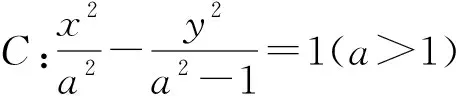
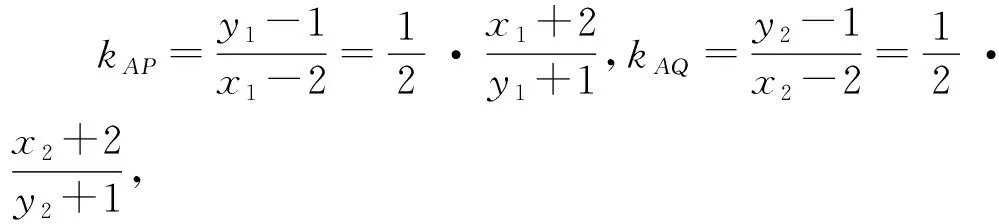
事實上，根據對稱性，由①到②時，我們只需要將x1換成x2，y1換成y2即可，借此，我們可以比較快速的將上述問題一般化.

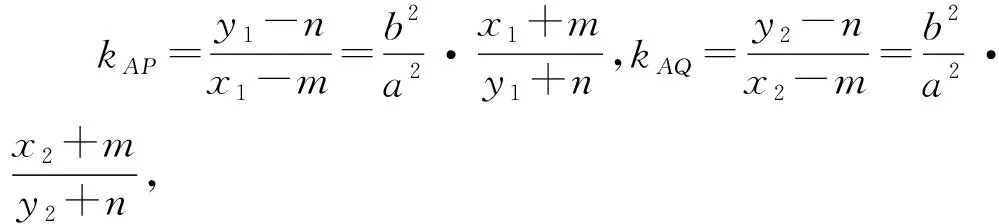
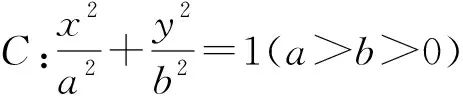
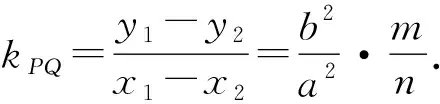
上述拓展都指向同一類型，定向問題，即直線的斜率為定值，若直線AP,AQ的斜率之和為非0常數λ，則此時直線l過定點，我們也很方便利用公式1或公式2求出相應定點，

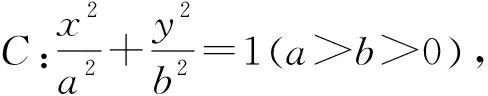
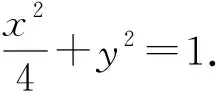
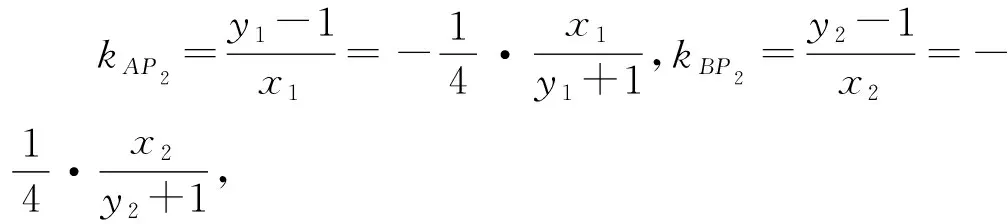
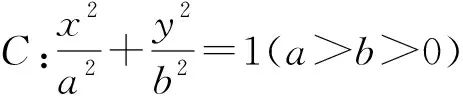
上述拓展皆可用公式1或公式2解決，此處省略推導過程.

三、反思與感悟

人教A版(2019版)教材第108頁例3和第121頁“探究”分別給出了橢圓和雙曲線的一種形成方式，這就提示我們：橢圓和雙曲線的軌跡既然可以用兩直線的斜率給出，那它們方程本身也應該包含有斜率表達式，事實上，我們只需要將坐標軸上的兩點換成關于坐標原點對稱的任意兩點即可，總之，教材蘊含無限寶藏，需要我們細細品味，慢慢開發.