三道全國高考數學試題的再思考

蘇州大學附屬中學 (215000)

許家釗

近日有幸學習了《中學數學研究》的三篇文章[1]，[2]，[3]，受益匪淺，也產生了一些自己的想法，現與讀者分享.

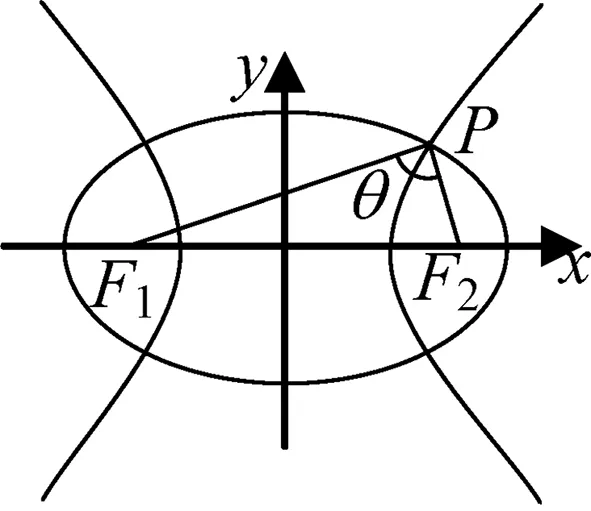
圖1

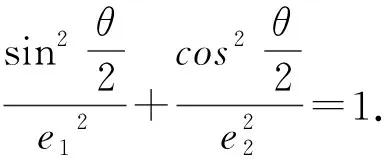
此方法要求學生熟悉焦點三角形面積公式，并對接下來的化簡要求較高.能否回歸橢圓和雙曲線的本源，回歸定義，使用學生熟知的通法加以證明？答案是可以的.證明如下：

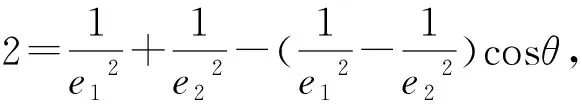
評析：焦點三角形面積公式也是采用圓錐曲線的定義、余弦定理以及三角變換知識得出的，筆者直接使用橢圓和雙曲線的定義，將焦點三角形△F1PF2三邊長都用離心率所需要的a和c來表示，再通過余弦定理便可以輕松證明，此方法邏輯鏈較為簡潔，便于此類問題的一般化處理，便于學生理解和掌握.

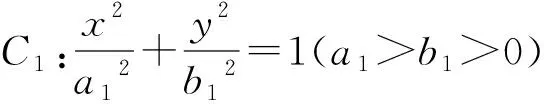
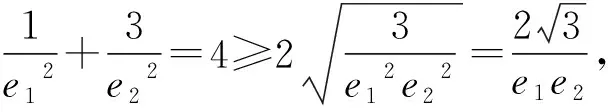
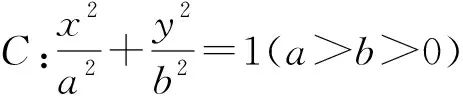
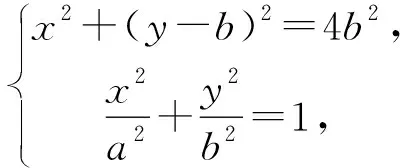
此方法前半段從幾何角度將試題轉化為圓與橢圓的公共點問題，角度新穎，運算量小，接下來分析臨界狀態，再根據離心率大小對橢圓形狀的影響，得出結論，這一步缺乏嚴謹性，對學生的分析和理解力要求較高.筆者給出如下證明.

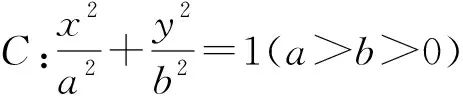
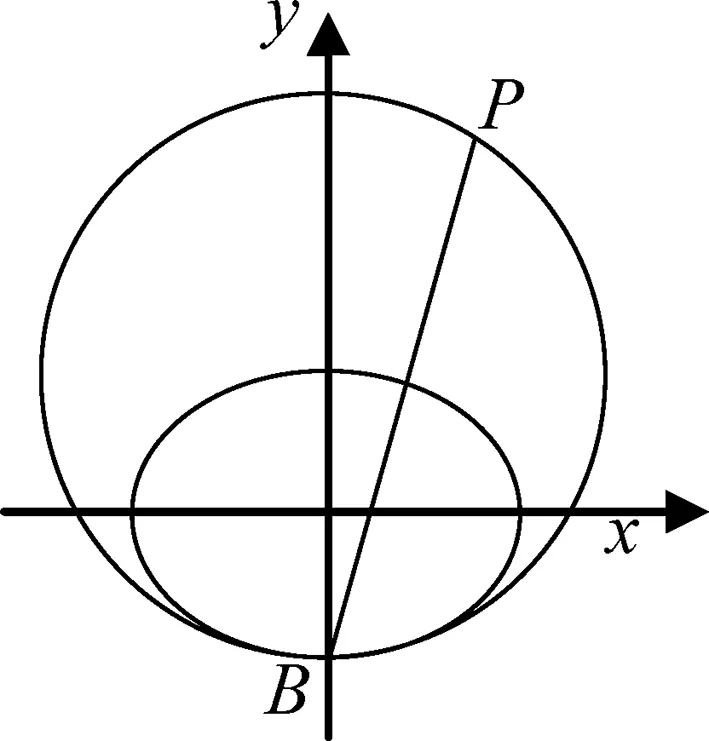
圖2

圖3

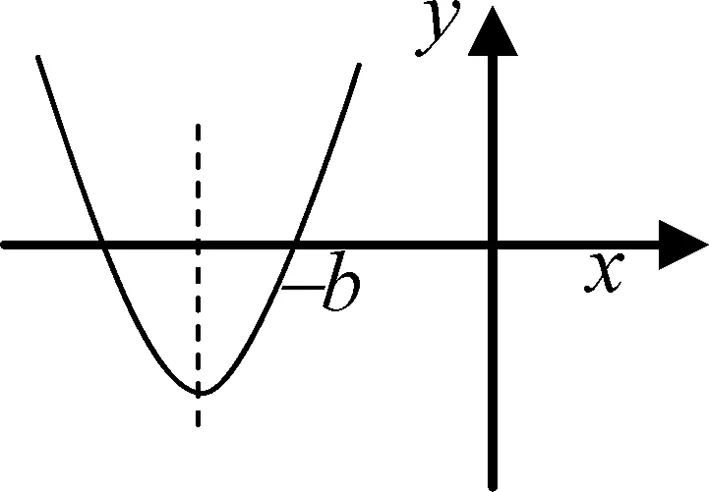
圖4

從幾何角度，采用數形結合的方法，得出試題的等價條件，避免了分析臨界狀態所帶來的不嚴謹性，提升了數學素養和思維能力，不得不說，這一道高考題命的是相當精彩，給老師和考生提供了很多的思考角度和空間.

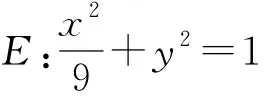
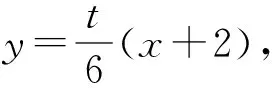
以上思路都算是常規思路，也便于理解，其中方法四最適合學生.但是，筆者覺得這些證明方法不足以揭示此類問題的實質，難以達到做一題通一類的效果.為此筆者給出如下證法.

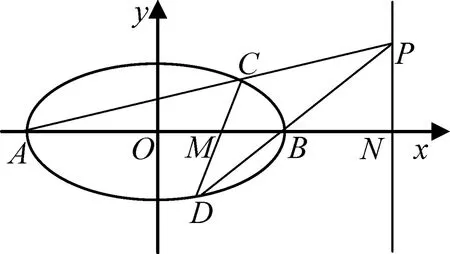
圖5

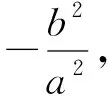
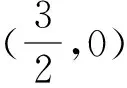
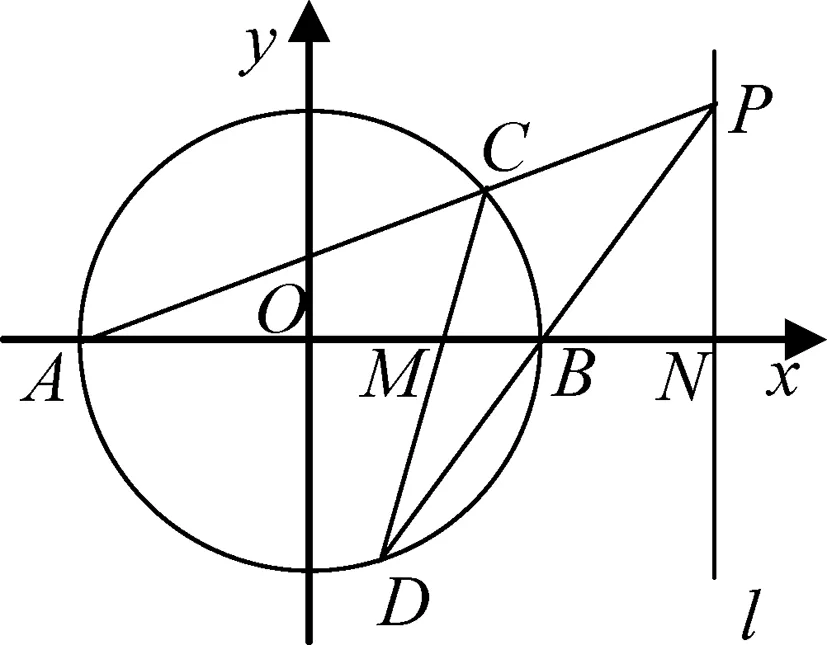
圖6

揭示實質：不妨通過仿射變換，將橢圓縱向均勻拉伸變換成圓，于是本題便成了這樣的問題：如圖6，圓O：x2+y2=a2中，直線l垂直于x軸，A(-a，0)，直線CD交于M，經過直線l上一點P連接AP，BP分別交橢圓于C，D，直線CD交x軸于M，則OM·ON=a2.

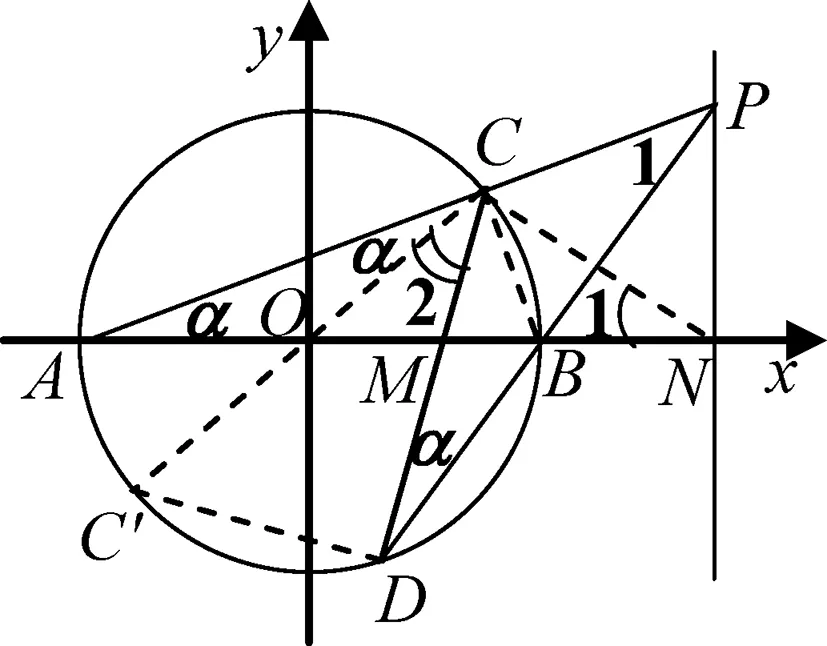
圖7

證明：如圖7，要證明OM·ON=r2，即證△OCM∽△ONC，即證∠OCM=∠ONC，即證圖中的∠1=∠2，因為∠BCP=∠BNP=90°，所以B、C、P、N四點共圓，所以∠BPC=∠BNC，記作∠1.又∠BDC=∠BAC=∠ACC′，記作α，△PCD中，∠1+α+∠DCP=180°，而∠2+α+∠DCP=180°，所以∠1=∠2，得證！

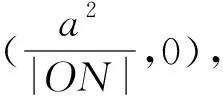
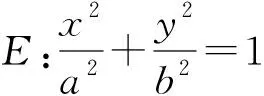
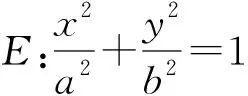
解決解析幾何問題的關鍵在于如何確定算理，優化算法，日常教學中，教師可以引導學生多角度思考問題，體會一題多解、多題一解.真正領會試題滲透的數學思想方法，領悟數學本質.