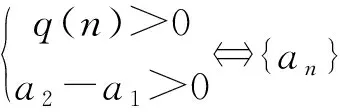遞推數列的單調性探究
浙江省衢州第二中學 (324000)
萬 祺
數列的單調性與有界性是數列的兩個基本性質,在解決具體問題時,兩者又相互關聯.本文主要探究一類已知遞推關系的數列單調性問題的解法,試圖總結并梳理一般處理此類問題的方法.
1.知識鋪墊
設數列{an},若對任意n∈N*,有an+1>an(an+1 為能更好地解決數列的單調性相關問題,我們引進一個定理: 下面用數學歸納法證明0 1°、n=1時,0 綜合1°、2°可知,對任意n∈N*,有0 說明:用做差方法判斷an+1-an的符號,一般地需要先證數列{an}的有界性,這也是判斷數列單調性最為常見的解法之一.另外,此題也可用數學歸納法證明0 1°、n=1時,0 分析:本題指的單調遞減包含了不嚴格單調減的情形,先直接作差尋找單調遞減的充要條件,再結合同號原則證明an所需要滿足的不等關系. 圖1 說明:方法一思路簡潔,目標明確,利用數列的單調有界定理,取n趨于無窮的情況進行必要性探路,這也為后續證明提供了理論基礎;方法二則是數形結合,利用蛛網圖及函數圖象的性質,在x軸上逐一標出xn,判斷單調性. 例5 (2017年浙江高考壓軸題節選)設x1=1,xn=xn+1+ln(1+xn+1),求證:0 提示:先用歸納法證明有界性xn>0,再由ln(1+xn+1)>0可知0 綜合上述分析,已知遞推關系an+1=f(an)的數列單調性問題的解決方案有: (1)直接作差判斷an+1-an=f(an)-an=g(an)的符號,即先求數列{an}的上下界,再結合函數y=g(x)的性質判斷符號; (3)數學歸納法證明an+1>an或an+1 (4)數形結合——畫出函數y=f(x)的圖象及函數y=x圖象,在x軸上逐一標出an(n=1,2,3,…),比較an與an+1大小,結合圖象判斷單調性. 另外,如果能通過遞推關系直接求出數列的通項公式an=f(n),也可直接判斷函數f(n)的單調性,進而說明數列{an}的單調性.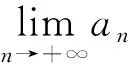
2.典例探究
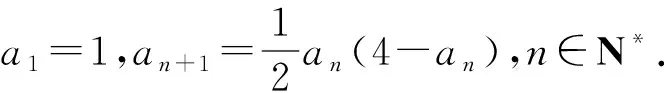
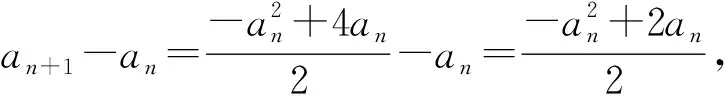
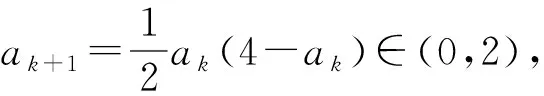
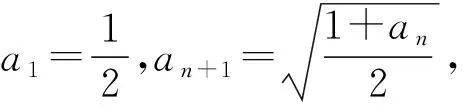
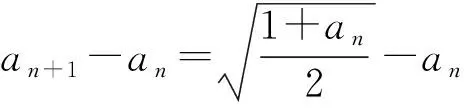
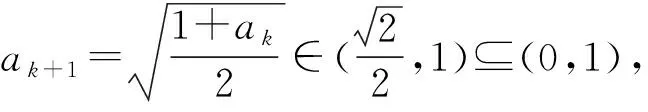
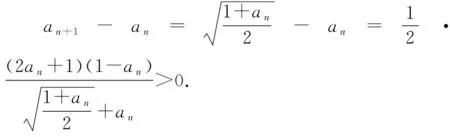
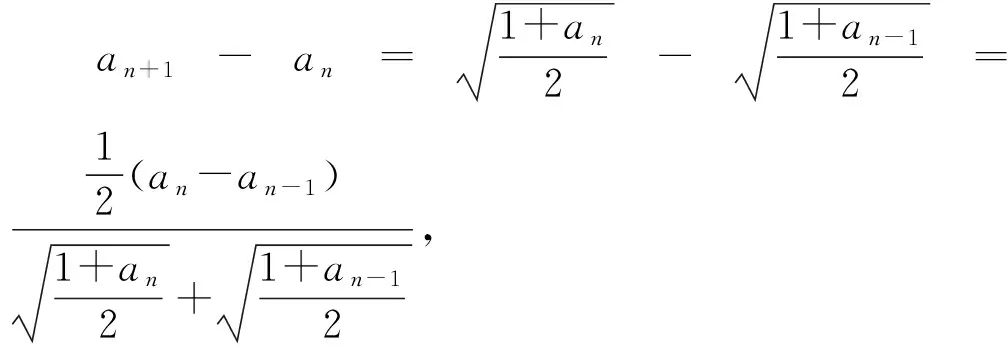
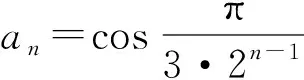
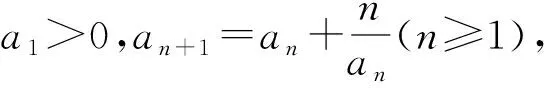
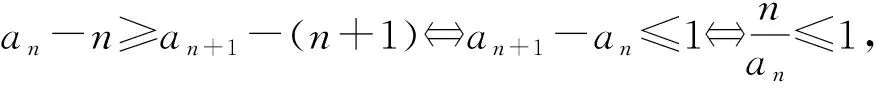
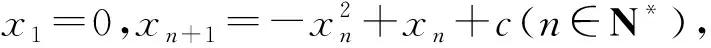
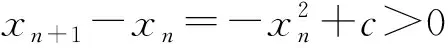
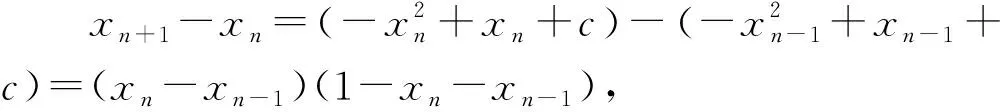
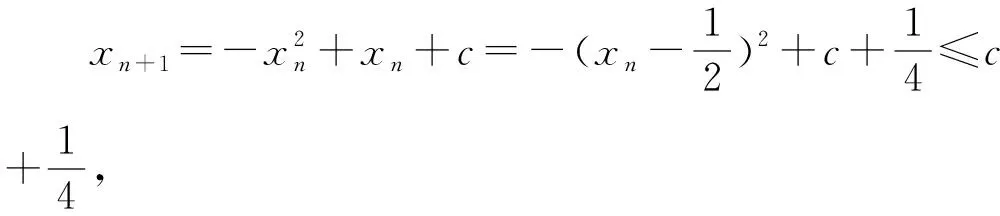
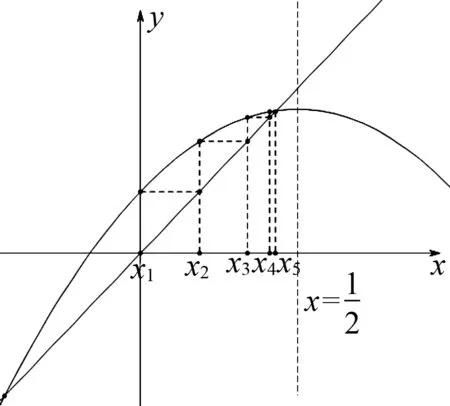
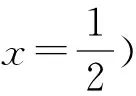
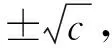
3.觸類旁通
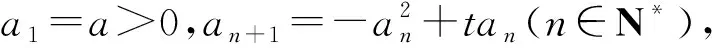
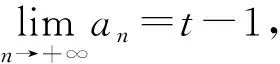
4.方法提煉