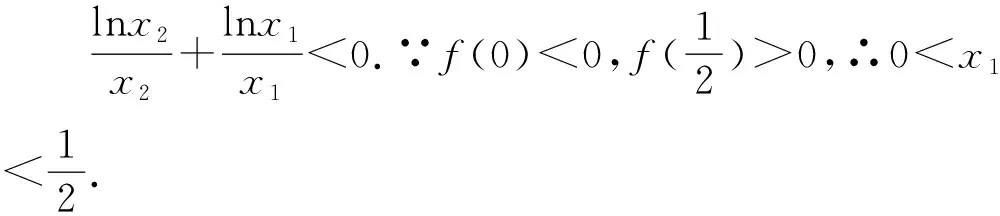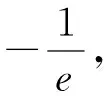同構對偶巧化簡 數形結合感直觀
——以2022年新高考Ⅰ卷第22題為例
廣東省華南師范大學附屬中學 (510630)
羅 麗
2022年新高考Ⅰ卷試題更加開放靈活,優化了情境設計,適當增加了應用性和創新性的試題,體現出對學生數學核心素養的全方位考察.高考命題加強對數學思想方法的考察,22題考察函數與方程、數形結合、分類討論、轉化與化歸的數學思想.該題構思新穎,結構精巧,本文從多層次、多角度給出解答與推廣.
1 試題再現
(2022年新高考卷Ⅰ第22題)已知函數f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.
(1)求a;
(2)證明:存在直線y=b,其與兩條曲線y=f(x)和y=g(x)共有三個不同的交點,并且從左到右的三個交點的橫坐標成等差數列.
分析:本題考查了導數的應用,函數與方程.第一問用導數求函數的單調性,函數的最小值,然后列出方程求得a的值.第二問求函數的零點,可作出曲線函數y=f(x),y=g(x)和直線y=b的大致圖象,結合圖象分析,分別求出三個交點的橫坐標的表達式后,證明其成等差數列即可.本題第二問獨具匠心,結合方程的根與等差數列的知識,考察學生數形結合、轉化與化歸的數學思想以及推理論證能力和運算能力,巧妙運用函數同構法可以快速得出結論.
2 多解探究
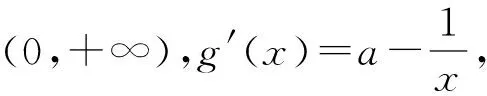
(法一)分離出lna解方程(*)式.
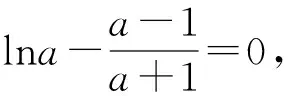
(法二)簡單變形解方程(*)式.
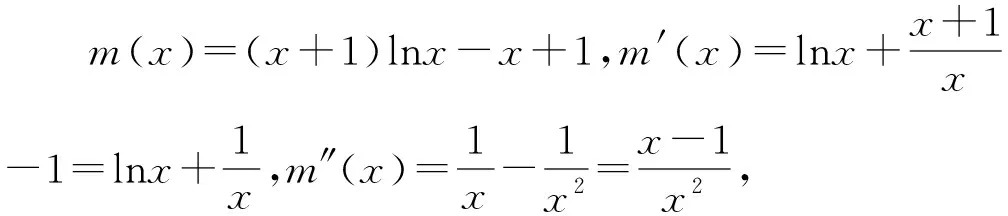
(2)(法一)代數“同構”法.

圖1
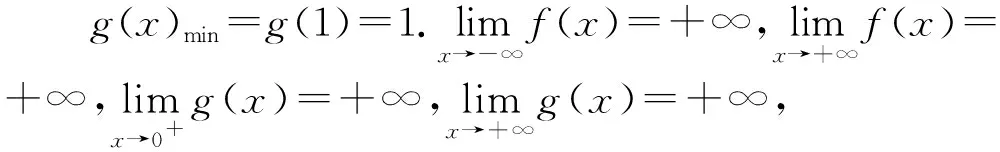
下面需證明2x2=x1+x3.
注意到f(lnx)=g(x),x>0,因此有f(lnx2)=g(x2)=f(x1),且lnx2,x1小于零,由函數f(x)(x<0)的單調性得x1=lnx2.又f(x)=g(ex),因此有f(x2)=g(ex2)=g(x3),且ex2,x3都大于1,由函數g(x)(x>1)的單調性得x3=ex2.根據x2滿足(△)式,則有2x2=ex2+lnx2=x3+x1,即從左到右的三個交點的橫坐標成等差數列.
(法二)幾何法“對偶”性質.
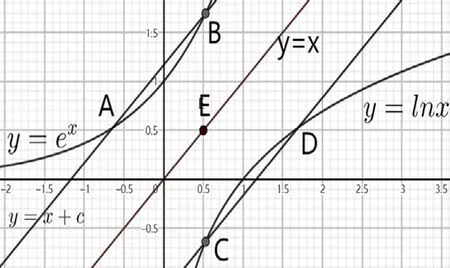
圖2

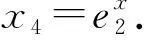
(法三)幾何矩形的性質.
交點情況和圖象與解法二一樣,下面需證明.根據對稱性,直線AC垂直于y=x,直線BD垂直于y=x,又直線AB和直線CD與直線y=x平行,則四邊形ABCD為矩形.根據矩形的對角線互相平分,則有x2+x3=2x2=x1+x4.
特別地,因為x2=x3,則直線BC垂直x軸,三角形ABC為等腰直角三角形,那么四邊形ABCD為正方形.對角線BC與AD交于點E,根據對稱性,點E在y=x上.
點評:本題第二問用了三種方法求解,法一利用了函數“同構”特點,“同構”即結構相同,根據f(lnx)=g(x),x>0和f(x)=g(ex),可以得到x1、x2和x3的數量關系,證明出等差數列的關系.法二利用“對偶”性質,充分考慮圖象的對稱性,利用數形結合的方法證明.法三在法二的基礎上利用矩形的對角線互相平分的性質進行說明,巧妙地將方程的解轉化為幾何圖象的關系.根據法三的方法,易將問題拓展到有四個交點的情形,并進行類似的證明.
3 變式拓展
吳康教授對此題拓展到有四個交點的情形,我們也用三種方法進行證明.
探究1 證明存在直線y=c,其與兩條曲線y=f(x)和y=g(x)共有四個不同的交點,并且從左到右的四個交點的橫坐標設為n1,n2,n3,n4,則n1+n4=n2+n3或n2-n1=n4-n3.
解法一:代數“同構”法.
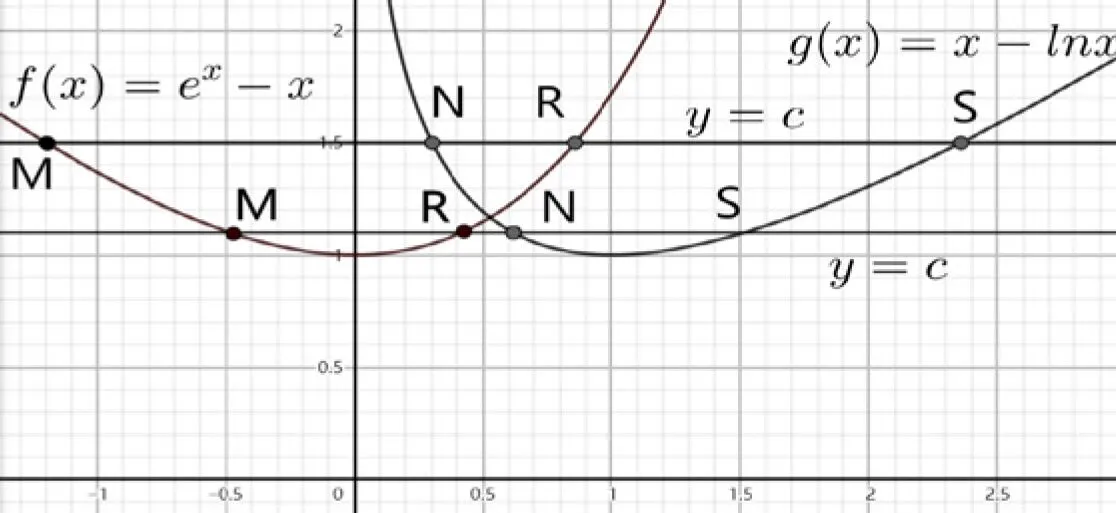
圖3
可以做出直線與兩條曲線的圖象如圖3.
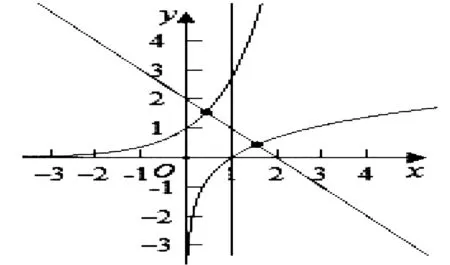
若有四個交點,則直線y=c的取值有兩種情況,一是直線y=c在直線y=b的上方,此時c>b(b=ex2-x2=x2-lnx2),從左到右交點分別假設為點M,N,R,S,其中點M和R在曲線f(x)上;二是直線y=c在直線y=b的下方且大于兩條曲線的最小值,此時1 不妨首先討論當c>b時,根據交點的情況有f(n1)=f(n3)=c,g(n2)=g(n4)=c,n1<0 當1 解法二:幾何“對偶”性質. 只討論當c>b時的情形,若1 解法三:幾何矩形的性質. 利用原題解法三的思路,知四邊形ABCD為矩形,根據矩形的對角線互相平分,則有n2+n3=n1+n4. 點評:將問題拓展到有四個交點的情形,啟發學生類比聯想,化歸轉化,數形結合的數學素養,能主動地提出問題并解決問題.利用幾何法中矩形的性質可以挖掘函數問題的本質,啟發學生多角度思考與深度思維. 探究2 當直線與兩條曲線分別有三個交點和四個交點時,試比較n2+n3與2x2的大小.(四個交點時,中間兩個點的橫坐標為n2,n3;三個交點時,中間點的橫坐標為x2,x2≈0.527,b≈1.167) 結論當c>b時,n2+n3>2x2;當1 當1 點評:類似極值點偏移的做法,構造偏差函數h(x)=f(2x2-x)-g(x),轉化為分析函數恒成立的問題.對于兩個函數比較交點的大小,本質上考察函數的對稱性和增速,可以通過構造偏差函數,將二元問題轉化為一元問題處理.判斷大小關系可以由極端情況進行推理,當c→∞時,n2→0,n3→∞,顯然有n2+n3>2x2.當c→1時,n2→0,n3→1,則有n2+n3<2x2. 例1 (多選題)已知函數f(x)=ex+x-2和g(x)=lnx+x-2的零點分別為x1,x2,則下列結論正確的是( ). A.x1+x2=2 B.x1lnx2+x2lnx1<0 分析:解決雙變量問題的常規思路是轉化為單變量問題,本題利用對偶特點和數形結合的方法,也可以巧妙得到答案為ABD. 圖4 A選項正確.由f(x)=ex+x-2=0得ex=2-x,由g(x)=lnx+x-2=0得lnx=2-x,作出函數y=ex,y=lnx,y=2-x的圖象如圖4: 由y=ex的反函數y=lnx關于直線y=x對稱,y=ex與直線y=2-x的交點為(x1,2-x1),y=lnx與直線y=2-x的交點為(x2,2-x2),可得x1=2-x2,即x1+x2=2. 在高中教學中,一題多解并非“炫技”,希望通過不同角度的解答方法啟發學生的數學思維.一題多變探究式教學,激發學生提出問題并主動研究,能夠透過現象看本質,厘清同類問題的解題思路,站在命題人的角度看問題.對于函數與導數的模塊,學生待突破的難點是如何處理復雜的計算問題并將相關條件轉化,教師在教學中應滲透數形結合、等價轉化、從特殊到一般等數學思想方法,從而提升學生的數學推理、數學運算等核心素養.數學探究類題型越來越受到命題者的重視,這也將加快數學教學模式的轉變,使探索發現成為日常教學的新常態.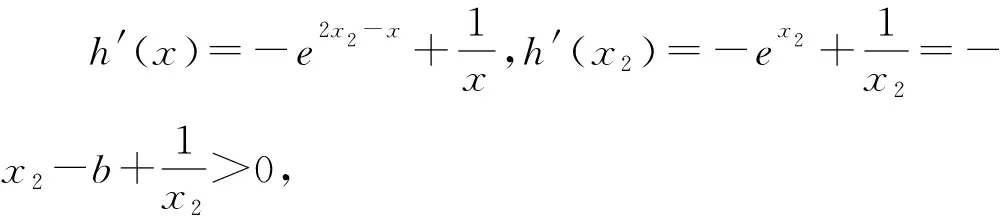
4 觸類旁通