Nesbitt不等式的一個新推廣及引申

山東省鄒平雙語學校 (256200)

姜坤崇 高奇媚

這是一個對稱、簡潔、優美、內涵豐富、應用廣泛的經典不等式，歷史上曾作為1963年莫斯科數學競賽題出現過，對它的研究(如證法、推廣、加強、加細、應用等)也歷久不衰，文獻[1]給出了它的一種新推廣，本文給出它的一種新推廣.

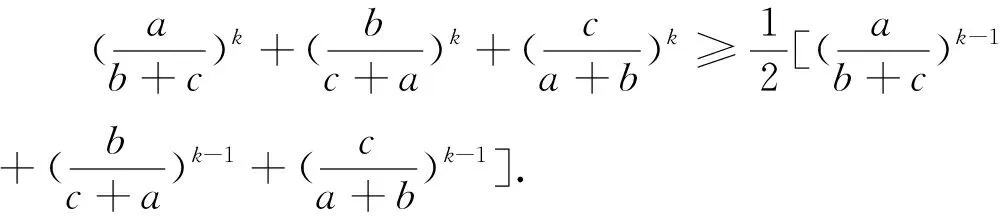
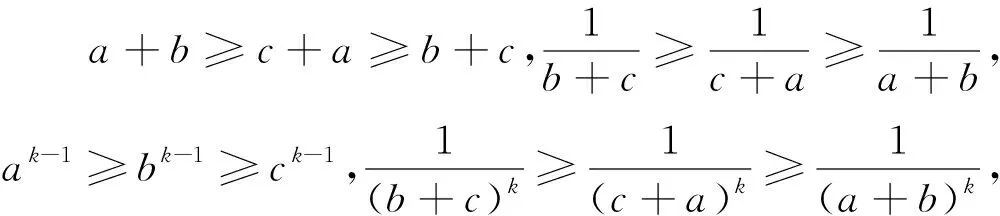
在不等式②中令k=1即得不等式①，所以不等式②為不等式①的一種推廣.

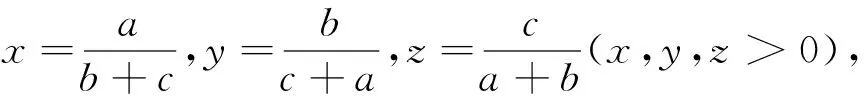
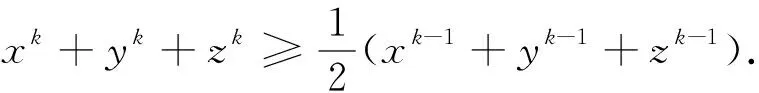
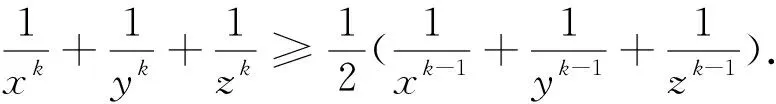
命題1中的不等式②是關于三個正數a,b,c的不等式，若將它推廣為n(n≥3)個正數的不等式，則有如下命題4成立.

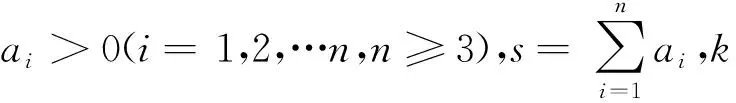
證明從略.

同樣的，命題2、3中的不等式也可以推廣到n(n≥3)個正數中去，有如下的兩個命題成立.

命題5 設xi>0(i=1,2,…,n,n≥3),且

命題6 設xi>0(i=1,2,…,n,n≥3),且

以上兩個命題的證明均從略.

由命題1，我們可得一個有趣的無窮長的代數不等式鏈：

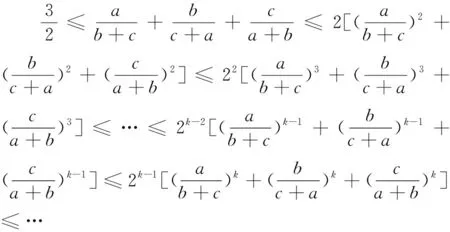
同樣，由命題2、3可分別得另兩個無窮長的條件不等式鏈：

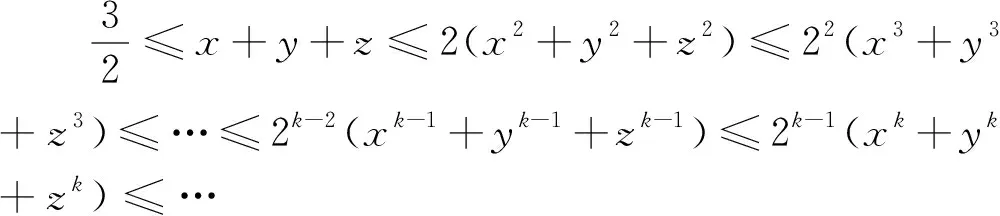
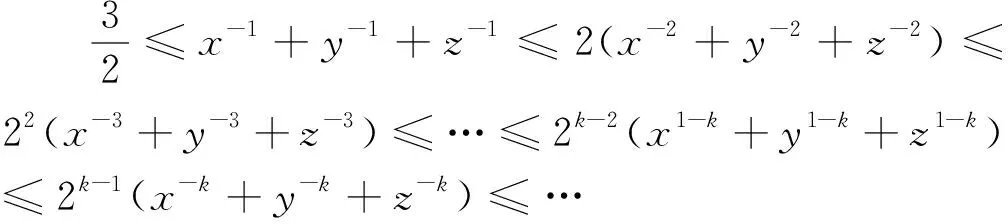
由命題8、9，我們也可得任意多的特例不等式.由命題4、5、6我們也可以分別得到無窮長的不等式鏈和無窮多的特例不等式，限于篇幅，這里不再給出.