基于可視化教學的解題研究
——對一道預賽題的思考與探源

廣東省佛山市南海區第一中學 (528200)

徐守軍

古有朱熹《觀書有感》云：“半畝方塘一鑒開，開光云影共徘徊.問渠那得清如許，為有源頭活水來.”筆者結合自身輔導競賽的經歷，一直在思考，如何讓課堂清新如許，學生心有靈犀？競賽試題難度上高于高考，卻離不開高考，技巧性強，但大多數時候最后落葉歸根，追本溯源，都可以回歸到高考試題的常規解法中，細細體會，讓思維可視化，還可以撥開云霧，看透實質，使得問題原形畢現.本文以一道2018年浙江預賽試題為例予以探析.

1.題目呈現

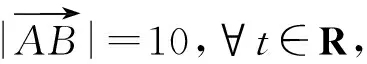
2.問題求解

2.1 思維過程可視化

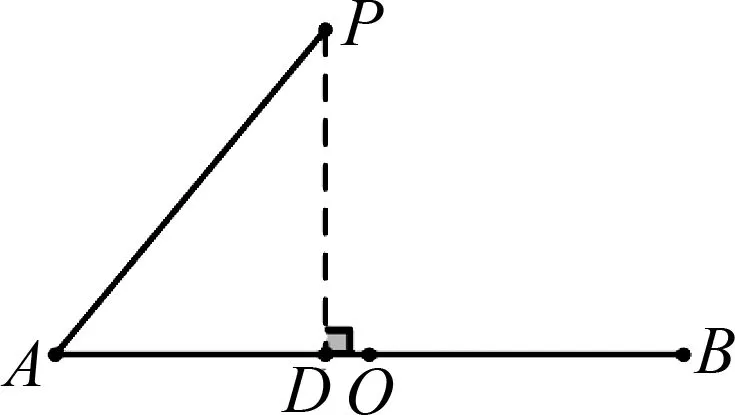
圖1

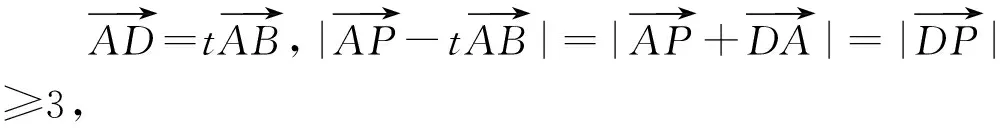
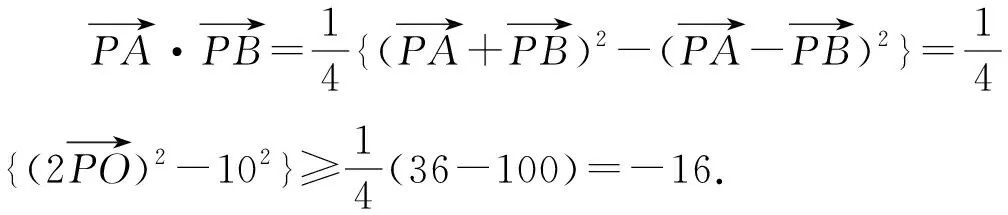
圖2

解法二：如圖2，設∠APB=θ，PA=x，PB=y，依題意可知PD⊥AB，且PD=3.由三角形面積公式得xysinθ=30,由余弦定理得x2+y2-100=2xycosθ.化簡代入得

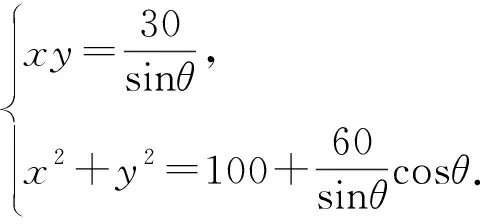
圖3

2.2 知識關聯可視化

2.3 題目探源可視化

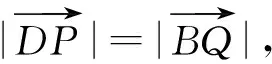
對于這種問題，涉及到平面上矩形內部求內積的動點問題，學生會首先想到建立平面直角坐標系.這是常用的方法，建系設點，利用函數的觀點求最值.在此基礎上，學生對于本文中的這道預賽題就會有新的體會，可以給出下列解法：

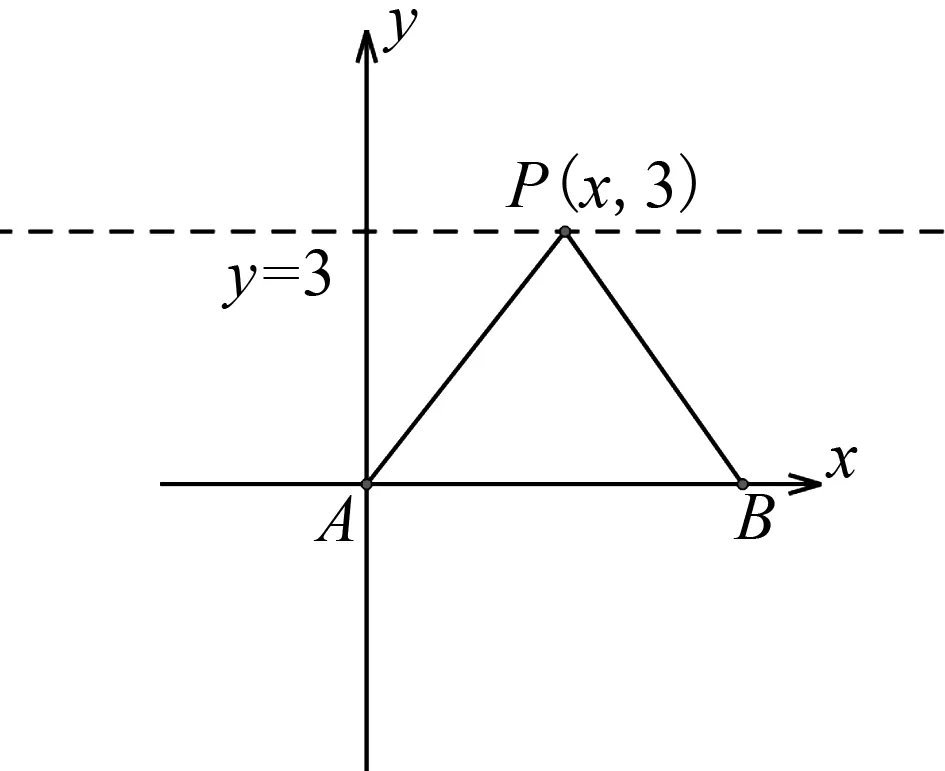
圖4

設PA=a，PB=b，

∠APB=θ，則S△PAB=

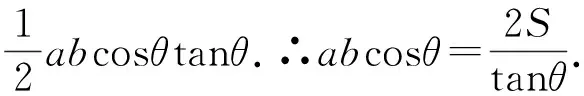
到此，問題的本質就清晰可見.就是平面上動點到定直線的位置關系，最后只轉變成θ一個變量進行討論，使得問題變得簡單明了.

3.教學反思

透過現象看本質是解題的基本能力和要領.正如羅增儒老師所說：“對題目的結構，不僅注重外形上的分析，而且注重內容上的理解，能從一個孤立靜止的數學形式中找出關聯活動的數學內容.方法是對內容的理解，方法寓于概念之中.”數學競賽不僅考查學生的能力，也考查學生的思維，而數學問題萬變不離其宗，思想方法之間有千絲萬縷的聯系，在教學上不僅要教給學生解題的技巧與方法，還要教會學生學會思考，學會挖掘，學會把問題簡單化，把數學問題進行轉化，注意從內容的聯系上尋找解題思路，才能使思維的高度更上一層樓.