對一道幾何最值問題的探究*

安徽省合肥市第一中學 (230601)

涂成浪 谷留明(指導教師)

一、初識題目

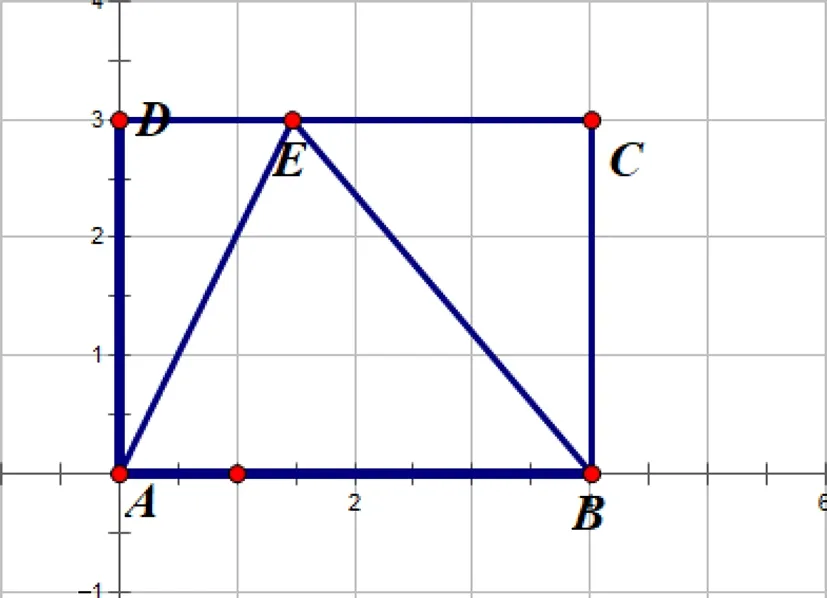
圖1

題目在矩形ABCD中,AD長為3,AB長為4,動點E在矩形ABCD的四邊上運動,如圖1，求點E到點A和點B的距離之和的最大值？

初看這道題時,以為只需簡單地作一個對稱,再利用三邊關系求解,但發現此題求的是最大值,并非常見求最小值問題.經過簡單的分析,容易確定所求線段和最大時,點E應在線段CD上,下文中只分析這種情況,且點E不在線段CD兩端.根據直覺,覺得當點E應該在與點D或點C重合時,所求線段和取得最大值.

為了嚴謹地求出最值,先利用函數來對線段和進行表達,然后求出它的最大值.

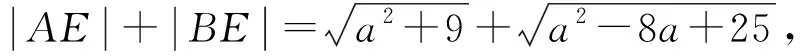
二、討論交流

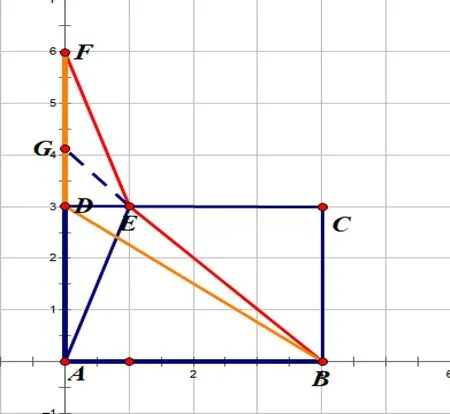
圖2

經討論之后便出現了兩種簡單且巧妙的方法.我們從幾何角度來考慮這個問題的.下面只分析點E在線段AB上(不含兩端)時的情況,證DA+DB>EA+EB.

方法一：如圖2：作點A關于點D的對稱點F,連接BD,FE.延長BE交DF于點G.此時,DA+DB=FD+DB=FG+GD+DB>FG+GB=FG+GE+BE>FE+BE=EA+EB.

運用此法,可以證明隨著點E從線段AB中點向點D靠近時,EA+EB逐漸變大.當點E與點D或點C重合時,EA+EB取到最大值8.

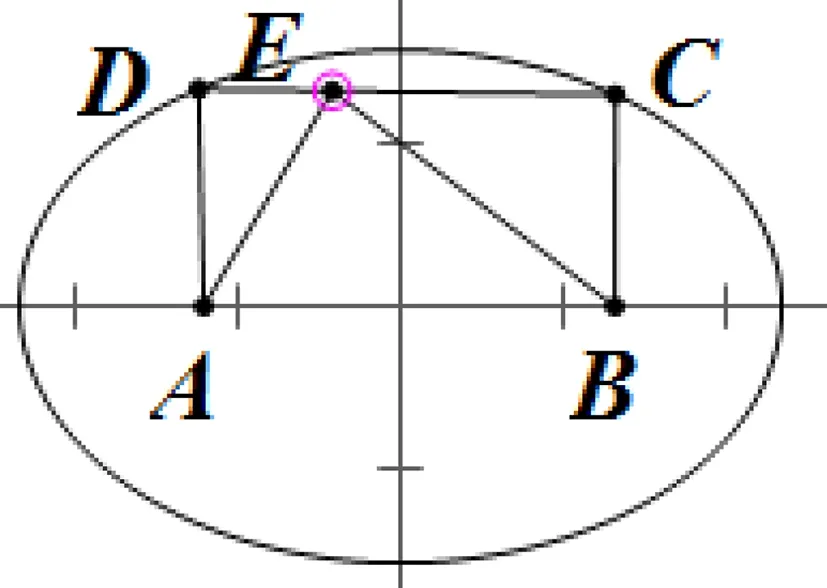
圖3

方法二：如圖3,構造一個以點A,B為焦點,長軸長為DA+DB=8的橢圓,在上半橢圓上取點D,C,使四邊形ABCD為矩形.結合圖形得線段CD上兩點之間的點都在橢圓內,所以EA+EB<8=DA+DB.故當點E與點D或點C重合時,EA+EB取到最大值8.

以上兩種方法都是從幾何角度來思考這個問題的.方法一從三邊關系來證明不等式,方法二構造橢圓,利用橢圓的第一定義來轉化邊,類似于根據點在園內,得到該點到圓心的距離大于半徑.

三、“自我斗爭”

雖然以上兩種幾何方法已得出結果,是否可將代數與幾何相結合來解決這個問題？于是經過一番思索,我得到了以下數形結合的方法.

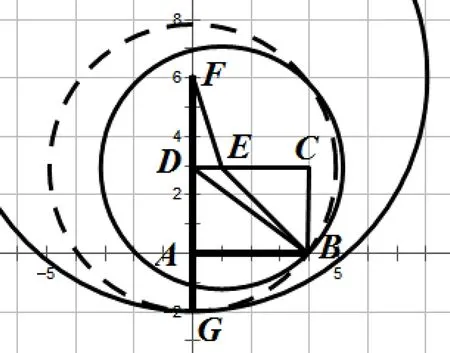
圖4

目標是證明DA+DB>EA+EB,即證FD+DB>FE+EB,即證FG>FE+EB.如圖4建系,設E(a,3)(0

相比于一般求最值的題目,本題難點在于求兩條線段的和,這個方法的基本思路在于用圓的半徑等長,將折線段轉化為一條直線段,然后將要證的大小關系,轉化為兩圓的位置關系.