基于表征的數學問題解決策略探究*

廣東省中山市第二中學 (528400)

陳姍姍

數學問題的解決過程就是對問題的表征過程，不同的表征有著不同的功能，提供不同的信息，良好的問題表征有助于學生生成問題理解、減輕認知負荷、構建解題策略.美國著名的認知心理學家和人工智能的創始人西蒙也曾指出，“表征是問題解決的一個中心環節，它說明問題在頭腦中是如何呈現的，如何表現出來的.如果一個問題得到了正確表征，可以說它已解決了一半”.[1]因此，在教學中要重視多元表征的教學策略.

一、影響數學問題解決的原因分析

數學學習的過程就是問題解決的過程，如何有效地解決問題？首先是審題，然后對問題進行表征，最后根據適宜的表征構建解決問題的策略.在這一過程中對問題進行表征是關鍵，表征是問題解決的切入點，但是不少學生面對問題時，無法對問題進行表征，往往表現出表征識別能力低，表轉換意識弱.

1.表征識別能力低

表征識別能力的培養是一個長期的過程，每一種表征形式的特點和功能需要長期在對問題的表征中逐漸掌握，由于學生追求答案，為解題而解題的習慣導致很多很好的多元表征問題的機會錯失.從而對問題的多元表征識別能力得不到提高，不能準確快速地識別題目中的原有表征以及目標表征的意義.另外，對問題僅停留在初始表征，即對概念、定理、公式等進行表征，而深層表征即對已知問題信息進行翻譯和轉換較少，從而導致表征識別能力低下.

2.表征轉換意識弱

在問題解決過程中受阻的原因很多，但是“一條道走到底”是其中一個最重要的原因，部分學生在對問題表征時總是停留在一種形式，沒有強烈的對問題多元表征的意識，表征間的轉換或轉譯意識淡薄，總是容易受原有表征和目標表征的定勢影響，不善于借助其他表征.比如集合的交并補僅從文字表征理解起來有點費力，但是借助圖形表征“韋恩圖”則可以起到“豁然開朗”的效果.

二、表征在問題解決中的重要性

問題解決前對問題的表征形式是很重要的，只有恰當的表征問題，才能從題目中提取有效信息，確定求解目標，從而激活正確的圖式理解整個問題.[2]通過對問題的表征可以生成問題理解、減輕認知負荷以及構建解題策略.

1.生成問題理解

同樣一個問題不同的表征就是對問題的不同理解，通過不同形式的表征才能比較精準地識別問題的本質.比如復數的模可以表征為向量的模，還可以表征為距離，也可以從數的角度識別成絕對值，一種表征形式就加深一層理解，在解決問題時就會多一種問題解決的策略.

2.減輕認知負荷

不同認知風格的學生對問題表征的能力是有差異的，學生可以根據自己的認知習慣和認知水平選擇適合自己的問題表征形式，也可以通過不同的表征從不同的角度對問題進行認知，在一定程度上大大減輕了認知負荷.比如空間幾何中線面關系的定理和性質，每一條定理和性質都有三種表征形式，學生可以選擇文字表征、符號表征或者圖形表征對定理和性質進行理解.可以說多元表征是減輕認知負荷的最好載體.

3.構建解題策略

問題解決的心理過程可大致分為兩個層次，一是理解問題，其中包括對問題的轉述和問題表征.即將問題用語言或符號表示出來，并轉化為學習者的內部心理表征；二是執行計劃，其中包括計劃的執行與反饋監控.由此表明，良好的問題表征及恰當的轉換是問題成功解決的前提和關鍵.[3]表征選擇和表征轉換決定了問題解決策略的路徑，以復數為例，把復數表征成向量就用向量知識解決，表征成點就用幾何知識解決，表征成數就用代數知識解決.

三、基于表征的數學問題解決策略

學生面對一個問題時首先是思考如何理解題意，而很多題目僅從已知條件的外在結構是很難清晰地知道它的內在特點，這就需要對問題進行多元表征，選擇哪種表征形式直接決定了問題能否順利解決.高中數學問題解決中常見的表征形式有三種：圖形表征、符號表征和文字表征.靈活應用三種表征，熟練三種表征之間的轉譯是解決數學問題的關鍵.

1.圖形表征：讓問題可視化

數學問題的解決過程中很多意想不到的錯誤就是缺少問題可視化的過程，除了上述提到的學生受表征能力的影響外，還有一個重要的原因就是思維定勢導致的表征轉換的偏向性，多數學生偏向數學符號的表達，而不太習慣繁瑣的文字表征以及圖形表征，而圖形表征的最大優勢在于直觀，讓問題可視化.通過把問題可視化更有利于分析問題和解決問題.

題1 在復平面上，一個正方形的三個頂點按順序分別對應的復數是1+2i,-2+i,0，那么這個正方形的第四個頂點對應的復數為( ).

A.3+iB.3-iC.1-3iD.-1+3i

這道題的出錯率很高，大多數學生選了A，除了受思維定勢的影響之外，更多的是學生在解題時沒有對題目中“三個頂點按順序分別對應的復數是1+2i,-2+i,0”進行圖形表征，而是憑著以往的解題經驗，默認這三個點分別是相鄰的，如果正方形是ABCD，那么就默認這三個點就是A、B、C，這樣做出來的選項是A，如果作圖則求出的答案是D.但是對于選項A作圖可以看得出是不能構成正方形，那為什么那么多人會選擇A？原因肯定不僅僅是學生沒有對結果通過作圖進行驗證，而是對題目的理解出現了偏差.一是對文字語言的理解受思維定勢的影響，平時做過不少類似的題目，如人教版必修二81頁的第5題：四邊形ABCD是復平面內的平行四邊形，A,B,C三點對應的復數分別是1+3i,-i,2+i，求點D對應的復數.這里A,B,C對應的三個點就是按順序的，而題1中的三個點顯然不是按順序的，二是學生的惰性思維和惰性行為導致，懶得作圖，心算來得比較直接，思維不嚴謹，認為這是一道比較基礎的題.在做錯的學生中基礎好的學生占比較多，相反數學基礎一般的學生反而正確率比較高，原因很簡單，就是基礎一般的學生在做題時按部就班地根據題意畫出圖形，再根據圖形表征進行解答，而基礎較好的學生直接根據題意進行解答.事實上，作圖的過程就是思維可視化的過程，通過圖形表征讓問題直觀地呈現出來，以形解數，以數解形，思維更嚴謹，這樣會少走很多彎路，也會提高正確率.

2.符號表征：讓問題清晰化

符號表征有著簡潔的特點，是數學學習的主要語言，也是學生最熟悉的語言，但是符號表征同時有著高度抽象的特點，符號識別能力弱的學生很難從外在結構找到問題的切入點.因此，應根據所學知識把難以識別的符號轉譯成便于理解的符號.當然，轉譯并不是一步到位，有的時候需要多次轉譯，但是在不斷地轉譯的過程中就會對問題的理解逐漸清晰，從而才能構建出優良的問題解決策略.

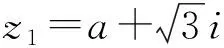
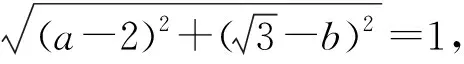
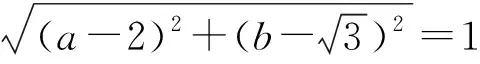
3.文字表征：讓問題結構化

分析問題首先應該從問題的結構入手，剖析問題的結構有利于發現問題的本質，從而對問題進行適宜的表征.但是由于學生表征具有偏向性，對于數學學習來說，學生較為喜歡符號表征與圖形表征的轉譯，而忽視對文字表征的重視.其實如果對數學對象的意義能夠用精準的文字表述出來數學素養是很高的.因此，數學問題的解決中要加強對語言表征的轉譯.

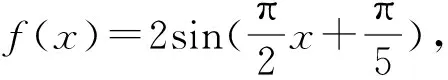
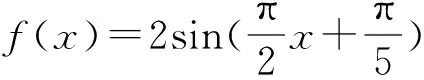
在對符號表征進行轉譯的過程中就是對問題的結構進行剖析，每轉譯一次，結構就優化一次，在兩次的轉譯中問題的結構變為兩個并列式的關系，一是求函數的最小值，二是求函數的最大值.根據這兩個結構化的問題，根據目標表征|x1-x2|進行第三次轉譯“求函數取得最值時的x的取值之間的距離”.不少學生在解題時不會分析題目中的關鍵信息，其原因之一就是沒有對關鍵信息進行表征之間的轉譯，轉譯的過程就是復雜問題簡單化、抽象問題具體化的過程，題1中抽象的數學符號f(x1)≤f(x)≤f(x2)其實就是隱含著函數的最值問題，要對不理解的信息結合題干反復讀，一步步轉譯，才能挖掘出題干中的隱藏信息.在轉譯表征的過程中逐漸剖析問題的結構，一層層打開題目背后神秘的面紗.這道題看似簡單，但是思維的路徑很長.學生在做此題時被符號f(x1)≤f(x)≤f(x2)給迷惑了，思考的重心在這個不等式，而忽視了關鍵詞語“任意”和“都”.學生一般會受題干中原有表征的影響，缺乏轉譯表征的意識，問題以何種表征出現，學生就用何種表征解題.沒有多元表征的相互轉譯，解題思路顯得非常狹隘.很顯然這道題只有把這兩個詞“任意、都”放進思考的路徑中，并對其進行更進一步的文字表征轉譯才能理解這道題的意思.

新高考最大的變化就是對學生思維能力的考查，繁瑣的運算不是主要考查的目的，對題目信息的多元表征才是命題者的重心.單一的表征往往是不足以解決數學問題的，很多時候三種表征交替出現，互相補充，不同的表征發揮著不同的作用，在不同的表征轉換中生成數學理解.