例析“角平分線”在思路探究中的作用

?甘肅省武威市天祝藏族自治縣新華中學 趙 霞

1 引言

經歷了幾何解題思路探究的過程后，人們通常會發現到找出解題的突破口非常關鍵[1].基于此，本文中借助幾道例題分析“角平分線”對初中幾何解題思路探究發揮的作用，希望對一線教師有所啟發.

2 例題引入，思路探究

例1如圖1，已知在Rt△ABC中，∠ACB=90°，∠B=60°，AD平分∠BAC，CE平分∠BCA，AD與CE相交于點F，FM⊥AB，FN⊥BC，垂足分別為點M，N.求證：FE=FD.

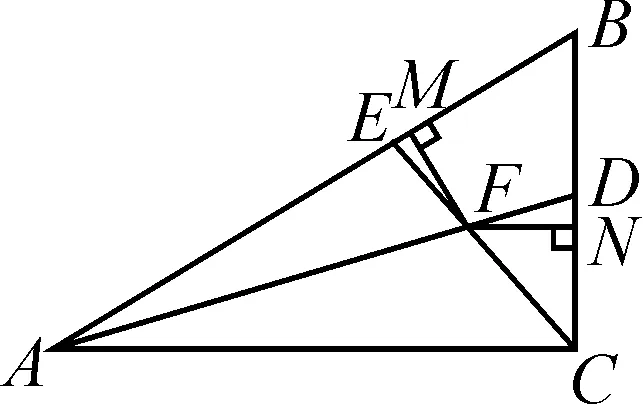
圖1

分析：本題可根據題目已知條件及角平分線定理作出點F到AC的距離，如圖2所示.然后，通過FN的“橋梁”作用證明FM=FN.最后，在證明△FME和△FND全等的基礎上得到FE=FD.

證明：如圖2所示，過點F作AC的垂線，垂足為H.

∵AD平分∠BAC，CE平分∠BCA，且FM⊥AB，FN⊥BC，

∴MF=FH=NF.

∵∠ACB=90°，∠B=60°，

∴∠MEF=75°，∠FDN=75°.

∴△FME≌△FND(AAS).

∴FE=FD.

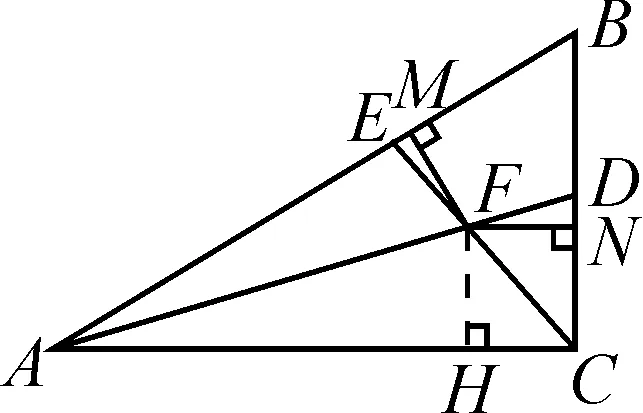
圖2

例2已知：如圖3所示，在△ABC中，∠C=90°，∠B=30°，AD是∠BAC的角平分線.求證：BD=2CD.

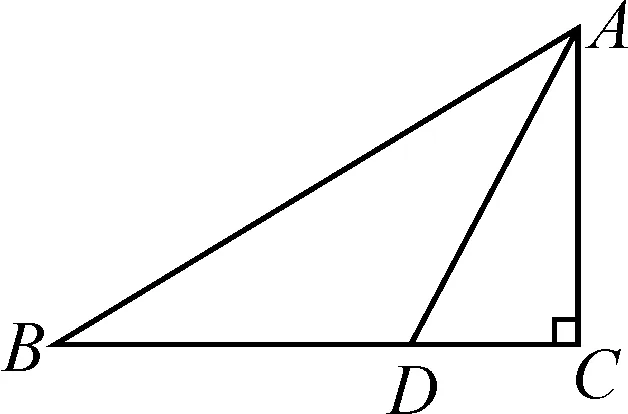
圖3

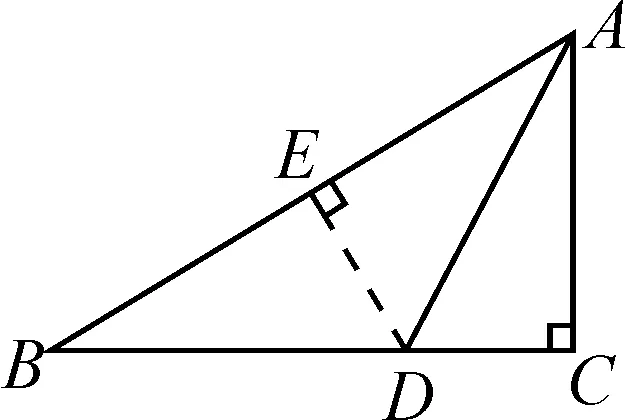
圖4

分析：本題條件不多，對尋找解題突破口最有幫助的是“AD是∠BAC的角平分線”這個條件.這類題和角平分線的性質有關，常結合等腰三角形、垂直平分線、直角三角形30°角的性質定理等知識，相對比較基礎.

證明一：∵∠C=90°，∠B=30°，

∴∠BAC=60°.

∵AD是∠BAC的角平分線,

∴∠BAD=∠CAD=30°.

∴BD=AD，AD=2CD.

∴BD=2CD.

證明二：如圖4，過點D作AB的垂線，垂足為點E.

∵AD是∠BAC的角平分線，

∴CD=ED，∠BAD=∠CAD.

∵∠C=90°，∠B=30°，

∴∠BAC=60°.

∴∠BAD=30°.

∴AD=2ED.

∵∠B=∠BAD=30°，

∴BD=2ED.

∴BD=2CD.

例3已知：如圖5所示，△ABC的外角∠CBD和∠BCE的角平分線分別是BF，CF，且這兩條角平分線相交于點F.求證：點F在∠DAE的角平分線上.

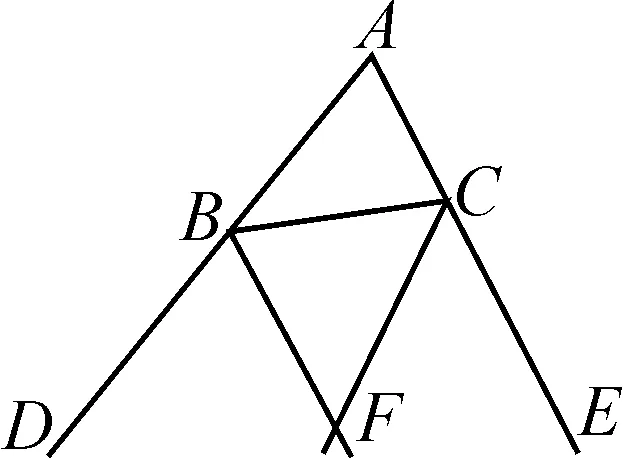
圖5

分析：本題給出的條件非常少，但當已知角平分線時，不妨將角平分線上的點到角的兩邊的垂線段作出來，然后結合“角平分線的判定定理”證明“點F在∠DAE的平分線上”.但是，要注意說明點F在∠DAE的內部，這是角平分線判定定理使用的前提.由此可見，抓住“角平分線”這個關鍵條件并借助它的性質解決問題非……