一類定邊對定角問題的解法探究

?安徽合肥一六八陶沖湖中學(xué) 武前煒

1 引言

三角形中的有關(guān)線段計(jì)算是平面幾何常考試題，常常利用勾股定理、相似性質(zhì)或三角函數(shù)來計(jì)算，不同的方法計(jì)算難易程度不一樣.

2 解法探究

下面通過兩個(gè)例題對定邊對定角問題進(jìn)行解法探究.

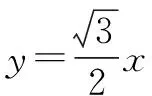
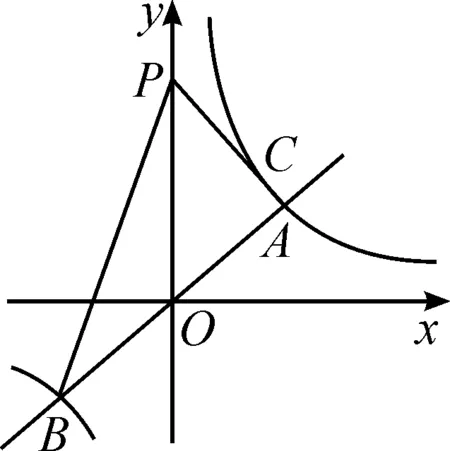
圖1

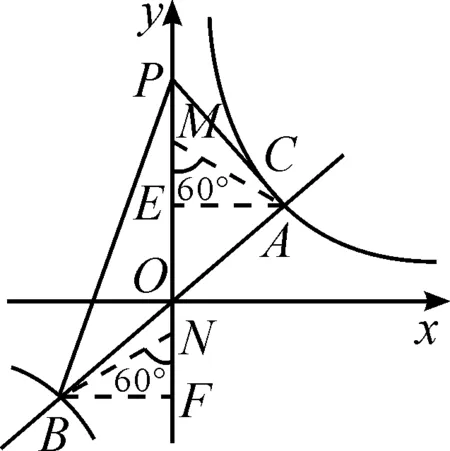
圖2

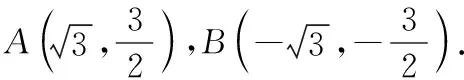
解法1：(一線三等角相似)如圖2，在y軸上分別取點(diǎn)M,N,使得∠AMO=60°,∠BNP=120°,由“一線三等角”可得△APM∽△PBN.分別過點(diǎn)A,B作y軸垂線，垂足為點(diǎn)E,F.

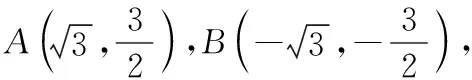
ME=NF=1,AM=BN=2.

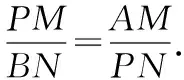
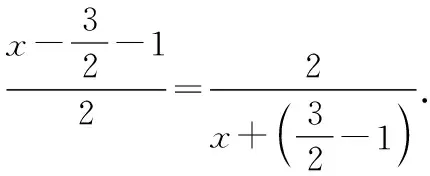
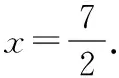
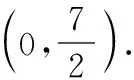
解法2：(三角形面積)設(shè)點(diǎn)P(0,y)，y>0.

由距離公式可得，

根據(jù)三角形鉛錘公式面積計(jì)算,得

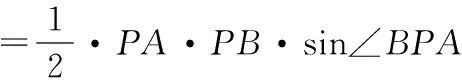
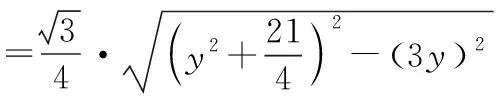
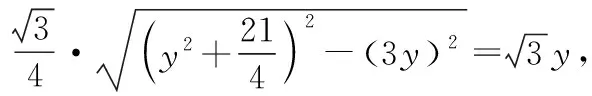
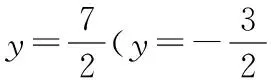
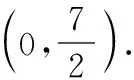
解法3：(輔助圓)先來看基本圖形，如圖3，△ABC中，定邊AB所對的∠C為定角α.

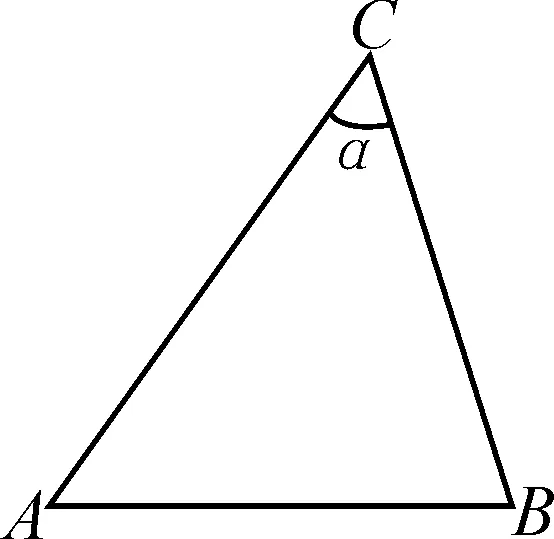
圖3

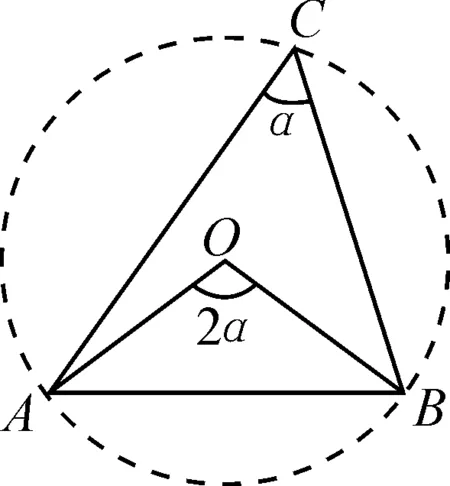
圖4

由圖形定邊對定角，考慮△ABC外接圓⊙O，如圖4，根據(jù)圓周角性質(zhì)可知∠AOB=2α，于是問題轉(zhuǎn)化為在等腰三角形AOB中來解決.特別地，一些題目中α取一些特殊角度，從而△AOB為特殊的等腰三角形，極大地方便后續(xù)計(jì)算.

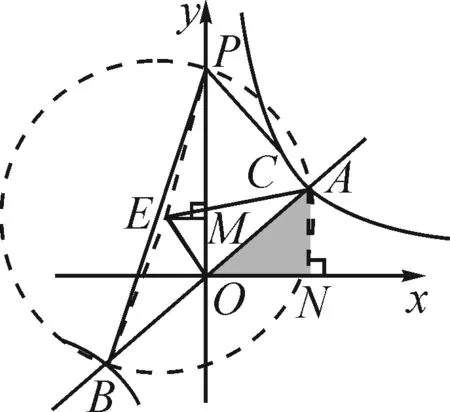
圖5

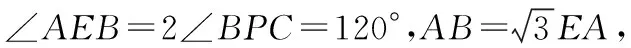
根據(jù)反比例函數(shù)的對稱性可知，點(diǎn)O為線段AB的中點(diǎn)，從而

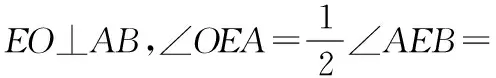
過點(diǎn)A作AN垂直于x軸，垂足為點(diǎn)N，過點(diǎn)E作EM垂直于y軸，垂足為點(diǎn)M.

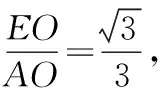
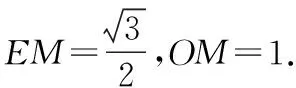
在Rt△EMP中，由勾股定理得

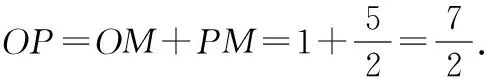
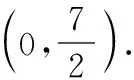
解法4：(正切和角公式)站在高中視角下，本題無需構(gòu)造，直接列式建立等量關(guān)系計(jì)算.

如圖6，分別過點(diǎn)A,B向y軸作垂線，垂足分別為點(diǎn)E,F.

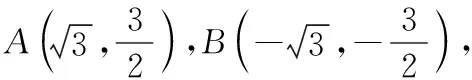
設(shè)∠BPO=α,∠APO=β,則α+β=60°.

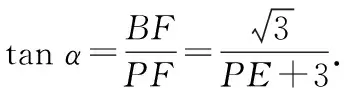
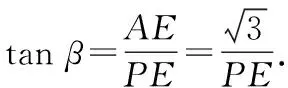
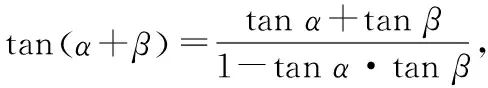
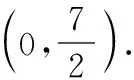
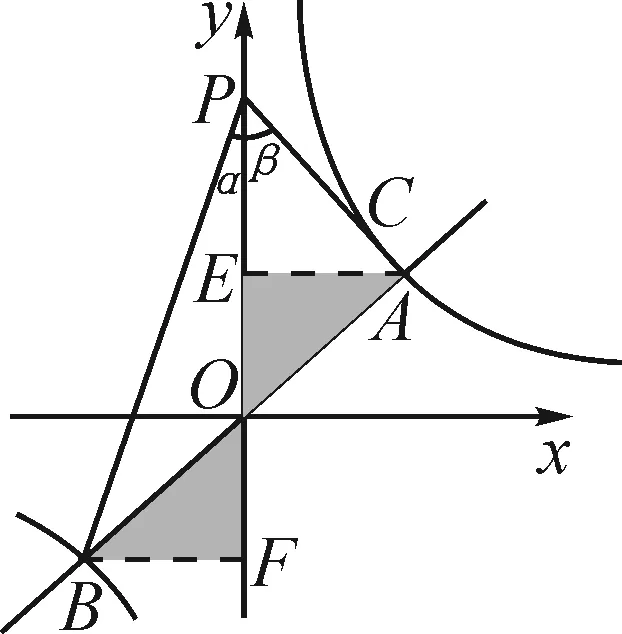
圖6

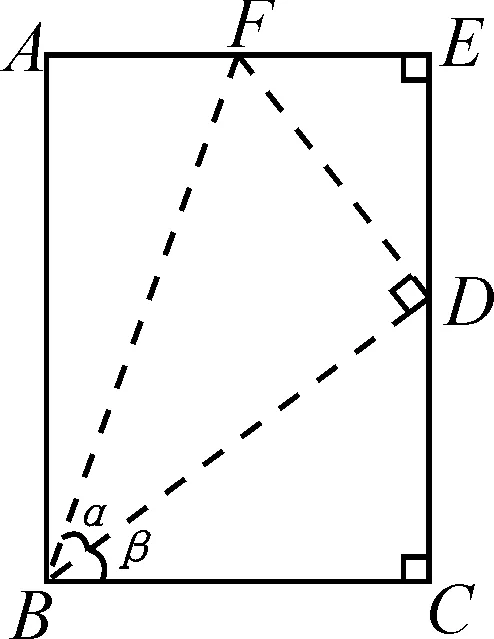
圖7

拓展：初中生通過構(gòu)造三角形相似可以進(jìn)行正切和角公式的推導(dǎo).如圖7，在矩形ABCE中，點(diǎn)D在邊EC上，點(diǎn)F在邊AE上，且FD⊥BD,連接BF，∠FBD=α,∠DBC=β.

不妨設(shè)DE=1，則EF=tanβ.

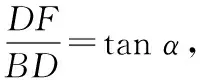
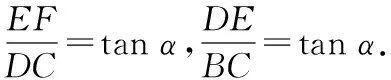
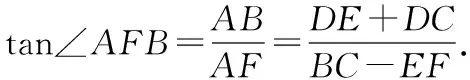
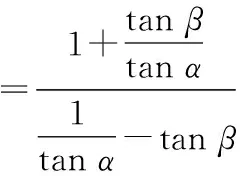
評析：合理聯(lián)想與構(gòu)造是一種重要的數(shù)學(xué)解題能力，也是平面幾何魅力所在.解題后要善于總結(jié)歸納，而不應(yīng)停留在題目本身，多琢磨其結(jié)構(gòu)，多反思其用途與變化，使其成為今后解題的工……