幾何最值問題的解題策略

?喀什大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院 陸文昊

1 引言

平面幾何背景下的最值問題，其數(shù)學(xué)原理可追溯到“兩點(diǎn)之間線段最短”“在直線外一點(diǎn)與直線上各點(diǎn)連接的所有線段中，垂線段最短”“三角形兩邊之和大于第三邊”等幾何學(xué)基本定理.蘇教版八年級(jí)上冊(cè)教科書初次介紹到“將軍飲馬”模型，即利用構(gòu)造對(duì)稱圖形來解決兩條線段和差及其延伸出的多邊形周長(zhǎng)最值問題.而我們通常認(rèn)為的“胡不歸”是以求“PA+kPB”形式的幾何最值出現(xiàn)的，通過垂直構(gòu)造直角三角形中的三角函數(shù)來處理系數(shù)k，從而完成思維上的過渡，將問題轉(zhuǎn)化至求相連兩條線段和的最值.本文將著重圍繞這兩大模型的例題展開剖析，對(duì)于更為復(fù)雜的最值模型，如“阿氏圓”“費(fèi)馬點(diǎn)”等，留給學(xué)有余力的學(xué)生繼續(xù)探究，深化對(duì)解題原理與解題思路的理解[1].

2 例題解析

2.1 構(gòu)造直角 轉(zhuǎn)化系數(shù)

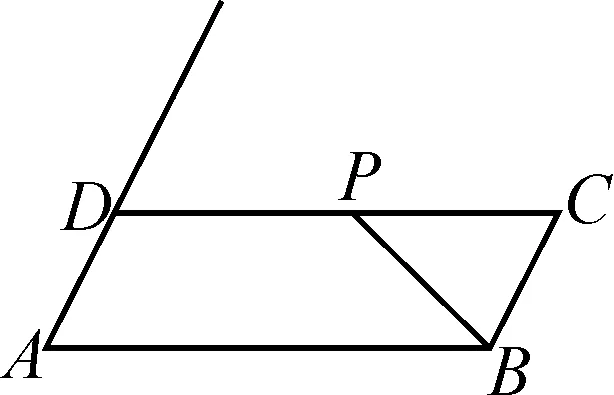
圖1

例1在ABCD中，∠DAB=60°，AB=6，BC=2，P為邊CD上的一動(dòng)點(diǎn)，則的最小值等于.

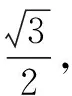
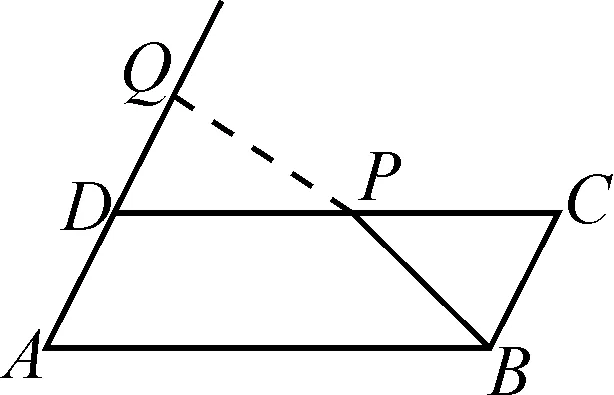
圖2

解析：如圖2所示，過邊CD上的動(dòng)點(diǎn)P作PQ⊥AD，交AD的延長(zhǎng)線于點(diǎn)Q.

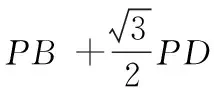
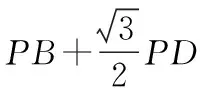
2.2 異端相接 回歸本質(zhì)

例2如圖3，在△ABC中，AB=2，∠ABC=60°，∠ACB=45°，D是BC的中點(diǎn)，直線l經(jīng)過點(diǎn)D，AE⊥l，BF⊥l，垂足分別為E，F(xiàn)，則AE+BF的最大值為.

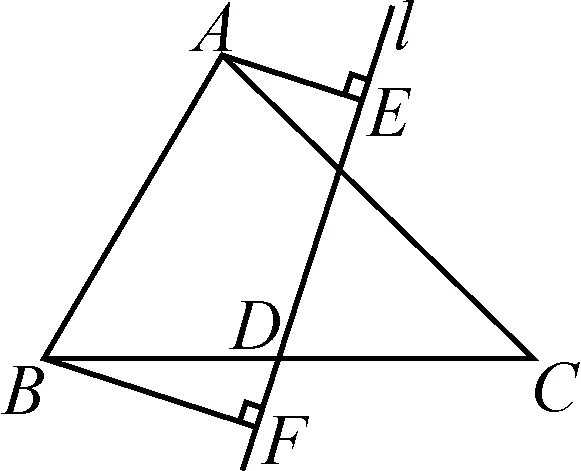
圖3

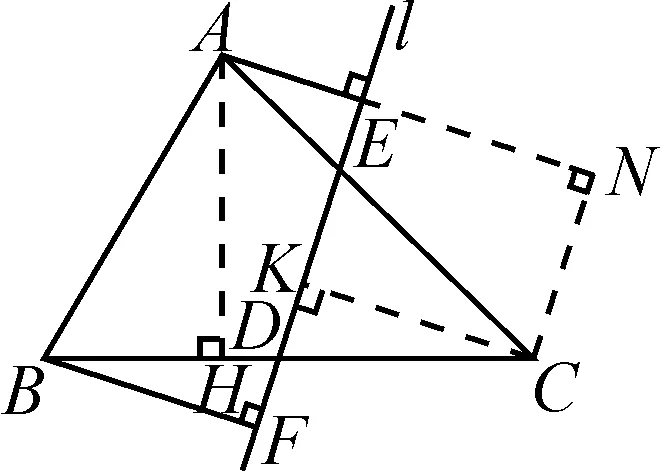
圖4

分析：初看本題，無法再?gòu)摹昂粴w”模型考慮.但無論從“將軍飲馬”還是“胡不歸”的視角考慮，所求最短路徑之和都由一個(gè)公共點(diǎn)相接，而此題的特殊之處在于兩條線段是彼此獨(dú)立.如此一來，我們不能將思路限制在兩處的線段本身，而應(yīng)通過必要的操作，將不常規(guī)的問題轉(zhuǎn)化成熟悉的情形.

解析：充分利用中點(diǎn)D，設(shè)法找出與AE相……