基于單元整體教學背景下初中數學復習課教學研究*
——以滬科版八年級上冊“角平分線復習課”為例

安徽省合肥市五十五中學 趙 瑞 吳玉情

1 引言

2021年12月，“基于‘seewo白板5’輔助初中數學幾何教學實踐研究”已進入中期評估階段，課題組成員結合課題實施研究及當前單元整體教學的雙重背景，設計了一節八年級“角平分線復習課”.本節課由筆者所在校區一位年輕老師執教，課程結束后，得到了聽課教師的一致好評.現將本節課的教學過程予以呈現，以饗廣大讀者.

2 學情分析

滬科版八年級上冊代數部分已經學習了平面直角坐標系、一次函數等相關內容，幾何部分學習了認識三角形及全等三角形、軸對稱圖形、等腰三角形等內容.通過檢測發現，所執教班級學生基礎知識扎實、水平齊整，屬于學校重點班優秀學生.

3 教學過程

師：請同學們回憶一下，什么叫做三角形的角平分線？

學生1：三角形中，一個角的平分線與這個角對邊相交，頂點與交點之間的線段叫做三角形的角平分線.

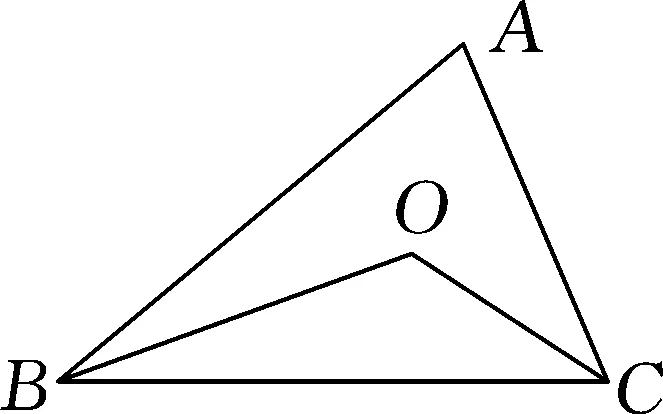
圖1

問題1如圖1，在△ABC中∠ABC與∠ACB的平分線交于點O，請探究∠BOC與∠A的數量關系.

學生2：如圖2，設∠OBC=α,∠OCB=β.

∵∠A=180°-2(α+β)，α+β=180°-∠BOC，

∴∠A=180°-2(180°-∠BOC).

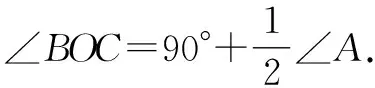
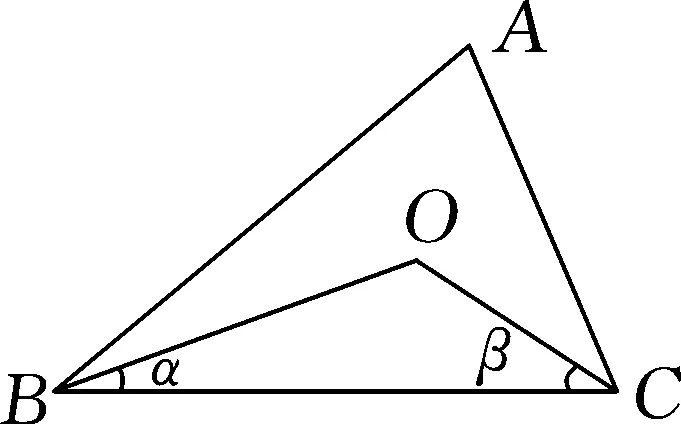
圖2

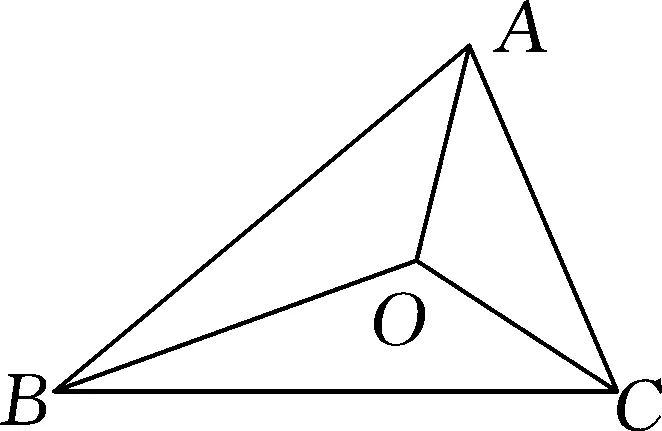
圖3

問題2在問題1的條件下，如圖3，若連接AO，AO平分∠BAC嗎？

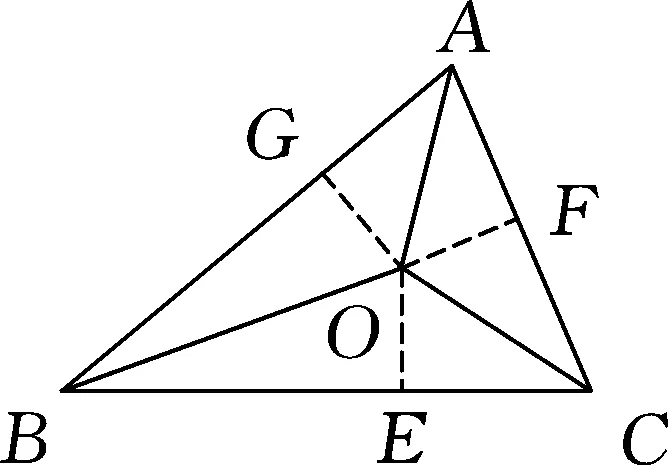
圖4

學生3：如圖4，過點O分別作OE⊥BC,OF⊥AC,OG⊥AB，垂足分別為E，F，G.

∵OB平分∠ABC，

∴OG=OE.

同理，OE=OF.

∴OG=OE.

又∵OG⊥AB,OF⊥AC，

∴AO平分∠BAC.

師：由此可見，三角形內角平分線相交于一點(三角形的內心)，且這個點到三角形的三邊距離相等.在圖3中我們同樣可以得到：

圖5

問題3如圖5，已知點O為三角形ABC的內心，且AB=7，AC=6，BC=8.若△AOB,△AOC,△BOC的面積分別與S1，S2,S3,則S1∶S2∶S3=.

學生4：如圖4,過點O作OE⊥BC,OF⊥AC,OG⊥AB，垂足分別為E，F，G.

∵點O是△ABC的內心，

∴OE=OF=OG.

∵AB=7,AC=6,BC=8,

∴S1∶S2∶S3=7∶6∶8.

變式如圖5，若O為△ABC的內心，三個角A，B，C所對的邊分別為a，b，c，△AOB,△AOC，△BOC的面積分別為S1，S2,S3,則S1+S2S3(比……