借助三角形外心 巧妙求解代數式

江蘇省海安高級中學

葉枝鳳

平面向量是歷年高考數學的一個重要知識點，是高考的熱點與重點問題之一，由于其同時兼備“形”的特征與“數”的性質，問題設置新穎多樣，內涵豐富背景創新，變化多端思維各異，是數學學科中知識與能力充分交匯與融合的理想場所，具有很好的選拔性與區分度，倍受命題者青睞.

1 問題呈現

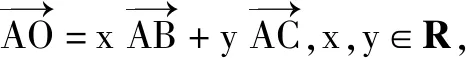
此題以三角形為載體，結合確定的三角形以及外心，通過含參數的平面向量的線性關系式的建立，進而求解對應參數的一次代數關系式的值.破解此類問題，關鍵就是要抓住平面向量中的“形”的特征、“數”的性質或“形”與“數”的和諧統一，從平面幾何角度加以直觀處理，平面向量角度加以轉化，坐標角度加以運算等，從而解決相應的問題.

2 問題破解

思維視角一：平面幾何思維.

解法1：(平面幾何法)如圖1所示，取AB的中點D，在AC上取一點E，使AC=3AE，連接OD，OE，DE，其中OA交DE于點F，則AD=1，AE=1，OD⊥AB.而∠BAC=60°，則知△ADE為正三角形，從而DE=1，∠ODE=30°.

圖1

在△ABC中，由余弦定理，可得

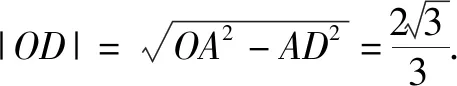
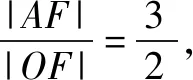
點評：根據平面向量“形”的特征，以及平面向量的線性關系式，通過三角形圖形的直觀，結合余弦定理與正弦定理的應用，利用三角形面積的轉化確定對應邊長之間的比值，從而把平面向量的線性關系式轉化為以A為起點的三個共線的向量之間的線性關系式問題，利用共線向量的性質建立關系式來求解.

思維視角二：平面向量思維.

圖2

結合余弦定理的向量式，有

所以，4x+3y=2.

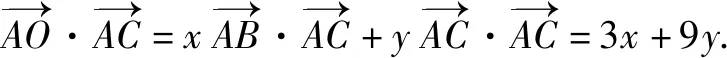
結合余弦定理的向量式，有

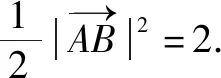
所以，4x+3y=2.

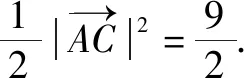
圖3

在△ABC中，由余弦定理，可……