“放縮構造”促進高中數學高階思維能力提升

?江蘇省如東高級中學

洪 兵

新一輪高考改革已逐步邁入了推進階段，加快新課程改革進程，促進新教材的有效使用，發展學生的高階思維，都是數學教學的重要目標，也是培養學生數學核心素養的重要任務與有力抓手.放縮構造在解題時能力要求較高，若能熟練掌握，必定對學生數學學科核心素養的培養以及高中數學高階思維能力的提升有較大益處.

1 高中數學高階思維界定及表現特征

何謂高階思維?美國教育家布魯姆 (B.S.Bloom)和加涅等對學習理論進行了高階思維的劃分，將認知領域的教育目標分成識記、理解、應用、分析、評價和創造六個類別.其中分析、評價和創造，通常被稱為“高階思維”,它包括問題解決、推理與決策、批判性思維、創新性思維和反思性思維等五個維度，體現思維的高階.

高中生在數學學習中培養了較強的實踐能力、創新精神，具備高中數學高階思維，其特征表現為善于發現問題的特殊性.如發現問題的隱含條件等，說明學生養成了求異思維；若能多角度思考分析問題 ，說明學生具備了創造思維；若能靈活妙用數學思想方法，說明學生具有了開放思維.

2 及時發現問題特殊性，培養求異思維

2.1 利用收斂原理，夾逼放縮

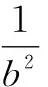
2.2 利用分式形式，極限放縮

問題2已知關于x的不等式a[x-ln(x+1)]≤ex-x-1在x≥0時恒成立，求實數a的取值范圍.

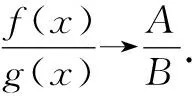
解析：當x=0時，a∈R，則主要研究當x>0時實數a的取值范圍.

由x-1≥lnx恒成立可知x≥ln(x+1)，所以x>0時，x-ln(x+1)>0.

綜上可知，實數a的取值范圍是a≤1.

3 多角度思考分析問題 ，培養創造思維

3.1 利用分層轉化，易元放縮

解題思路：利用分割法求四邊形ABCD的面積，在兩個三角形中分別使用余弦定理，多角度分析簡單的幾何問題 ，再將所有的關系式互相聯系，培養學生的創造性思維.

另外，已知二元變量x,y滿足函數t(x,y)，先以變量x為主元，令f(x)=t(x,y)，求得f(x)=t(x,y)的最值φ(y)，再以變量y為主元，求得φ(y)的最大值.利用分層處理，易元放縮，培養學生創造思維，提升數學高階思維能力.

解析：連接BD，將平面四邊形ABCD分割成兩三角形.

在△BCD中，有BD2=CB2+CD2-2CB·CDcosC=22+22-2×2×2cosC=8-8cosC.

在△ABD中，有BD2=AB2+AD2-2AB·ADcosA=12+42-2×1×4cosA=17-8cosA.

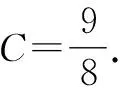
在三角形中，易知A,C∈(0,π)，sinA>0，sinC>0.

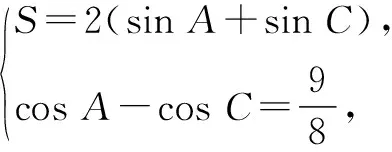
3.2 利用同構特征，單調放縮

問題4(2020年高考山東卷第22題改編)已知函數f(x)=aex-1-lnx+lna,若f(x)≥1，求實數a的取值范圍.(答案：[1,+∞).)

解題思路：對于復雜的不等式構造出同構不等式，形如f[g(x)]≥f[h(x)]，由函數y=f(x)的單調性，化簡得g(x)與h(x)的不等關系式，再研究參數的取值范圍.利用整體思想，分層次轉化，達到降維的目的.

解析：f(x)=aex-1-lnx+lna=elna+x-1-lnx+lna≥1等價于

elna+x-1+lna+x-1≥lnx+x=elnx+lnx

①

令g(x)=ex+x,①式等價于

g(lna+x-1)≥g(lnx).

顯然g(x)為單調增函數，所以lna+x-1≥lnx，即lna≥lnx-x+1.

所以，在區間(0,1)上，h′(x)>0,h(x)單調遞增；在(1,+∞)上，h′(x)<0,h(x)單調遞減.

所以，h(x)的最大值為h(1)=0,即lna≥0，解得a≥1.

故填答案：[1,+∞).

4 靈活妙用數學思想方法，培養開放思維

4.1 利用曲線相切，傳遞放縮

解題思路：此類問題的思考角度很多，從不等式的角度尋求思路繁瑣.讓學生認真觀察提出不同見解，根據圖形的特征，靈活妙用數學思想方法，突破思維瓶頸，培養學生開放思維，從而提升數學高階思維能力.

由函數y=f(x)與y=g(x)圖象在點(x0,f(x0))處相切，且f(x)≥g(x0)≥g(x),f(x0)=g(x0) , 則f(x)的最小值為f(x0)=g(x0).

當a>1時，

=1-cosx≥0(x=0取等號).

4.2 利用數形結合，幾何放縮

5 結束語

“放縮構造”整合高中數學知識，對應變能力有較高的要求.數學時應抓住題目的特點，根據不同題目的類型，采用恰到好處的放縮方法，特別在不等式恒成立有解求參、不等式放縮證明、函數最值與超越函數間的關系等問題的研究，體現非常充分；教學時應精心設置問題，總結基本的放縮方法和放縮調整手段.鼓勵學生積極探究，啟發深度思考，激發深度學習.

可見，“放縮構造”可以作為高中階段提升思維和邏輯推理能力、分析問題和解決問題的能力的支點，探究解決問題的方法和途徑.“放縮構造”是積累思維經驗的過程，提升學生數學高階思維能力，從而達到培養學生數學學科核心素養的目的.