巧借拋物線定義 妙解數學綜合題

河北省唐山市第一中學

李桂蘭

定義是解決相關問題的理論基礎和靈魂所在，解題時要善于回歸定義和應用定義.拋物線的定義反映了拋物線的本質特征，揭示了曲線存在的幾何性質與規律，恰當借助拋物線的定義，能夠有效實現拋物線上的點到焦點的距離與它到準線的距離之間的合理轉化.一方面可以將拋物線上的點到準線的距離轉化為該點到焦點的距離，建構“兩點距離”的直觀問題；另一方面可以將拋物線上的點到焦點的距離轉化為該點到準線的距離，建構“點線距離”的直觀問題.根據不同的問題情境，有效轉化，合理破解，能起到事半功倍的效果.

1 長度問題

例1[2021屆貴州省西南名校聯盟(金太陽)高三下學期(3月)開學考理科數學試卷·16]已知拋物線C：y2=6x的焦點為F，準線為l0，過F且斜率為1的直線l與C交于A，B兩點(A在B的上方)，過點A作AP⊥l0，垂足為P，點G為∠PAB的角平分線與l0的交點，則|FG|=______.

分析：借助幾何視角切入，實現平面解析幾何問題幾何化，通過拋物線的定義以及幾何圖形的直觀，找出相應的全等三角形，利用兩直線垂直的斜率關系確定對應的直線方程，結合交點坐標的確定，并利用兩點間的距離公式求解即可.

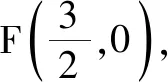
根據拋物線的定義，有|AP|=|AF|，又∠PAG=∠FAG，所以△PAG≌△FAG.

點評：巧妙借助拋物線的定義，實現兩線段之間距離的等價轉化，這也是拋物線的定義的最基礎的應用之一.破解此題的基本思路有兩種.①從代數視角出發，設線，設點，聯立方程是常規方法；②從幾何視角出發……