導數中不等式問題常見的證明策略

浙江省諸暨中學暨陽分校

沈寶偉

導數中的不等式證明問題經常出現在高中數學解答題中，常常和函數零點、極值等不同知識點結合考查.導數中的不等式證明問題雖然難度較大，但有關解答問題的思路多種多樣.針對不同的問題，采取不同的解題方法，往往能達到事半功倍的效果.本文中將對3道不同例題進行分析，分別闡述證明導數不等式問題的四種不同解題策略.

1 構造函數法

利用構造函數方法證明導數不等式問題，主要是通過對不等式的變形加以構造函數.如，要證f(x)≤g(x)可以轉化為證明F(x)=f(x)-g(x)≤0.進一步對F(x)在對應區間的單調性和極值進行探究，得到F(x)值域的上界，就能證明原不等式成立.

例1已知函數f(x)=aex+2x-1，其中e是自然對數的底數.求證：對任意的a≥1，當x>0時，都有f(x)≥x(x+ae).

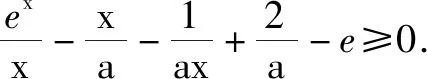
綜上所述，對任意a≥1，都有f(x)≥x(x+ae)成立.

思考：上述問題求解中，把證明不等式問題轉化為函數極值求解問題，正是借助了構造函數的方法和思路，具有一定的借鑒意義.應該注意的是，解題過程中，aex-x-1≥ex-x-1運用了放縮思想，使問題求解更直接，值得反復推敲并學習.

2 切線放縮法

所謂切線放縮法，主要指利用函數在指定點附近對應的切線在函數圖象的一側的特點，進行去指數化、去對數化，從而對導數中不等式證明問題進行求解.如求證xlnx≥asinx-1時，由于f(x)=xlnx在x=1處切線方程為y=x-1，且xlnx≥x-1，對此所證不等式可以轉化為x-1≥asinx-1，進而求證即可.運用函數切線特點放縮不等式，能使解題思路變得更加清晰直觀.

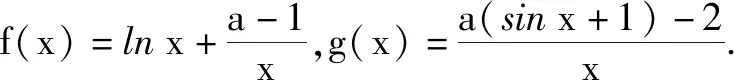
分析：通過簡化首先得到xlnx>asinx-1，此時對……