探究習題教學策略 提升數學核心素養
——由教材的一道課后習題引發的思考

何佩姬

(廣東省清遠市佛岡縣佛岡中學,511600)

《普通高中數學課程標準》(2017年版)(以下稱“課程標準”)指出:“高中數學教學以發展學生數學學科核心素養為導向,啟發學生思考,引導學生把握數學內容的本質,提倡獨立思考、自主學習、合作交流等多種學習方式,激發學習數學的興趣,養成良好的學習習慣,促進學生實踐能力和創新意識的發展”[1].數學習題是教材的重要組成部分,是數學教學過程中組織學生學習、實踐活動的一種重要形式[2].因此，如何在解題教學中培育學生的數學核心素養，值得積極探究.

本文以新教材人教A版普通高中教科書必修第一冊(簡稱“教材”)的一道課后習題為例,探究數學習題教學策略.

一、教學過程

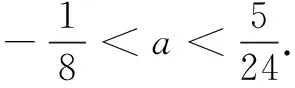
從學生完成的情況來看,基本都能得出“此題是不正確的”的結論,并找出一些不正確的理由.此題看起來簡單,但易錯,絕大部分的同學考慮不全面,出現“漏解”.針對此情況,筆者讓學生投影解答過程的同時分享解題思路.

首先，利用隨機抽檢法抽到學生L.該同學說出了此題的錯因，但只考慮了函數f(x)=24ax2+4x-1在區間(-1,1)存在零點,而沒有考慮到函數在區間(-1,1)恰有一個零點,說明該同學對函數的零點存在性定理理解得不夠透徹.

接著,請學生T到講臺來講評其做法.其解答大致如下:函數f(x)=24ax2+4x-1在區間(-1,1)恰有一個零點,即函數圖象在(-1,1)與x軸有唯一交點,即方程24ax2+4x-1=0在(-1,1)恰有一個解.

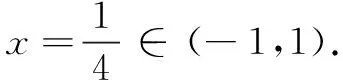
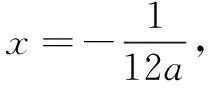
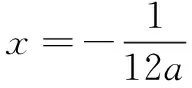
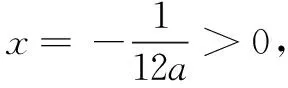
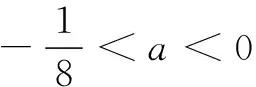
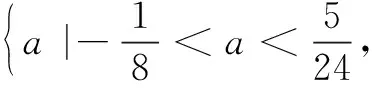
T剛講完他的解題思路和過程，學生Y說“老師,這道題目還可以再簡化,把a>0和a<0兩種情況統一為一種情況.”,其解答過程如下:

(2)當a≠0時,Δ=42-4×24a×(-1)=16+96a.

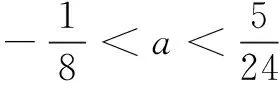
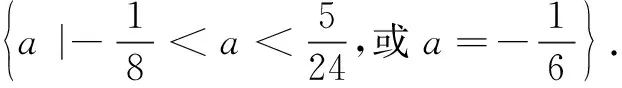
在肯……