電子方艙熱仿真的等效模型與參數優化
袁偉琪,葉 銳
(中國電子科技集團公司第三十八研究所,安徽 合肥 230088)
0 引言
作為戰場上重要的作戰節點,電子方艙經常暴露于嚴苛的環境之下,方艙需要耐受夏季55℃的高溫和太陽輻照;冬季里-40℃的低溫,這些環境因素使得方艙的保溫性能要求很高,電子方艙的熱性能設計對其正常工作至關重要。
方艙設計過程中需要同時考慮傳熱系數、電磁兼容性和結構強度等多種性能,其設計工作復雜。隨著計算機技術發展,熱仿真技術在電子方艙的環控設計中扮演了越來越重要的作用:黃健借助CFD軟件模擬了車載醫療方艙風道,驗證了數值方法的可靠性[1];張夢龍等運用FLUENT軟件分析空調不同送風參數對于方艙降溫效果的影響,并提出了制冷系統冷氣通路的改進措施[2];陳文博等利用有限元輔助設計方法提升方艙升溫過程設計的效率和精度,實驗結果表明仿真計算結果誤差在6%~22%,處于工程仿真誤差范圍之內[3]。
前人工作表明仿真分析方法輔助方艙設計的可行性和高效性。但方艙仿真中存在尺寸跨度大的問題,這會加大方艙的網格量,在穩態計算時尚可接受,一旦需要對方艙進行瞬時計算,模擬升降溫過程,計算量將會非常大,耗時長,降低設計效率。針對方艙熱仿真特點,使用了分步計算的方法對方艙進行模擬:先通過詳細建模計算出方艙艙壁的等效導熱率,再將方艙整體建模,利用前述等效參數減少整體仿真的計算量,達到提升計算效率的目的。同時針對方艙進行詳細建模,對比了不同尺度下兩種計算方式的計算量及仿真結果。
1 模型介紹
1.1 方艙模型
軍用方艙是目前電子通信系統的主要載體之一,一般運用保溫艙壁、空調及加熱器等措施控制艙內環境參數。其中,方艙艙壁的保溫性能決定了艙體的冷熱負荷,對方艙環境參數和耗電量有顯著影響。方艙傳熱系數是衡量艙壁保溫性能的重要指標,針對方艙傳熱系數開展了一系列仿真工作,典型的方艙艙壁采用聚氨酯發泡中間加金屬骨架的大板式形式,如圖1所示,由隔熱層、方艙骨架、內外蒙皮以及斷熱橋組成。
1.2 仿真模型
1.2.1 一般模型
一般熱仿真中針對整個方艙(去除不影響傳熱的特征)進行建模,將所有特征一一建立模型并賦值,如圖2所示。
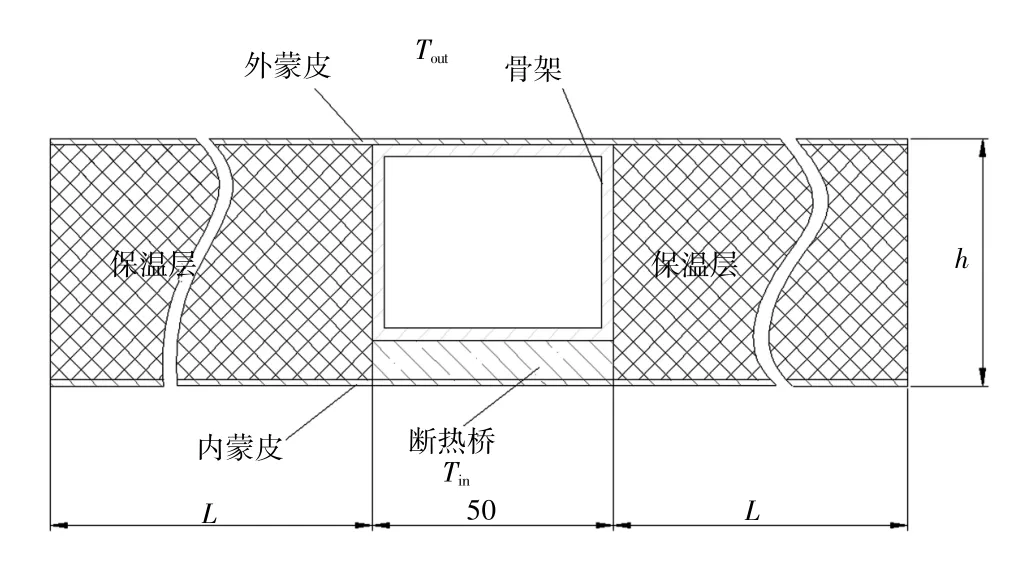
圖1 方艙艙壁模型
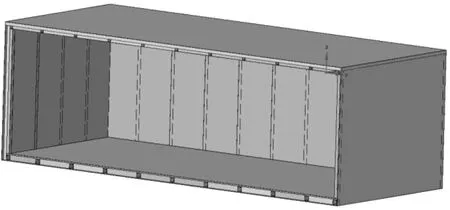
圖2 電子方艙一般模型
根據國標要求,仿真計算時在方艙內部放置熱源,通過調整熱源散熱量使內部空氣溫度穩定為20℃,外部氣流速度不大于2 m/s,環境溫度-35℃[5],通過式(1)計算方艙傳熱系數。

式中,h為方艙傳熱系數,單位W/(m2K);△T為艙內外溫差,℃;A為方艙表面積,m2。
艙壁上特征較多,小尺寸的特征如骨架、蒙皮等長寬尺寸較大,而厚度小,且放置方向不同,仿真軟件劃分網格時會以薄壁厚度為最小尺度為基準,這會帶來大量非必要的網格,使得模型網格量大幅度增加,提高計算量。
1.2.2 等效模型
為了減少仿真計算量,根據幾何模型簡化原則,在方艙仿真時分成兩步進行:將艙壁作為一個整體看待,先計算出單位長度的模塊艙壁的熱物性;建立簡化方艙模型,利用上一步求得的熱物性為艙體賦值,從而減少計算量。詳細過程如下:
第一步,艙體熱物性計算:與一般模型類似,針對單位長度(主要取決于骨架間距)的艙體詳細建模,利用仿真軟件計算不同方向傳熱系數,進而計算出各個方向的熱導率(式2),模型如圖3所示。
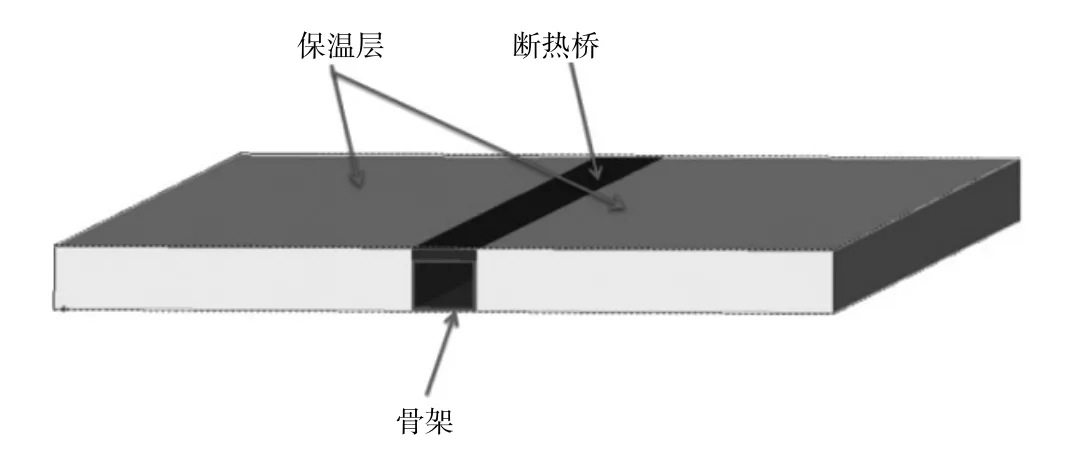
圖3 等效模型步驟1示意圖

式中Q為通過艙壁的總熱量,W;d為艙壁厚度,m;A為艙壁面積,m2。
第二步,建立方艙模型,其中艙壁為實心塊狀模型,如圖4所示,并將等效參數賦值給艙壁。
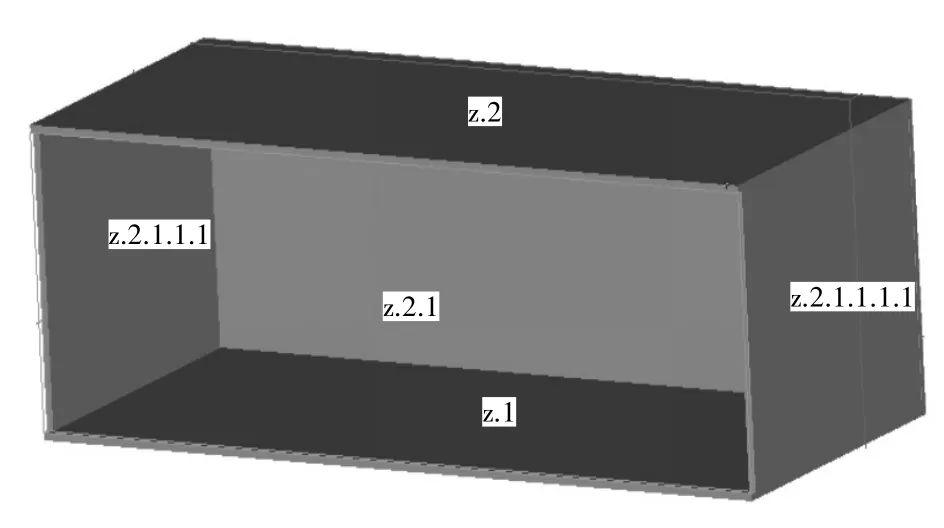
圖4 等效模型步驟2示意圖
相比于一般模型,等效模型只有在第一步中針對單位長度的艙壁完整結構建立模型,減少了建模工作量同時可以大幅度較少仿真網格量,又不影響仿真準確度。
2 仿真結果
本節中利用第二節的方艙模型,利用軟件分別進行仿真。
2.1 驗證等效模型準確性
參考真實的方艙結構建立模型,驗證等效模型的準確性。常見方艙的傳熱系數約為1.5 W/m2·K,典型艙壁材料見表1。

表1 方艙材料參數
參照GJB 2093A-2012 7.6節保溫性試驗方法,仿真分析時將外蒙皮壁面溫度設置為-35℃,內蒙皮壁面溫度設置為20℃,通過計算漏熱量,評估其散熱性能。結果見表2、圖5。

表2 等效模型第一步結果

圖5 縱切面溫度分布圖
針對方艙及內部熱源建模,多次迭代使內部溫度為20℃(環境-35℃,風速最大約1.6 m/s),此時熱源制冷量約為5000 W,利用公式(1)計算得方艙傳熱系數為1.46 W/(m2·K),結果見表3、圖6。

表3 等效模型第二步結果
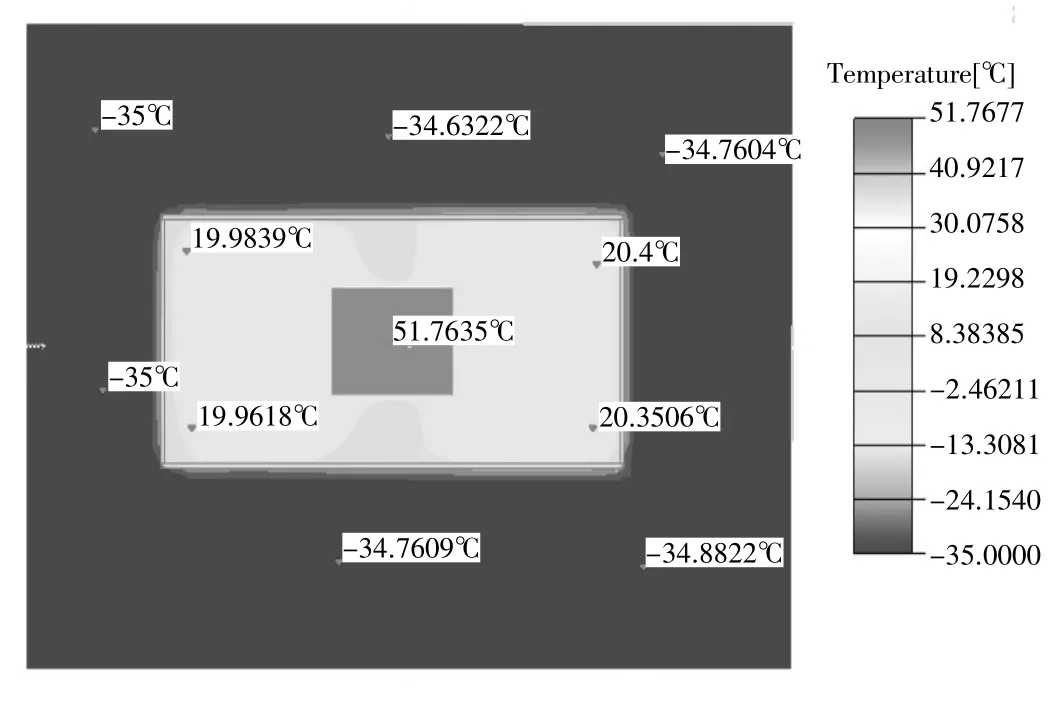
圖6 橫切面溫度云圖
結果表明,仿真結果與實測結果差距不超過3%,仿真結果準確可靠。
2.2 不同模型仿真結果對比
以壁厚150 mm,骨架50 mm*50 mm,骨架間距600 mm的方艙為例,對比兩種仿真模型的結果,如下所示:
(1)等效模型
第一步:計算艙體導熱率,結果見表4和圖7。

表4 等效模型第一步結果
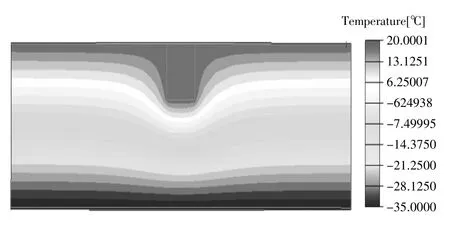
圖7 縱切面溫度云圖
第二步,計算方艙傳熱系數,結果見表5和圖8。

表5 等效模型第二步結果
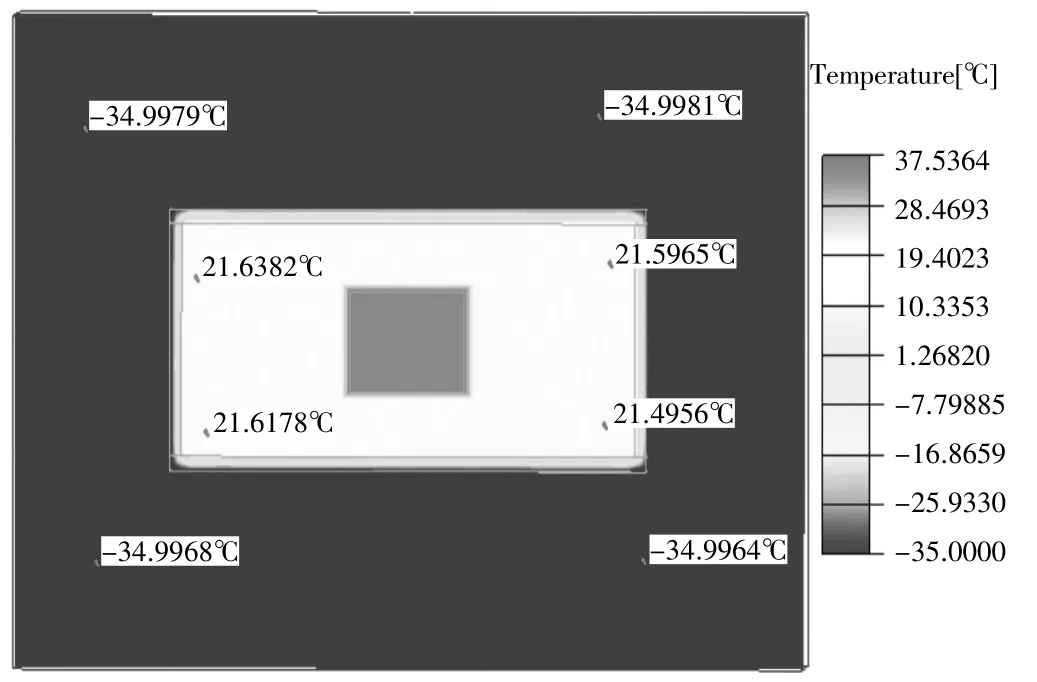
圖8 橫切面溫度云圖
(2)一般模型
針對方艙整體建模,為了兼顧仿真精確度及效率,設置每個邊上有兩個節點,模型仿真,結果見表6和圖9。

表6 一般模型結果
對比2種模型結果可其傳熱系數相差約6%,仿真結果較為接近;一般模型的網格數比等效模型高了一個數量級,等效模型可以有效減小仿真計算量,加快仿真速度和設計過程。
在仿真中發現,參數調整時不需要對第二步中的整體模型做過多修改。特別是調整骨架間距,在一般模型中需要改變每根骨架,而等效模型只需要調整模型第一步中的保溫層長度,工作量精簡許多。
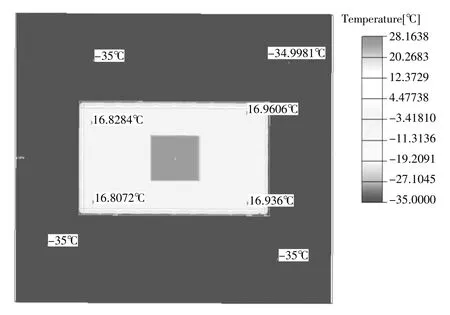
圖9 橫切面溫度云圖
2.3 模型應用與實驗驗證
采用等效模型進行仿真,結合工程需要,方艙設計參數見表7。

表7 方艙結構設計參數
經等效模型計算,方艙傳熱系數仿真約為0.41 W/(m2·K)。以該參數設計某冷藏方艙,通過實驗測得方艙傳熱系數約為0.38 W/(m2·K),等效模型仿真結果偏離約8%。
3 結語
軍用電子方艙由于其提供良好的電子器件及人員工作環境而廣被使用,在其設計過程中,熱仿真是保證性能的重要環節。在保證仿真精度的前提下,提出了一種網格和計算量更小的模型,并對其進行驗證。結果表明該模型有著較高的準確性,且相比于完整建模的一般模型,網格數大大減少,且在參數修改時更加方便,可以極大提高設計效率。

