七軸澆鑄機器人運動學建模及仿真
王占光,王 健,袁明新,2,江亞峰
(1.江蘇科技大學蘇州理工學院,江蘇 張家港 215600;2.張家港江蘇科技大學產業技術研究院,江蘇 張家港 215600)
0 引言
我國是鑄造大國,鑄造產量位居世界第一。鑄造行業長期以高消耗、高污染、低產出、低收益的特點發展,這種粗放式的發展模式越來越不適應產業發展需求[1]。隨著鑄造裝備的技術改革創新,工業機器人在鑄造行業得到了廣泛應用,促進鑄造行業向自動化、智能化的方向發展[2]。澆鑄作業區工作環境惡劣,高溫、粉塵、噪聲污染嚴重[3],影響作業人員的工作效率。目前,澆鑄自動化生產單元一般將設備按照扇形布置,一位作業人員為1~2臺鑄造機舀入鋁液,澆包加上產品重量可達30 kg,作業人員被熔化爐與鑄造機圍繞,周圍環境溫度達40℃以上,這種高溫高強度的澆鑄讓作業人員體能的迅速消耗[4],造成澆鑄質量的不穩定。工業機器人運動精度高,工作穩定性好,可以連續作業,應用機器人進行澆鑄能夠降低單件產品成本。工業機器人代替人工是澆鑄行業發展的趨勢,具有節省勞動力成本、提高產品質量和穩定性、提高生產效率等優點。
澆鑄自動化生產單元大多選用六軸關節工業機器人,在實際應用中,直接利用第六軸進行澆鑄作業存在的弊端有:(1)澆鑄動作不穩定,影響產品質量的穩定性;(2)機器人在澆鑄過程要多次調整姿態,影響生產節拍;(3)第六軸直接和澆包相連,容易造成機器人本體故障,影響機器人使用壽命。經過技術上的改革創新,在澆鑄機器人基礎上增加第七軸,利用伺服電機驅動鏈輪或者齒輪傳動,獨立完成澆包澆鑄動作,形成七關節澆鑄機器人。本研究在分析七軸澆鑄機器人應用特點的基礎上,建立了機器人的運動學模型,建立正運動方程并給出求解過程,通過仿真驗證其正確性。
1 機器人結構及運動學模型
以日本FANUC公司的R-2000iC/165F工業機器人為基礎,該機器人具有6個旋轉關節,重復定位精度±0.2 mm,末端最大負載165 kg。FANUC澆鑄版機器人表面及空腔內均涂有特殊防高溫剝落涂層,外露螺栓和墊片采用防銹材質,馬達電機等區域采用了罩殼對其保護,增強了在惡劣環境中的使用壽命。在第六軸上增加獨立傳動的附加軸,將機器人本體與高溫的取液口相隔離,對機器人本體具有保護作用。附加軸由伺服電機、減速器、傳動桿、傳動桿箱、蝸輪蝸桿、控制裝置、澆包等機構組成[5],傳動桿箱上端有連接法蘭,與機器人第六軸相連,使得傳動桿箱與第六軸軸向方向垂直。通過控制伺服電機調整澆包的轉動速度和角度,從而實現澆鑄過程的控制。在SOLIDWORKS中建立七軸澆鑄機器人三維模型如圖1所示。

圖1 七軸澆鑄機器人三維模型
澆鑄工業機器人的七個關節都是旋轉自由度,通過串聯的方式連接。其中第1軸、第2軸和第3軸用來確定空間位置(定位功能),第4軸、第5軸和第6軸用來調整空間姿態(定向功能),附加軸用來控制澆包的動作。機器人在執行自動化澆鑄任務中,各軸是不斷運動的,每一根連桿的運動會對該連桿的相鄰連桿的運動產生影響。為了準確描述機器人的運動,兩位科學家Denavit與Hartenberg提出了D-H參數建模法,該方法是目前應用廣泛的一種機器人建模方法[6]。根據標準D-H法,將機器人看作連桿結構,在每一個連桿建立一個坐標系,該坐標系與對應的連桿是相對靜止的。澆鑄機器人主要是末端澆包的澆鑄動作,因此需要對澆包的位置和姿態進行描述,所以將坐標系的原點建立在關節連桿末端。
建立標準D-H連桿坐標系如圖2所示,建立原則如下:(1)Zi軸沿著第i+1關節的軸向方向;(2)坐標系原點為Zi-1與Zi軸的交點或兩軸公垂線與Zi軸的交點;(3)Xi軸沿Zi-1與Zi軸的公垂線方向,由第i關節軸指向第i+1關節軸;(4)Yi軸方向根據Xi軸和Zi軸按照右手定則確定。

圖2 七軸澆鑄機器人連桿坐標系
根據設定的連桿坐標系,相應的連桿參數定義如下:(1)關節角θi:繞Zi軸使Xi-1軸旋轉到Xi軸同向且共線的角度,繞Zi軸正向旋轉為正;(2)關節偏距di:沿Zi-1軸從Xi-1到Xi軸的距離,沿Zi-1軸正方向為正;(3)連桿長度ai為沿Xi軸使Zi-1軸移動到Zi軸的公垂線距離,沿Xi軸正方向為正;(4)連桿轉角αi:繞Xi軸使Zi-1軸與Zi軸同向且共線的角度,繞Zi軸正向旋轉為正[7]。由于工業機器人零點位置為圖1所示姿態,所以θ2的初始值為90°,θ6的初始值為180°,其他關節的初始值均為零。根據D-H方法,得到連桿關節參數見表1。
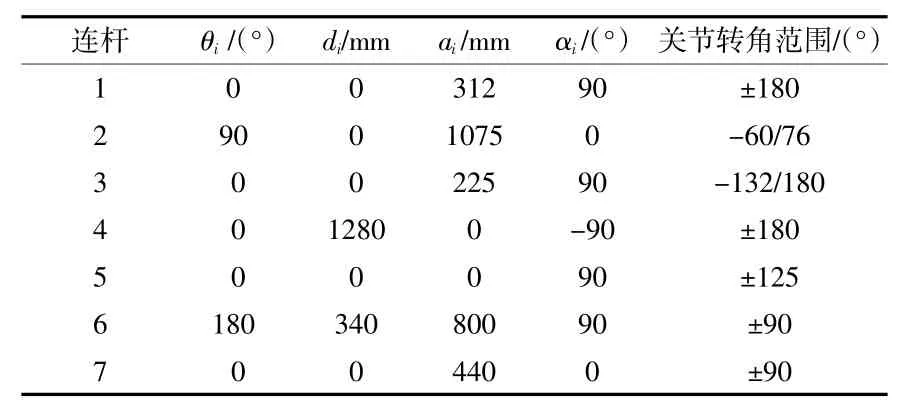
表1 機器人D-H參數表
2 機器人正運動學求解
建立的機器人運動模型中,相鄰的兩個坐標系可以通過一系列的平移、旋轉等變換得到[8]。根據連桿的運動關系,坐標系Oi-1轉換到坐標系Oi過程如下:(1)繞Zi-1軸旋轉θi角度;(2)沿Zi-1軸移動di距離;(3)沿Xi軸移動ai距離;(4)繞Xi-1軸移動αi角度。由θi、di、ai、αi這4個參數,通過4次齊次變換矩陣描述相鄰兩個坐標轉換過程表述如下:

將表1中的D-H參數代入公式(1)得到各連桿的齊次變換矩陣如下:


對于7關節的工業機器人,將各連桿的變換矩陣相乘,得到

式(9)為澆鑄機器人正運動學模型,各項的表達式沒有詳細展開。其中,代表末端坐標系O7相對于基坐標系O0的姿態,代表末端坐標系O7的位置。在澆鑄機器人每個關節的關節坐標已知的條件下,我們可以求得末端澆包的關節坐標,這樣澆包的位置和姿態就可以描述了。
3 機器人正運動學仿真
為了驗證正運動學算法的正確性,結合Matlab Toolbox工具箱進行實例仿真,進行本研究的機器人的位姿驗證。分別在給定初始角度和指定角度條件下,對比運動學方程計算結果和仿真結果,流程如下:
(1)初始角度驗證
原點位置各關節的關節坐標為零,給出機器人關節矩陣θ=[0 0 0 0 0 0 0],帶入公式(9)得到:

得到初始位置的末端坐標為(1932,0,60),利用Matlab工具箱的Link函數將建立的各連桿串聯起來,得到機器人初始位置的仿真模型如圖3所示。由圖3可知,初始角度仿真方法得到的正解結果和解析法求得的結果是一致的。

圖3 初始角度模型仿真結果
(2)指定角度驗證
機器人各關節角度任意指定一個角度值:θ1=90,θ2=-30,θ3=30,θ4=15,θ5=30,θ6=-15,θ7=-30,將以上角度轉化為弧度,帶入公式(9)得到

得到指定角度的末端坐標為(55.0869,2803.8270,180.5131),利用Matlab仿真得到機器人初始位置的模型如圖4所示。由圖4可知,指定角度仿真方法得到的正解結果和解析法求得的結果是一致的。
綜上,機器人的正運動學模型的計算結果和Matlab仿真結果一致,證明了模型建立的正確性。

圖4 指定角度模型仿真結果
4 結束語
根據澆鑄機器人的應用特點,分析了七軸澆鑄機器人的結構,建立了機器人的運動學模型,介紹了正運動學求解的過程,并且利用Matlab仿真驗證了模型的正確性,為優化機器人路徑及提高澆鑄自動化效率提供了設計依據。

