借助例題，提升學(xué)生解題能力

張軍

【摘 要】 在初中數(shù)學(xué)課堂，例題具有難度系數(shù)小、內(nèi)容覆蓋全的特點(diǎn).借助例題訓(xùn)練學(xué)生的數(shù)學(xué)思維，不僅能夠幫助學(xué)生快速理解相關(guān)知識(shí)點(diǎn)，也能提升學(xué)生解題能力，吃透數(shù)學(xué)原理、定義、性質(zhì)等相關(guān)概念，將例題演示作為一種教學(xué)策略，可以有效推進(jìn)數(shù)學(xué)課堂的高效生成.

【關(guān)鍵詞】 初中數(shù)學(xué);例題;教學(xué)策略

例題是指導(dǎo)學(xué)生學(xué)習(xí)并應(yīng)用原理知識(shí)的重要方式，也是數(shù)學(xué)課堂中必然引用的教學(xué)方法.在平時(shí)教學(xué)中，存在學(xué)生聽(tīng)例題能聽(tīng)懂，但依然無(wú)法獨(dú)立解題的現(xiàn)象.針對(duì)學(xué)生的問(wèn)題，提出使用例題多向用途，以解題問(wèn)題著手，發(fā)展學(xué)生的邏輯思維，將例題進(jìn)行變式演練，要求學(xué)生在學(xué)習(xí)過(guò)程中習(xí)慣反思，發(fā)現(xiàn)潛在規(guī)律，熟悉題目規(guī)則的基礎(chǔ)上，可以自主改編題目，構(gòu)建自己的知識(shí)體系，生成高效數(shù)學(xué)課堂.

1 設(shè)置梯級(jí)問(wèn)題，發(fā)展邏輯思維

教師利用例題進(jìn)行課程講述時(shí)，一般使用課本所述例題，但每個(gè)學(xué)生的理解能力不同，對(duì)例題中所包含的知識(shí)要點(diǎn)掌握情況也不盡相同.此時(shí)教師可以在例題講解過(guò)程中設(shè)置階梯問(wèn)題，引導(dǎo)學(xué)生逐步思考，從而激發(fā)學(xué)生學(xué)習(xí)興趣，適應(yīng)每個(gè)學(xué)生的不同學(xué)習(xí)要求.同時(shí)，階梯問(wèn)題的設(shè)計(jì)方法，為基礎(chǔ)弱的同學(xué)提供了思考空間和進(jìn)步方向.學(xué)生完成了相應(yīng)的問(wèn)題挑戰(zhàn)，發(fā)展了邏輯思維，提高了課堂效率，

例如 點(diǎn)（-l，-5）位于一次函數(shù)y=kx+b的圖像上，該一次函數(shù)與正比例函數(shù)y=0. 5T有一個(gè)交點(diǎn)（2，a），求：

（1）a的值是多少？

（2）k和b的值分別是多少？

針對(duì)（1）中求解，點(diǎn)（2，a）是兩個(gè)圖形的交點(diǎn)，只需要帶入兩個(gè)函數(shù)中的一個(gè)即可計(jì)算結(jié)果.一次函數(shù)為未知函數(shù)，所以帶人正比例函數(shù)即可計(jì)算結(jié)果，a=0.5×2=1.第一問(wèn)最簡(jiǎn)單，學(xué)生都可以完成計(jì)算.

針對(duì)（2）中求解，k和b都是一次函數(shù)的未知項(xiàng)，按照要求，求解兩個(gè)未知數(shù)，需要用兩個(gè)聯(lián)立的方程組，要求方程組中除k和b外都是已知項(xiàng)，那么意味著必須存在兩組（x，y），題目中已知一組（-1，-5），繼續(xù)尋找一組.部分學(xué)生發(fā)現(xiàn)題目后續(xù)條件中，一次函數(shù)和正比例函數(shù)存在交點(diǎn)（2，a），在（1）中求得a為1，那么意味著交點(diǎn)也是一次函數(shù)的點(diǎn)，所以第二組為（2，1），聯(lián)立即可解題.

因此，在數(shù)學(xué)例題講解中，使用梯級(jí)問(wèn)題的方式，給學(xué)生提供了思維方向，在特點(diǎn)要求和條件下，訓(xùn)練學(xué)生的邏輯思維能力，快速得到結(jié)果，例題的講解為基礎(chǔ)較弱的學(xué)生提供了學(xué)習(xí)方向，形成你追我趕的動(dòng)力課堂，提高了課堂效率.

2 辨析出現(xiàn)的錯(cuò)誤，形成反思習(xí)慣

在日常教學(xué)中，數(shù)學(xué)教師引用例題進(jìn)行課題引入或者知識(shí)講解，通過(guò)正向思維引導(dǎo)學(xué)生學(xué)會(huì)學(xué)習(xí)數(shù)學(xué)，但學(xué)生在實(shí)際做題過(guò)程中依然存在錯(cuò)誤，針對(duì)該問(wèn)題，筆者提出錯(cuò)誤例題講解模式，使用錯(cuò)誤作為先導(dǎo)，要求學(xué)生辨析出現(xiàn)的錯(cuò)誤，從錯(cuò)誤的解法或者思維中找到關(guān)鍵問(wèn)題，從而形成反思習(xí)慣，有效防止日常做題中的慣性錯(cuò)誤思維.

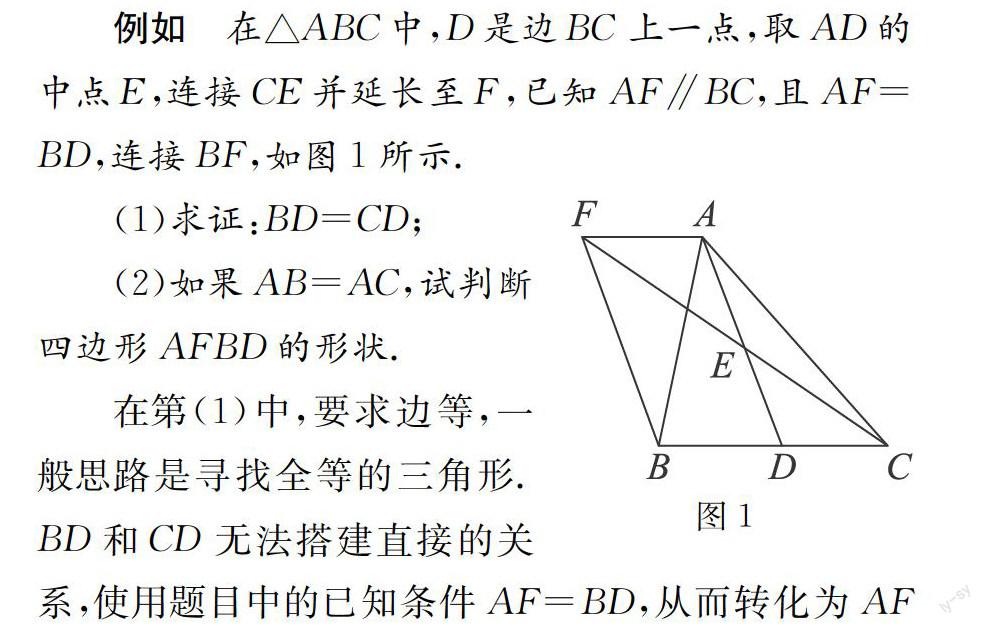
例如 在△ABC中，D是邊BC上一點(diǎn)，取AD的中點(diǎn)E，連接CE并延長(zhǎng)至F，已知AF∥BC，且AF=BD，連接BF，如圖1所示.

（1）求證：BD= CD;

（2）如果AB=AC，試判斷四邊形AFBD的形狀.

在第（1）中，要求邊等，一般思路是尋找全等的三角形.BD和CD無(wú)法搭建直接的關(guān)系，使用題目中的已知條件AF=BD，從而轉(zhuǎn)化為AF=CD進(jìn)行驗(yàn)證.平行必然有角等，利用△AFE和△DCE全等即可證明.

在第（2）中，學(xué)生猜測(cè)四邊形AFBD是平行四邊形，有了AF∥BC，只需要AF=BD即可驗(yàn)證，似乎思路是正確的，因?yàn)閷?duì)邊平行且相等就可以證明一個(gè)四邊形是平行四邊形，要求學(xué)生繼續(xù)觀察題目，題目中還有一個(gè)隱含的未知項(xiàng)“AB =AC”并未使用，導(dǎo)致分析不全面，造成結(jié)論錯(cuò)誤，正確的結(jié)論，是首先判定AFBD為平行四邊形，再通過(guò)邊等的關(guān)系，判定線段AD存在的意義，因?yàn)镈點(diǎn)是邊BC的中點(diǎn)，而△ABC是等腰三角形，根據(jù)三線合一的理論，AD也是BC邊上的高，所以存在直角，所以得到四邊形AFBD是矩形.

所以，通過(guò)例題的錯(cuò)誤結(jié)論，培養(yǎng)學(xué)生仔細(xì)觀察認(rèn)真思考的習(xí)慣，通過(guò)試題分析練習(xí)，不僅鍛煉了學(xué)生習(xí)題反思的能力，同時(shí)幫助學(xué)生有效復(fù)習(xí)了三角形、平行四邊形和矩形的相關(guān)定理及性質(zhì)，提升了學(xué)生數(shù)學(xué)認(rèn)知能力.

3 歸納通法，發(fā)現(xiàn)潛在規(guī)律

數(shù)學(xué)作為典型的理科題目，在教學(xué)過(guò)程中指導(dǎo)學(xué)生學(xué)會(huì)歸納總結(jié)，在例題講解中發(fā)現(xiàn)、總結(jié)規(guī)律，才能在眾多的題目要求中，看到其本質(zhì)要求.通過(guò)例題培養(yǎng)學(xué)生歸納通法的思維習(xí)慣，發(fā)現(xiàn)題目之間的潛在規(guī)律，訓(xùn)練了學(xué)生思維的發(fā)散能力，培養(yǎng)學(xué)生“新問(wèn)題”也是“舊知識(shí)”的理念，促進(jìn)初中高效課堂的生成.

例如 題1 a的相反數(shù)是它本身，b的倒數(shù)是它本身，則a一b=_____

在自然數(shù)中，相反數(shù)是本身的只有0，倒數(shù)是本身的存在兩個(gè)數(shù)，分別是1和-1，將二者分別代人上式中，可計(jì)算得結(jié)果分別是-1和1.

題2 平方是本身的數(shù)是____

學(xué)生回答O和1.

題3 a和b的平方的結(jié)果相等，a+2=1，b-2=

a+2=1，可得a=-1，如果b和a的平方相等，那么b的值只能是1或者-1，計(jì)算結(jié)果為-1或者一3.

從上述幾個(gè)題目中可以看出，數(shù)學(xué)可以有多種描述，不管是哪種描述，最終結(jié)果都趨向0，±1.除此之外，數(shù)學(xué)中還有大量的結(jié)果相似的題目是借助了某些數(shù)字的特殊變換或者定理的特殊意義，要求學(xué)生在日常學(xué)習(xí)中注意總結(jié)相關(guān)規(guī)律，掌握知識(shí)，從而脫離題海戰(zhàn)術(shù)，提升數(shù)學(xué)學(xué)習(xí)效率.

4 鼓勵(lì)自主改編，引導(dǎo)自主建構(gòu)

相對(duì)上述幾種例題學(xué)習(xí)方法，自主改編例題要求學(xué)生不僅具有一定的數(shù)學(xué)能力，同時(shí)還具有一定的創(chuàng)新能力，通過(guò)對(duì)課堂例題的改編，激發(fā)學(xué)生的參與意識(shí)和激情，激活創(chuàng)造才能，構(gòu)建了知識(shí)體系，還讓學(xué)生理清了解題思路，掌握了題型規(guī)律，串接了數(shù)學(xué)前后知識(shí)，提高了課堂效率.

例如 在上圖1中，要求學(xué)生增加條件，在上述判斷中，四邊形AFBD是矩形，那么增加什么條件，使得四邊形AFBD成為正方形？學(xué)生開(kāi)始思考正方形特點(diǎn)，特別是相對(duì)長(zhǎng)方形的特點(diǎn)，最典型的特點(diǎn)是正方形所有邊長(zhǎng)都相等，意味著在（2）的基礎(chǔ)上，增加AF=AD即可，還有什么特點(diǎn)呢？學(xué)生繼續(xù)回憶，正方形對(duì)角線長(zhǎng)度相等且相互垂直平分，加入題目中，如何證明？

學(xué)生指出，如果證明結(jié)論是正方形，第（3）問(wèn)為“如果AF=AD，四邊形AFBD是什么形狀？”要求學(xué)生思考，（1）是必然存在的條件，證明可以在后續(xù)解答中直接使用，而（3）是在（2）的基礎(chǔ)上進(jìn)行的問(wèn)答，所以是否應(yīng)該繼續(xù)健全題目？通過(guò)問(wèn)題的規(guī)范指導(dǎo)，學(xué)生不儀復(fù)習(xí)了正方形和長(zhǎng)方形的知識(shí)，同時(shí)對(duì)其相關(guān)性質(zhì)進(jìn)行對(duì)比聯(lián)系學(xué)習(xí)，構(gòu)建了兩個(gè)圖形的知識(shí)體系.

所以，借助例題進(jìn)行初中數(shù)學(xué)課堂講解，引導(dǎo)學(xué)生掌握了基礎(chǔ)知識(shí)，也在一定程度上拓寬了學(xué)生視野，訓(xùn)練了學(xué)生數(shù)學(xué)思維，在題目的不同分析中尋找客觀規(guī)律，從而提升了學(xué)習(xí)效率，也提高了課堂效率.

【課題名稱：初中數(shù)學(xué)教學(xué)中有效融入數(shù)學(xué)發(fā)展史的應(yīng)用研究，課題編號(hào)：JQ[2021]GHB031】

參考文獻(xiàn)：

[1]葛燁.借助例題推促初中數(shù)學(xué)課堂高效生成[J].山西教育（教學(xué)），2019（06）：19-20.

[2]顧紅英，初中數(shù)學(xué)例題的有效教學(xué)方法研究[J].中學(xué)課程輔導(dǎo)（教師教育），2021（14）：87—88.

[3]薛麗雅，關(guān)于初中數(shù)學(xué)例題教學(xué)的幾點(diǎn)思考[J].中學(xué)數(shù)學(xué).2020（02）