在數學實驗中理解“余數”
——《有余數的除法》教學片斷與思考

文|張 彥

《有余數的除法》是蘇教版教材二年級下冊的教學內容。作為這個單元的起始課，本課教學的重點是認識“有余數的除法”，難點是理解“余數要比除數小”。在教學中，教師的目光不能僅僅停留在課時的知識點上，而是要具備知識、方法和過程的結構意識，進行整體架構。對于二年級的學生，對“有余數的除法”的知識建構和意義理解感到比較抽象深奧，基于這樣的學情，怎樣促進學生理性思維發展呢？數學實驗是打開學習的有效方式，讓學生通過動手動腦，“做”中學，在問題啟思下，借助實驗材料，展開操作和交流，從而認識有余數的除法，理解余數和除數之間的關系。

片斷一：在“分蘋果”的數學實驗中完善建構

師：同學們，認識它嗎？（小豬佩奇）

師：小豬佩奇正在果園里摘蘋果。摘了10個蘋果（出示10個蘋果圖），每人分2個，可以分給幾人呢？

生：5人。

師：每人分2個，也就是2個2個分，可以分給5人，正好分完。佩奇把結果記了下來。

師：那10個蘋果，如果每人分3個，結果會怎樣？每人分4個？5個呢？動手分一分、填一填、說一說。

師：我們可以像佩奇那樣，同桌合作，用圓片代替蘋果分一分，把每次分的結果記在表格里。再互相說一說，每次分得的結果怎樣？

交流：老師收到了這些分法，看得懂嗎？你們也是這樣分的嗎？誰來介紹一下？結合圖說一說。

生1：10個蘋果，每人分3個，可以分給3人，還剩1個。

生2：10個蘋果，每人分4個，可以分給2人，還剩2個。

生3：10個蘋果，每人分5個，可以分給2人。

出示《記錄單》：

?

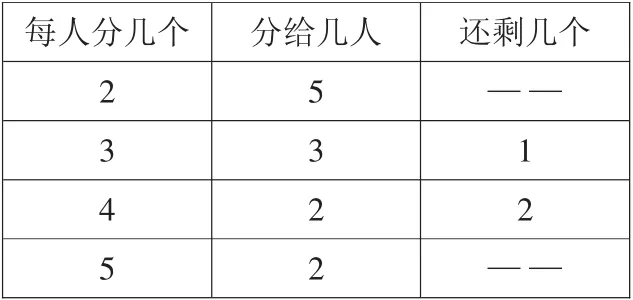
師：把10個蘋果平均分，我們得到了這些結果。仔細觀察，你有什么發現呢？同桌討論。

生：有的正好分完，有的有剩余。

師：（追問）哪些情況是正好分完的？有剩余的呢？

發現：把10個蘋果平均分，會出現兩種情況：正好分完、有剩余。

【思考：數學實驗不是簡單的動手操作，而是促進學生對未知探索、主動思考和發現的一種方式，學生的已有經驗是“10個蘋果，每人分2個，可以分給5人，正好分完”，那每人分3個、4個呢？這就產生了認知沖突，在結果不可知的情況下，教師組織學生用數學實驗的方式去探究發現，體現了實驗設計的必要性與合理性，通過有序地分一分，記錄分的結果，根據過程體驗和數據觀察，較好地感受平均分有兩種情況，“正好分完”和“有剩余”，幫助學生形成更加完整的知識體系架構。】

片斷二：在“除法算式”表征中滲透數形結合思想

師：像這樣正好分完，你會用除法算式表示嗎？

生：10÷2=5（個）。

師：這一種有剩余的情況，也可以寫一個除法算式嗎？

生：10個蘋果，每人分3個，可以分給3人，10÷3=3（人）。

師：還剩1個可以怎樣表示呢？可以在后面點上6個小圓點（……），再在小圓點（……）后寫1（個）。

師：會讀嗎？

生：10除以3等于3人還剩下1個。

師：剩下1個就是“余1個”。

師：這個算式表示什么意思？誰能完整地說一說？

生：10個蘋果，每人分3個，可以分給3人，還剩1個。

師：兩個“3”，意思相同嗎？分別表示什么？1呢？

介紹：1表示剩下的個數，不夠再分，在除法中，它就叫“余數”。這就是有余數的除法。

師：今天這節課我們就來認識《有余數的除法》（揭示課題）。

師：10個蘋果，每人分4個，也可以用有余數的除法算式來表示嗎？

生：10÷4=2（人）……2（個）。

師：兩個2表示的意思相同嗎？

生：商2表示可以分給2人，余數2表示剩下2個蘋果。

【思考：引導學生對操作結果加以提煉，進行數學表達。10個蘋果，每人分3個，可以分給3人，還剩1個。從圖形表征到算式表征，提出有余數的除法算式，展開讀寫認知，結合平均分的過程與結果，在抽象的算式與直觀的操作之間建立聯系，溝通有余數除法算式的算理，理解其含義，這樣的教學活動更利于學生形成初次的有余數除法的算式表達，建立有余數除法的算式模型。】

片斷三：在“擺小棒”的數學實驗中探究余數與除數的關系

1.動手做：“用12、13、14根小棒擺正方形”。

師：佩奇分完了蘋果，又在做什么了？他在擺小棒！

佩奇：我用4根小棒擺1個正方形，8根小棒擺2個正方形。像這樣用12、13、14根小棒擺正方形，結果會怎樣呢？

師：你們會和佩奇一起來探究這個問題嗎？我們來動手做一做。

師：同桌合作，先用小棒擺一擺，根據結果寫算式，填在表格里，完成后，同桌互相交流你們的想法。

教師巡視，了解學生用小棒擺正方形的過程和結果。

師：這些擺法你都看得懂嗎？都對嗎？誰來給大家完整地介紹一下？

學生介紹擺法和記錄情況（如圖）。

師：你們也是這樣擺的嗎？

師：這些商表示什么？余數呢？

生：商表示正方形的個數，余數表示剩下的小棒根數。

2.靜心想：用“15、16根小棒擺正方形”。

師：觀察以上這些算式，你有什么發現嗎？如果用15根小棒擺正方形結果會怎樣？用16根小棒呢？

挑戰：你能不用小棒，直接想一想，寫出算式嗎？在《作業單》上試一試。

教師巡視，收集學生資源。

師：老師收集了兩份作業，比較一下，有什么相同和不同？

生：15除以4的算式和結果是相同的，16除以4的結果不同。

師：（圈出15的兩個算式）沒有擺小棒，是怎么想到15根可以擺成3個正方形，還剩3根的呢？

生：可以根據14根來想，因為15根比14根多1根，14根可以擺3個正方形，余2根，那么15根就還是可以擺3個正方形，余3根。

師：你真有辦法，不用小棒，根據14根就能直接推想出15根的結果。

師：是啊！15比14多1根，可以擺3個正方形，還剩3根。算式是：15÷4=3（個）……3（根）。

師：（圈出16的兩個算式）關于16根，兩個算式結果不一樣，你們贊同誰的呢？為什么？

生1：余數不能是4。因為只要滿4根就可以擺成一個正方形。

生2：剩下的只能是不夠擺的，不滿4根的，也就是余數要比4小，不能是4。

生3：在這里，剩下的根數只會是1、2、3根，不會是4根。

師：把這4根再擺成一個正方形，所以，商3變成了4，現在的余數是幾？（0）余數是0，可以省略不寫。

形成算式：16÷4=4（個）。

3.揭示余數和除數的關系。

師：小棒根數在變，余數也在變，這里的余數大小有什么秘密呢？同桌互相說一說。

感悟：余數可能是1、2、3，不能是4，余數比4小。

師：在除法算式中，余數和除數有怎樣的關系呢？

生：余數都比除數小。

師：如果繼續擺，17÷4，余數是幾呢？18÷4？19÷4？20÷4呢？

學生再次感悟余數比除數小。

【思考：引導學生理解“余數要比除數小”，這是本課難點。教師仍采用數學實驗的方式推進教學，在積累學生操作經驗的同時更要激活思維、促進表達、深化認識，從而突破難點。基于以上思考，把例2擺小棒的活動切割成“動手做”和“精心想”兩塊，按照第一次實驗的展開方式進行，同桌合作擺一擺，記錄數據結果，數學算式表達。“用15、16根小棒擺正方形，結果又怎樣？這一次你能不用小棒，直接想一想，寫出算式嗎？”這里的想不是毫無依據地想，是基于動手做經驗的推想，因為15根比14根多1根，所以就比14根多剩余1根，由此推理出余數是3。用16根擺正方形的結果呢？仍然借助操作經驗繼續推想，但學生的想法出現了矛盾沖突，為什么余數不能是4呢？這是一個突破教學難點的重要問題，組織學生展開充分思辨，發現滿4根又可以擺成一個正方形，那么余數只可能是哪些數？繼而發現余數與除數之間的關系。從實驗操作到理性推想，動靜有機結合，學生的成功動機得到瞬時激發，知識難點得到有效突破，思維走向更深處。】

片斷四：在數學游戲中再次感悟余數與除數的關系

師：做游戲的時間到了，同學們喜歡吹泡泡嗎？泡泡很神奇，藏在了大屏幕里，讓我來吹一吹。你們也想試一試嗎？

師：數一數，吹出了6個泡泡，每次拍3個，幾次拍完？

生：2次。

師：吹出了8個泡泡，每次拍3個，有剩余嗎？剩幾個？

生：剩2個。

師：還想吹嗎？為了吹出更多的泡泡，我建議大家做一次深呼吸，泡泡多得數不清，但還是每次拍3個，如果最后有剩余，可能會剩幾個？

師：你們是怎樣想的？能用今天學到的知識告訴大家嗎？

生：可能剩1個或者2個，一定比3小，因為在除法算式中，余數都比除數小。

【思考：數學游戲的設計是對“余數比除數小”知識的再一次感知和應用，吹泡泡的活動環節，從趣味角度看，學生參與主動性強，從思維角度看，深刻而且敏捷，緊扣難點，在游戲互動中進一步加深理解余數的意義，實現知識的建模。

兩次數學實驗的設計，完善了學生對平均分的認知建構，認識了余數，并理解了余數與除數的關系，實現了知識的建模過程，內容整體推進，活動有序進行。實驗方式的展開，有利于學生把數與形很好地結合起來，把操作和思維自然地融合起來，把演繹和歸納合理地運用起來，數學實驗是邊做邊想的過程，讓思維在困頓處慢一點，在爭鳴處清一點，在生長處活一點，數學實驗的學習方式打開了學生的思維活動軌跡，教育的魅力因此得以彰顯。】