“順學(xué)而導(dǎo)”理念下的小學(xué)數(shù)學(xué)教學(xué)策略

馬婷

[摘? 要] “順學(xué)而導(dǎo)”是新課程改革所提倡的一種遵循兒童認(rèn)知心理和求知規(guī)律的教學(xué)方式。教師是學(xué)生學(xué)習(xí)的引導(dǎo)者。教師的“導(dǎo)”，要適時(shí)、適當(dāng)、適量，讓學(xué)生從“被動(dòng)”到“主動(dòng)”，從“會(huì)學(xué)”到“學(xué)會(huì)”。教師應(yīng)該促使學(xué)生在課堂上進(jìn)行高效化學(xué)習(xí)，從而構(gòu)建靈性課堂。因此，在課堂教學(xué)中，教師應(yīng)注重引導(dǎo)學(xué)生認(rèn)知數(shù)學(xué)、探究數(shù)學(xué)以及思考數(shù)學(xué)，“導(dǎo)”在認(rèn)知生長(zhǎng)處、知識(shí)構(gòu)建處和思維升華處，促進(jìn)學(xué)生真正掌握數(shù)學(xué)本質(zhì)內(nèi)涵，獲得更加豐富和生動(dòng)的學(xué)習(xí)體驗(yàn)。

[關(guān)鍵詞] 小學(xué)數(shù)學(xué);順學(xué)而導(dǎo);教學(xué)策略;以生為本;因?qū)W而教

“順學(xué)而導(dǎo)”課堂是“以學(xué)為本、以生為本”教育理念的體現(xiàn)，是教師的“主導(dǎo)”與學(xué)生的“主體”相映生輝的課堂表現(xiàn)。其中，“學(xué)”是順應(yīng)學(xué)情、關(guān)注學(xué)生學(xué)習(xí)基礎(chǔ);“導(dǎo)”是啟發(fā)引導(dǎo)、點(diǎn)撥引導(dǎo)和釋疑解惑。“順學(xué)而導(dǎo)”的關(guān)鍵在于“導(dǎo)”，教師應(yīng)關(guān)注學(xué)生的學(xué)習(xí)基礎(chǔ)、學(xué)習(xí)方法，要“想學(xué)生所想，研教學(xué)之法”。在順應(yīng)學(xué)情的基礎(chǔ)上，“導(dǎo)”得適時(shí)，“導(dǎo)” 得恰當(dāng)，“導(dǎo)”得自然，才能真正促進(jìn)學(xué)生高效學(xué)習(xí)。下面筆者以“角的初步認(rèn)識(shí)”一課教學(xué)為例，具體探討在課堂中如何順學(xué)而導(dǎo)，促進(jìn)學(xué)生的深度學(xué)習(xí)。

一、注重?cái)?shù)學(xué)認(rèn)知，“導(dǎo)”在“生長(zhǎng)處”

這里所說(shuō)的“認(rèn)知”，是指具備的生活經(jīng)驗(yàn)、數(shù)學(xué)知識(shí)以及一定程度上的解決問(wèn)題的能力。對(duì)于學(xué)生而言，學(xué)習(xí)新知的過(guò)程，就是通過(guò)構(gòu)建新舊認(rèn)知之間的聯(lián)系，對(duì)知識(shí)體系進(jìn)行重構(gòu)的過(guò)程。新知實(shí)質(zhì)上是針對(duì)舊知識(shí)而言的一種擴(kuò)展與延伸。教師在數(shù)學(xué)課堂教學(xué)中，只有基于學(xué)生的認(rèn)知起點(diǎn)順學(xué)而導(dǎo)，才能更有效促進(jìn)學(xué)生對(duì)數(shù)學(xué)知識(shí)的接收。

“角”是最基本的幾何圖形之一，也是學(xué)生認(rèn)識(shí)其他幾何圖形的基礎(chǔ)。在二年級(jí)學(xué)生的生活與經(jīng)驗(yàn)認(rèn)知中，他們認(rèn)為“角”是物體頂端的尖銳部分，正如點(diǎn)沒(méi)有大小、線沒(méi)有粗細(xì)一樣，他們對(duì)于數(shù)學(xué)概念中“角”的認(rèn)知是比較抽象的，也無(wú)法感知與觸摸到的。所以數(shù)學(xué)教學(xué)要重視學(xué)生的生活經(jīng)驗(yàn)，順學(xué)而導(dǎo)，幫助他們對(duì)“角”建立正確的表象，這是促進(jìn)學(xué)生從感性認(rèn)識(shí)向理性認(rèn)知過(guò)渡的關(guān)鍵。

在課堂中，筆者首先利用課件出示了一個(gè)三角尺，并提問(wèn)：“你們能在三角尺的面上找出角嗎？”讓學(xué)生上臺(tái)在屏幕上指出，結(jié)果發(fā)現(xiàn)很多學(xué)生認(rèn)為三角尺的一個(gè)頂點(diǎn)處就是角，對(duì)于學(xué)生的錯(cuò)誤認(rèn)知筆者并未點(diǎn)明，而是將頂點(diǎn)處用紅色圓圈標(biāo)注出來(lái)，然后將三角尺其余部位全部隱去。筆者問(wèn)：“那么，這還是角嗎？”學(xué)生齊聲回答“不是！”這顯然不是“角”，而是一個(gè)“點(diǎn)”。那么有了“點(diǎn)”，如何能得到“角”呢？此時(shí)，筆者利用課件沿三角尺隱去的一個(gè)角描出兩條線，同時(shí)，課件閃爍“角”的頂點(diǎn)。筆者試圖以這種變化讓學(xué)生發(fā)現(xiàn)：“角”實(shí)質(zhì)上是從一個(gè)點(diǎn)出發(fā)的兩條線組成的圖形。在數(shù)學(xué)中筆者們給它標(biāo)上一段短的弧線，作為“角”的標(biāo)記。筆者接著讓學(xué)生拿出自己的三角尺，跟著筆者一起在空中完整地畫出一個(gè)角，也即從角的頂點(diǎn)開(kāi)始，往任意方向畫出一條線，再往任意另一個(gè)方向畫一條線，最后用手勢(shì)給這個(gè)夾角標(biāo)上弧線。（圖1）

在此基礎(chǔ)上，筆者讓學(xué)生找出三角尺的另外兩個(gè)角，為了便于更好地觀察，筆者要求學(xué)生將這些角全部標(biāo)注出來(lái)，并仔細(xì)觀察這些圖形有什么共同點(diǎn)。最后他們發(fā)現(xiàn)這些角全部都是從一個(gè)點(diǎn)開(kāi)始（課件上閃爍的角的頂點(diǎn)），且它們都有兩條直線（課件閃爍的角的直線）。至此，學(xué)生便完成了角的表象認(rèn)知。（圖2）

在這一階段的教學(xué)過(guò)程中，當(dāng)發(fā)現(xiàn)學(xué)生誤將“頂點(diǎn)”視為“角”這個(gè)錯(cuò)誤時(shí)，筆者并未直接指出，而是基于他們的錯(cuò)誤認(rèn)知，順學(xué)而導(dǎo)，通過(guò)隱去三角尺其余的部分，讓他們主動(dòng)認(rèn)識(shí)到那只是一個(gè)“點(diǎn)”。在此基礎(chǔ)上，筆者通過(guò)畫“角”的方式，讓學(xué)生對(duì)錯(cuò)誤經(jīng)驗(yàn)進(jìn)行修正，意識(shí)到“角”中“點(diǎn)”與“邊”的關(guān)系，并從中找到角的共同特點(diǎn)。顯而易見(jiàn)，這樣的授課方式，可以為學(xué)生進(jìn)一步學(xué)習(xí)角的概念埋下伏筆。

二、注重?cái)?shù)學(xué)探究，“導(dǎo)”在“構(gòu)建處”

在數(shù)學(xué)課堂中基于學(xué)生的實(shí)際情況開(kāi)展探究活動(dòng)教學(xué)是十分重要的。順學(xué)而導(dǎo)，要求教師能準(zhǔn)確把握學(xué)生的實(shí)際情況，并積極尋找“導(dǎo)”的最佳方式，引導(dǎo)學(xué)生對(duì)數(shù)學(xué)問(wèn)題展開(kāi)全面深入探究，并在數(shù)學(xué)探究過(guò)程中自主完成對(duì)數(shù)學(xué)新知識(shí)體系的構(gòu)建。在“角”這一概念的構(gòu)建過(guò)程中，一些學(xué)生會(huì)認(rèn)為“角”的“邊”越長(zhǎng)，“角”就越大，他們將“角”的兩邊視為線段，并根據(jù)線段的長(zhǎng)短來(lái)判斷角的大小。同時(shí)，他們更傾向于根據(jù)圖形的表面大小來(lái)判斷角的大小。因此，引導(dǎo)學(xué)生深入探究角的大小與兩條線張開(kāi)程度的本質(zhì)屬性特征是本節(jié)課教學(xué)的重點(diǎn)。筆者在教學(xué)過(guò)程中進(jìn)行了如下設(shè)計(jì)：

讓學(xué)生利用兩支小棒擺成一個(gè)任意大小的角，然后跟著老師一起玩“變、變、變”的游戲，將角的大小變大一點(diǎn)、再變大點(diǎn)。學(xué)生跟著老師一起操作與體驗(yàn)。將角的兩邊慢慢地拉開(kāi)，這樣角就變大了。接著將角的兩邊合攏一些，這樣角就變小了。學(xué)生通過(guò)游戲?qū)堑拇笮∮辛顺醪降母杏X(jué)，在此基礎(chǔ)上，再讓學(xué)生繼續(xù)觀察，即利用課件的動(dòng)態(tài)演示來(lái)表現(xiàn)角的一邊在移動(dòng)過(guò)程中構(gòu)成大小不同的角。在這一過(guò)程中學(xué)生又有了新的體驗(yàn)，他們發(fā)現(xiàn)在活動(dòng)角的過(guò)程中，角的頂點(diǎn)是固定不動(dòng)的，邊是圍繞著角的頂點(diǎn)在轉(zhuǎn)動(dòng)，當(dāng)角的兩條邊張開(kāi)得越大，角就越大，相反，張開(kāi)得越小，角就越小。可見(jiàn)角的大小實(shí)際上是與兩條邊張開(kāi)的程度有關(guān)。

在這一個(gè)環(huán)節(jié)中，利用“活動(dòng)角”作為學(xué)生理解角的大小的載體，突破了“靜態(tài)角”對(duì)學(xué)生構(gòu)建角概念造成的干擾。通過(guò)游戲和課件的動(dòng)態(tài)演示，讓學(xué)生將注意力集中到角的大小與角的邊的關(guān)系上，并在頭腦中不斷積累對(duì)角的大小的感悟，并從中歸納總結(jié)出掰開(kāi)來(lái)角變大、合攏來(lái)角變小的規(guī)律。這些真實(shí)體驗(yàn)促進(jìn)了學(xué)生對(duì)角的大小的正面感悟與空間感知。

三、注重?cái)?shù)學(xué)思考，“導(dǎo)”在“升華處”

對(duì)于小學(xué)生而言，他們的思維還處于過(guò)渡時(shí)期，經(jīng)常會(huì)出現(xiàn)思維瓶頸，以及思維內(nèi)容與表達(dá)能力不匹配的現(xiàn)象。學(xué)生思維的升華，需要依靠教師的有效引導(dǎo)才能完成。因此，教師要基于學(xué)生的學(xué)習(xí)進(jìn)度，適時(shí)對(duì)學(xué)生的思維進(jìn)行點(diǎn)撥，使其思維瓶頸得以突破，將其引領(lǐng)到數(shù)學(xué)知識(shí)的縱深處。

在引導(dǎo)學(xué)生完成了對(duì)角的大小概念的構(gòu)建后，針對(duì)學(xué)生根據(jù)圖形的表面大小判斷角的大小的思維誤區(qū)，筆者嘗試進(jìn)行進(jìn)一步正面引導(dǎo)，強(qiáng)化學(xué)生對(duì)角的大小的感悟，并通過(guò)比較辨析，促進(jìn)學(xué)生思考，使其在思考中形成更多感悟。筆者的教學(xué)設(shè)計(jì)如下：

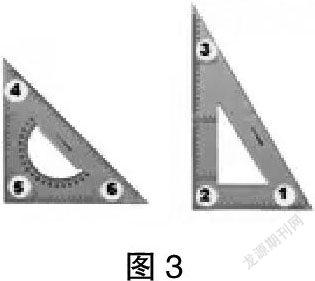
出示兩把三角尺教具，每把三角尺有三個(gè)角，兩把一共有六個(gè)角。（圖3）

接下來(lái)通過(guò)開(kāi)展“猜一猜”的游戲活動(dòng)，教師在黑板上畫出幾個(gè)角，讓學(xué)生猜一猜教師畫出的角的大小與兩把三角尺中的幾號(hào)角大小一樣。

出示第一個(gè)角：（圖4）

通過(guò)直觀判斷，學(xué)生認(rèn)為圖4中的角與③號(hào)角一樣大，那么該如何驗(yàn)證其正確性呢？有的學(xué)生提出將三角尺教具拿上去和圖4中的角比一比，如果能重疊就說(shuō)明是一樣大的。學(xué)生上臺(tái)進(jìn)行操作，發(fā)現(xiàn)這兩個(gè)角的頂點(diǎn)重合時(shí)，兩條邊也分別重合，這說(shuō)明角的兩條邊張開(kāi)一樣大。因此，圖4中的角和③號(hào)角一樣大。

學(xué)生剛才使用的是老師的三角尺教具進(jìn)行對(duì)比，那么如果換用他們自己手中的小三角尺呢？結(jié)果又會(huì)是怎樣的？有的學(xué)生猜測(cè)是一樣大的。那么如何驗(yàn)證呢？在學(xué)生猜測(cè)后，筆者繼續(xù)引導(dǎo)學(xué)生繼續(xù)利用重疊法進(jìn)行驗(yàn)證，即將教師三角尺教具的③號(hào)角與學(xué)生的小三角尺的③號(hào)角進(jìn)行對(duì)比，結(jié)果發(fā)現(xiàn)，它們的兩條邊張開(kāi)一樣大。因此它們的③號(hào)角的大小一樣。

數(shù)學(xué)家波利亞（George Polya，1887—1985）曾說(shuō)過(guò)，學(xué)生學(xué)習(xí)知識(shí)的最佳途徑是由他們自己思考與發(fā)現(xiàn)。因?yàn)檫@種發(fā)現(xiàn)最有利于促進(jìn)學(xué)生的深層學(xué)習(xí)能力與認(rèn)知深度。在課堂上，教師注意順應(yīng)學(xué)生的認(rèn)知心理，并利用重疊法引導(dǎo)學(xué)生比較教師所畫角與③號(hào)角大小、教師三角尺教具與學(xué)生學(xué)具三角尺教具的③號(hào)角大小，使其將關(guān)注的焦點(diǎn)集中在兩條邊的張開(kāi)程度上。到這個(gè)階段，學(xué)生已經(jīng)突破了思維的瓶頸，在一定程度上理解角的大小本質(zhì)了。這樣的“導(dǎo)”與“學(xué)”，對(duì)于學(xué)生感悟角的概念本質(zhì)和后續(xù)的學(xué)習(xí)大有裨益。

四、結(jié)束語(yǔ)

著名教育家杜威曾說(shuō)過(guò)：“教育就是經(jīng)驗(yàn)的改造或改組。”新課程提倡要尊重兒童，不僅要尊重兒童的思維動(dòng)態(tài)，更要尊重的是兒童的生活經(jīng)驗(yàn)與認(rèn)知缺陷。教師應(yīng)該基于兒童的學(xué)習(xí)進(jìn)展，讓學(xué)生在數(shù)學(xué)學(xué)習(xí)過(guò)程中完成對(duì)數(shù)學(xué)知識(shí)的自主構(gòu)建以及不斷修正模糊的經(jīng)驗(yàn)，促進(jìn)數(shù)學(xué)思維發(fā)展。筆者認(rèn)為，這樣的教學(xué)才是新課程所呼喚的，兒童所喜歡的，也是數(shù)學(xué)教師們應(yīng)畢生所追求的。

2080501705269