挖掘習題內涵 滲透數學文化

梁玲智

[摘? 要] 引導學生探究“楊輝三角”，發現數字之間的規律，感受“楊輝三角”的美，了解“楊輝三角”在數學中的應用。教師應該采取有效的教學策略，設計與習題相關的問題，幫助學生在問題解決中感受數學文化，在規律探究中欣賞數學文化。

[關鍵詞] 習題教學;數學文化;楊輝三角

一、教學背景

數學是人類文化的重要組成部分，數學文化是數學教學不可分割的一部分。人教版數學教材里編排了豐富的數學文化知識，除了在“你知道嗎”欄目集中呈現外，練習題里也有不少和數學文化有關的題目。如六年級上冊第八單元《數與形》的練習里，就有一道關于“楊輝三角”的題目。

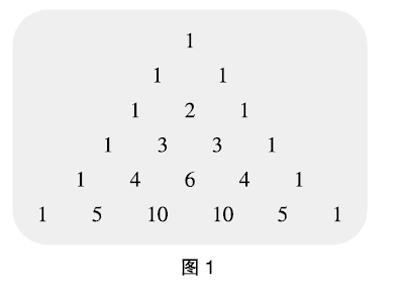
我國宋代數學家楊輝在公元1261年撰寫了《詳解九章算法》，楊輝在這本著作中畫了一個由數構成的三角形圖，我們把它稱為“楊輝三角”。你能發現下面（圖1）與“楊輝三角”圖對應的數字三角形表中各數之間的關系嗎？你能按照發現的規律把這個三角形表繼續寫下去嗎？試試看。

“楊輝三角”是我國南宋數學家楊輝的一個重要數學研究成果，是二項式系數在三角形中的一種幾何排列。它把二項式系數排成三角形的形式，把組合數內在的一些代數性質直觀地從圖形中體現出來，是一種離散型的數與形的結合。

在數學教學中滲透數學文化，能“幫助學生了解數學在人類文明發展中的作用，激發數學學習興趣，感受數學家治學的嚴謹，欣賞數學的優美”。如果僅按照題目的要求，讓學生發現數之間的關系并按照發現的規律繼續寫下去，學生并不能體會“楊輝三角”的偉大，也不能理解其在數學史上為什么會具有如此重要的地位。所以，教師應該采取有效的教學策略，設計與習題相關的問題，幫助學生在問題解決中感受數學文化，在規律探究中欣賞數學文化。

二、教學實踐

1. 發現規律

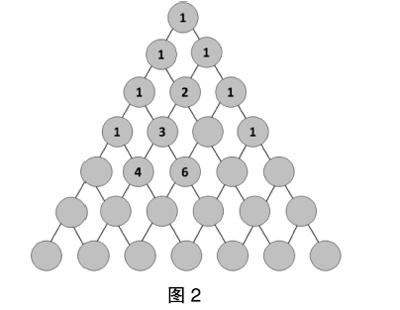
逐層出示圖2。

師：這是一張三角形的表。把數字排成三角形形狀，是我國南宋末年數學家楊輝的創舉。數學史上把這樣的三角形表稱為“楊輝三角”（板書）。大家觀察一下，“楊輝三角”中數字的排列有什么規律？

生答（略）。

師：請大家按照發現的規律，在空的圓圈里填上適當的數。

學生操作，教師根據學生的匯報把三角形表填完整。（圖略）

【設計意圖】 觀察“楊輝三角”，發現數字排列的規律，是欣賞數學文化的開始。相比讓學生直接觀察完整的前6行數據，或者由教師直接介紹規律，本教學環節的探究活動使學生從被動接受者轉變為主動發現者，更能激發學生的學習積極性。從而使學生發現奇妙的數學規律，親近數學文化，悅納數學文化。

2. 感受“楊輝三角”的美

師：有的同學在嘀咕了，這么簡單的數字排列，居然被稱為創舉？同學們，雖然“楊輝三角”的數字和排列規律都非常簡單，但在數學學習中是非常有用的。雖然相關的一些知識要到初中才學習，但“楊輝三角”中一些奇妙的規律，我們小學生也能去探究。

（1）和2的冪的關系

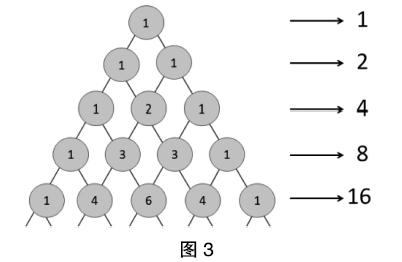
師：請大家橫著把前5行每一行數分別相加。

學生操作，反饋，在PPT上呈現答案（圖3）。

師：有什么發現？

生1：都是兩倍的關系。

生2：后面的數都是前面數的兩倍。

師：能把這些數寫成2的幾次方的形式嗎？

生：2等于21，4等于22，8等于23，16等于24。

師：猜一猜，下一行數的和是幾？

生1：32。16×2=32。

生2：32也就是2的5次方。

師：讓我們驗證一下。（學生驗證）正確！在數學上，2的0次方就是1。這里每一行的數的和，都可以寫成2的幾次方形式。實際上，“楊輝三角”最初就是用來解決兩個數或字母相加和的幾次方的問題的。

（2）和11的冪的關系

師：你們能口算11的平方嗎？

學生馬上回答：121。

師：11的3次方呢？

學生遲疑，有的口算，有的列豎式計算。過一會兒，報出答案：1331。

教師微笑著指指“楊輝三角”的第4行，學生一片嘩然。

師：11的4次方呢？

生：14641！

師：你怎么算得這么快？

生：楊輝三角的第5行就是這個數。

師：真會思考。我們用計算器驗證一下。（驗證）正確。

師：11的5次方呢？

生：151051！

教師用計算器計算14641乘11，得到161051。學生發出“啊”的聲音。

師：怎么回事？

生：我知道了。這里的6+4等于10，其實是要向前一位進1的。然后4加6等于10，加上1是11，寫1進1;5加1等于6，所以是161051。

教師在PPT上演示，得出楊輝三角中的數字是正確的，但由于要滿十進一，所以最后寫出來的數發生了變化。

（3）和三角形數、四面體數的關系

教師演示（圖4-1）：斜著看，有什么發現？

生：第一列都是1，第二列一個一個大起來，第三列是加2，加3，加4，第四列是加3，加6，加10……都是有規律的。

師：右邊（或左邊）第二列都是自然數序列，右邊（或左邊）第三列都是三角形數序列（出示圖4-2）。請大家翻到書本第109頁，看到練習二十二第2題。

師：接下來的一個三角形數是15，請同學們用圖表示出15。（學生畫，略）

師：下兩個三角形數分別是什么？請畫圖表示。

學生操作（略）。

師：右邊（或左邊）第四列都是四面體數，我們欣賞一下（圖4-3）。

3. 楊輝三角的應用

師：“楊輝三角”利用數與形的巧妙統一，在解決一些數學問題時可以起到很好的作用。我們來看下面的例子：

從A到B之間有很多交叉路口。如果只能向右或向下走，那么從A到B一共有幾種不同的走法？（如圖5-1）

學生嘗試操作，會發現比較困難。

教師提示：把圖順時針旋轉45°，轉化為類似“楊輝三角”的圖形，把每一個交叉點上的走法標出來，用“楊輝三角”的知識來解決（圖5-2）。

小結：楊輝三角中的奧秘還有很多，等待同學們進一步去發現。

4. 楊輝及“楊輝三角”在數學史上的地位

PPT出示，略。

【設計意圖】在習題教學中滲透數學文化，要根據學生的學習基礎展開，不過分拔高，不偏離教學目標。“楊輝三角”，本意是解決二項式系數問題的，但其中還蘊藏著很多奇妙的規律。除文中呈現的之外，還有與斐波那契數列之間的聯系，與組合數之間的聯系等。這些知識，有些超出了六年級學生的認知范圍，有些和本單元《數與形》的教學目標不相符，所以沒在教學中呈現。

三、教學體會

“楊輝三角”是中國古代數學史上光輝燦爛的一頁。引領學生探尋“楊輝三角”的奧秘，不僅能加深學生對“楊輝三角”的認識，還可以讓學生更好地感受數與形之間的相互作用，受到數學文化的熏陶。如果教師能充分認識數學習題里蘊含的數學文化價值，以問題引領，讓學生經歷探究數學規律的過程，就能幫助學生更好地感受數學文化，欣賞數學文化，體會數學的思想、精神和價值。