初中高中兩相依，它山之石可攻玉*
——平幾知識在解幾中的應用

福建省廈門大學附屬實驗中學 (363123) 王亞坤 林秋林

一、問題提出

解析幾何的本質是用代數方法研究圖形的幾何性質，體現了數形結合的重要數學思想，在高考中有著重要的地位，是高考命題的熱點之一．一般來說，解析幾何綜合問題主要以圓錐曲線為載體，綜合各個模塊知識，全面考查學生分析問題、解決問題的能力，對邏輯思維能力與運算能力要求較高，有一定的難度.學生在解答解析幾何綜合問題時，習慣于先聯立直線與圓錐曲線的方程，再通過代數方法進行推理，往往導致運算量太大而不得不中途放棄．事實上，“解析幾何也是幾何”，其本身也隱含著平面幾何的思想方法.在解答某些解析幾何問題時，如果注重“初高中結合”，充分利用圖形的直觀性和平面幾何知識，靈活處理，不僅能避開繁瑣的代數運算，還能揭示問題的幾何本質.同時，借助幾何直觀，利用平面幾何的思想方法解決問題，有助于提高學生的實踐能力，提升創新意識，發展直觀想象、邏輯推理等數學學科核心素養.

二、應用舉例

1.應用“勾股定理”

例1 (2020年高考全國Ⅰ卷)已知圓M:x2+y2-2x-2y-2=0，直線l:2x+y+2=0，P為l上的動點，過點P作圓M的切線PA,PB，且切點為A,B，當|PM|·|AB|最小時，直線AB的方程為( ).

A.2x-y-1=0 B.2x+y-1=0

C.2x-y+1=0 D.2x+y+1=0

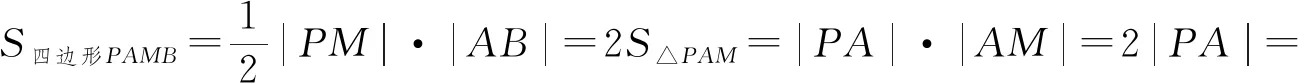
2.應用“三角形中位線”

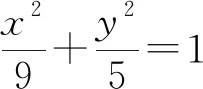
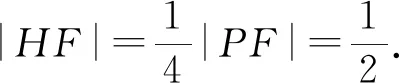
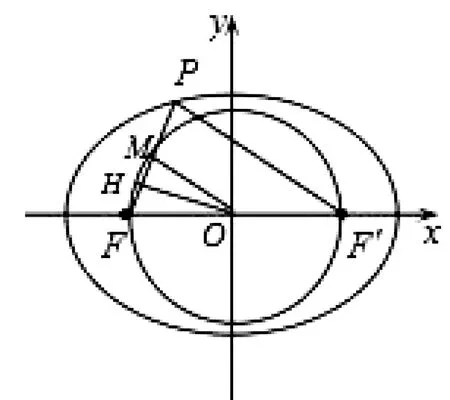
圖1

3.應用“相似三角形”

例3 (2019年高考全國Ⅰ卷)已知橢圓C的焦點為F1(-1,0),F2(1,0)，過F2的直線與C交于A,B兩點．若|AF2|=2|F2B|，|AB|=|BF1|，則C的方程為( )．

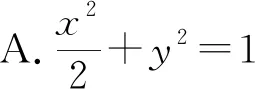
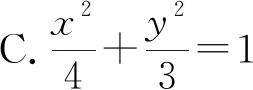
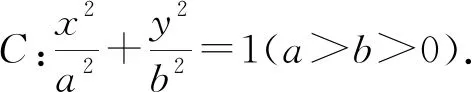
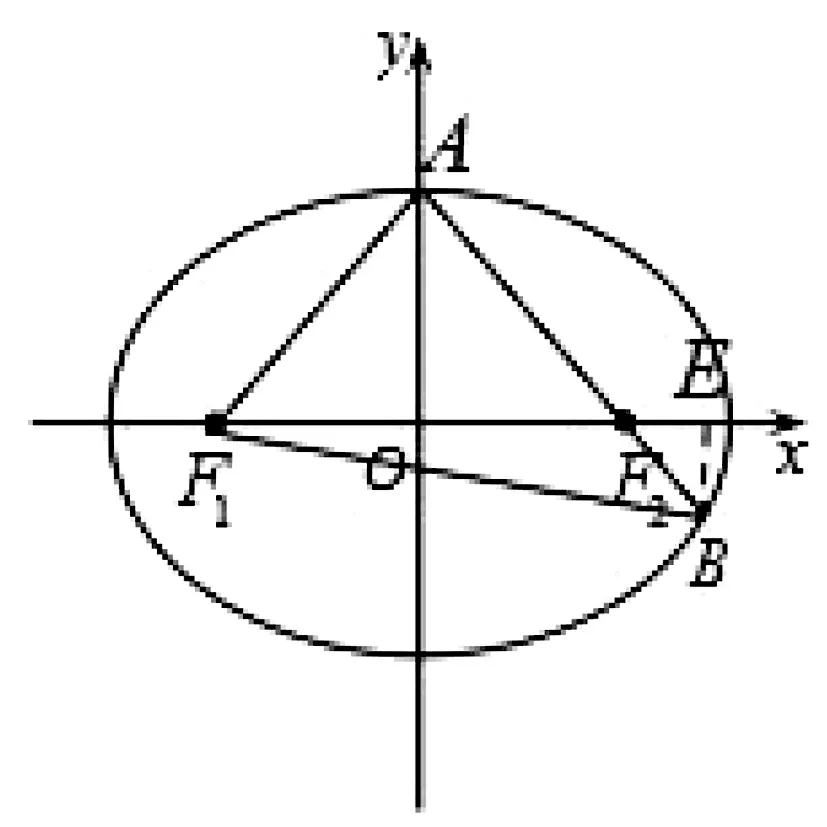
圖2

4.應用“直角三角形斜邊上的中線等于斜邊的一半”

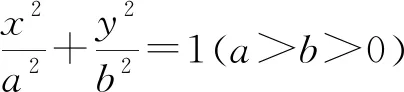
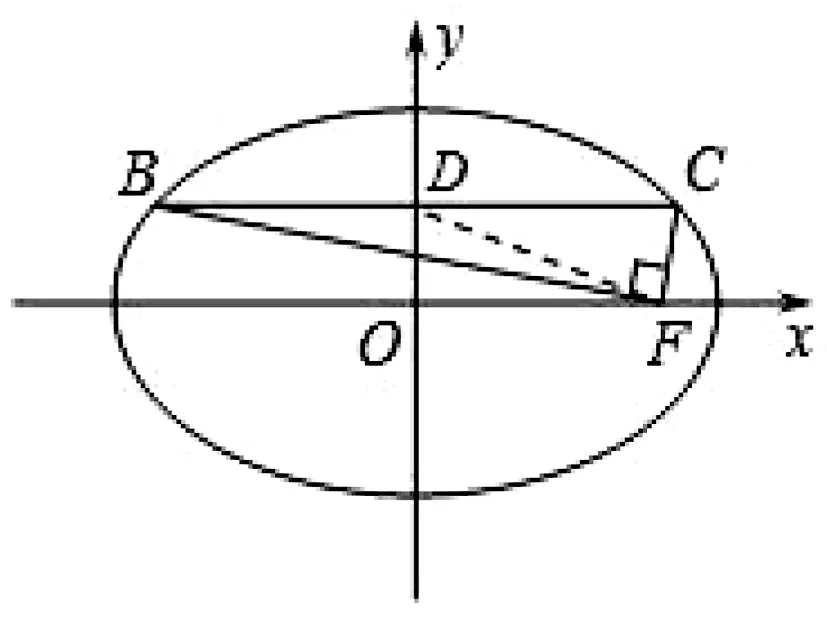
圖3

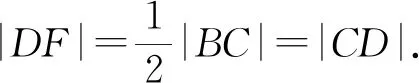
5.應用“等積法”

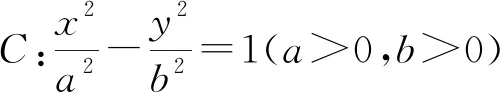
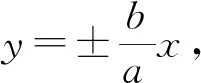
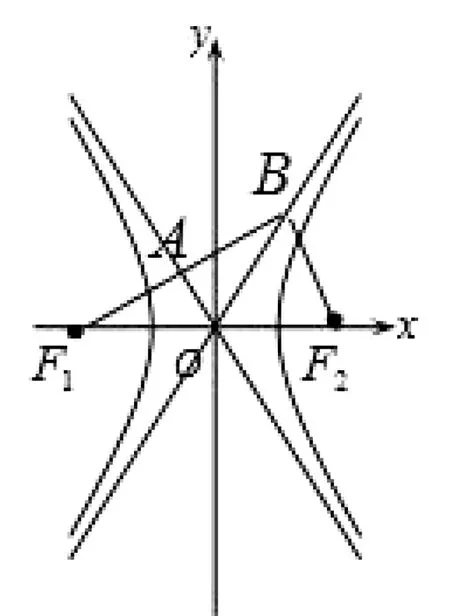
圖4

6.應用“圓的性質”

例6 (2014年高考課標Ⅱ卷)設點M(x0,1)，若在圓O:x2+y2=1上存在點N，使得∠OMN=45°，則x0的取值范圍是( ).

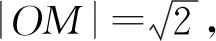
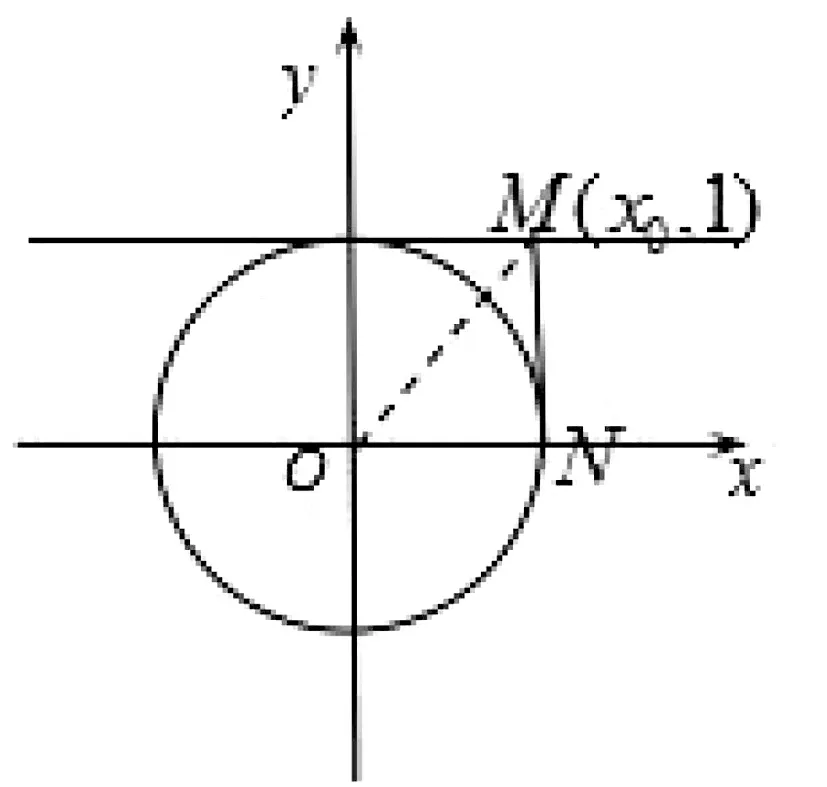
圖5

7.應用“平行線和等腰三角形的性質”

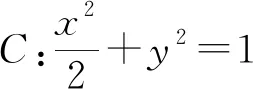
(1)當l與x軸垂直時，求直線AM的方程；

(2)設O為坐標原點，證明：∠OMA=∠OMB．

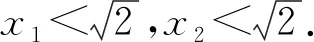
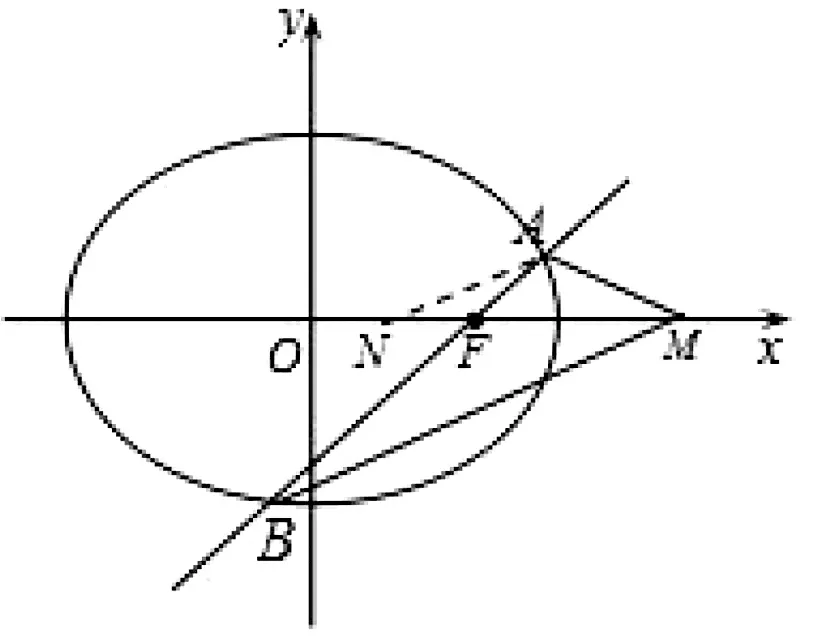
圖6

三、結語

《普通高中數學課程標準(2017)》指出：“教師要幫助學生完成從初中到高中數學學習的過渡，包括知識與技能、方法與習慣、能力與態度等方面”[1].平面幾何“討論點，直線，直線的平行和垂直，三角形，圓等.這是平面圖形中最基本、最簡單者，然而也是培養學生的幾何直觀能力和進一步用坐標法討論曲線的基礎.”[2]圓錐曲線的學習中，一般是給出它們的幾何定義后，便用數形結合的代數方法——“坐標法”來討論它們.基于此，在解答解析幾何問題時，要自始至終貫穿數形結合的思想，在圖形的研究過程中，注意代數方法的使用；在代數方法的使用過程中，加強與圖形的聯系.借助平面幾何的知識解決解析幾何問題，有助于把握問題的幾何本質，有效控制運算量.更重要的是，在解決解析幾何問題時，回歸“圓錐曲線的定義”，靈活利用圖形的直觀性和平面幾何中的相關結論，其實質就是重新審視數學概念并用概念解決問題，這是一種樸素而又重要的策略和思想，有助于使學生體會數學知識之間的有機聯系，感受數學的整體性，發展直觀想象、邏輯推理等數學學科核心素養，提升創新意識.