例談求解向量數量積問題的四種策略

江蘇省蘇州工業園區教師發展中心 (215021) 楊原明

向量數量積的運算是向量問題中的一個重要內容，經常與平面向量的模與夾角等知識交匯，表現出的題型也多種多樣，如求值、求最值、求參數范圍等．但有些學生由于各類題型缺乏科學的訓練和系統地整理，遇到此類問題還是顯得束手無策，本文介紹常用的四種方法，旨在幫助歸納整理，僅供參考．

1.提取合并：就是在給出的向量數量積條件式中，反用向量相乘的分配律，通過先部分提取向量，然后構造出新的向量數量積的形式達到轉化問題、解決問題的目的．

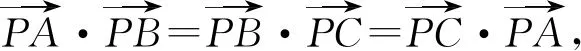
A．外心 B．內心 C．重心 D．垂心

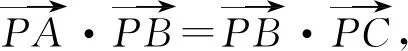
評注：由于向量運算滿足乘法的交換率，故在處理數量積問題時，經常使用提取的手段轉化問題，本題中通過對所給等式中采取移項、提取相同的向量，展示出了向量間的幾何特征，為后面的判斷提供了強力的支持．

評注：由于題目中的條件單一，怎樣用好這個條件是解題關鍵，而向量的數量積關系向三角形邊之間關系轉化就是如何得到向量平方之間的關系，其中的提取法是一個重要解題方法．

2.分解變形：在解決向量求積問題時，利用向量的加、減法法則對所給向量式進行拆分、分解、重組等轉化，使之變形到能夠利用已知條件解題為目的．

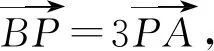
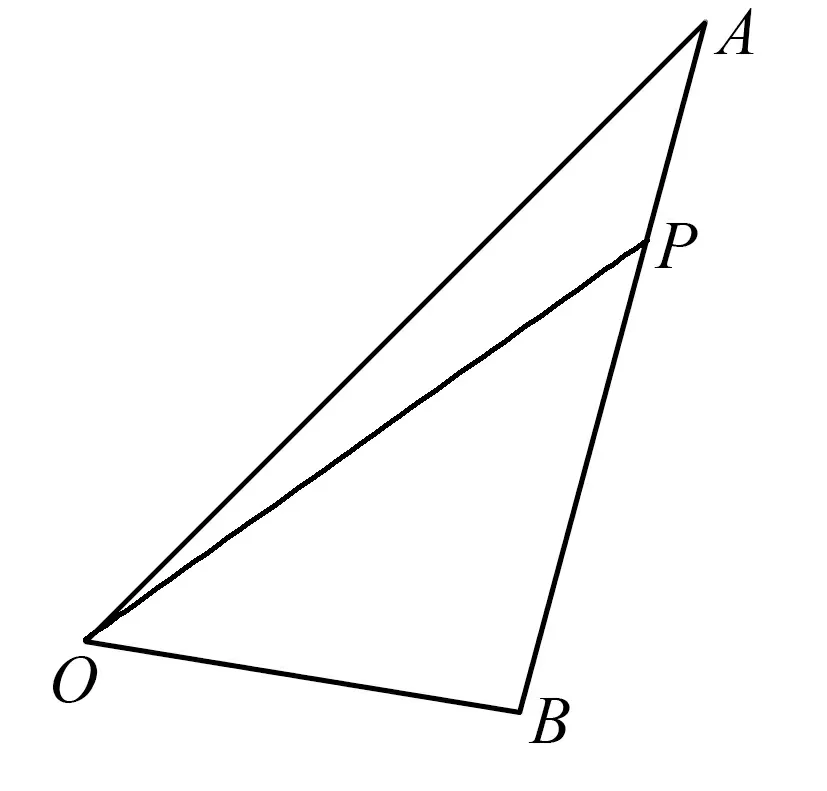
圖1

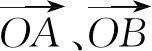
評注：在分解向量時要有目標意識，其目的是有利于運用已知的向量模和夾角等條件來解題，本題中正確的使用題設向量表示所求結論中的向量是解題關鍵．

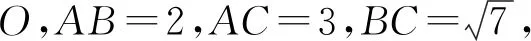
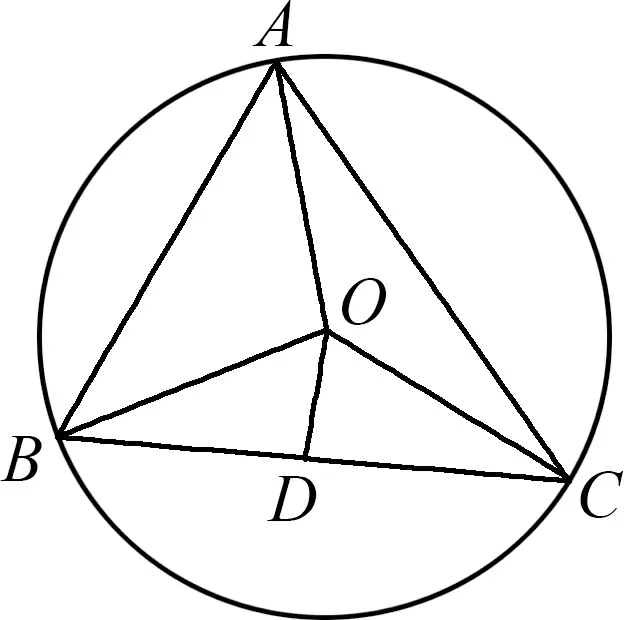
圖2

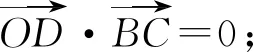
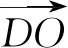
3.引參轉化：在求與向量數量積的最值問題時，可以通過引入參數，將一些變化中的向量表示出來，再用代數中求最值的方法解決問題．

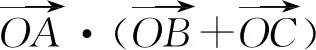
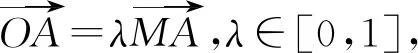
評注：如果一個動向量是在已知的向量上移動，可靈活運用共線向量的定理，引入參數，將動向量用已知向量表示出來，將動向量問題通過已知向量替換轉化，就容易達到解題目的了．

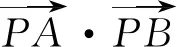
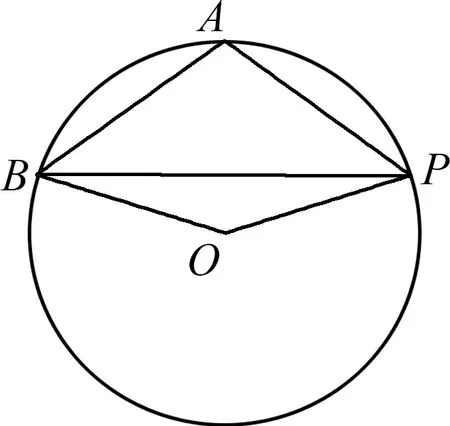
圖3

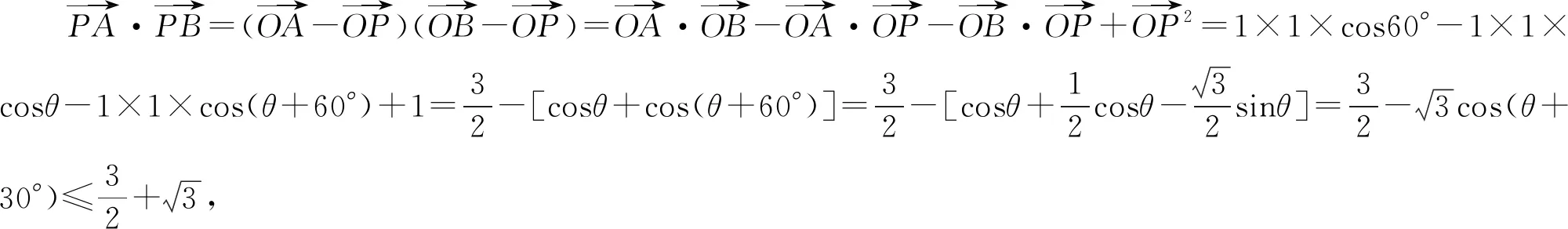
評注：對于圓(或弧)上的動向量問題，通過設角為參數，就可以將動向量與已知的向量建立聯系，然后再抓住圓心及圓的相關性質轉化待求的向量數量積，最后利用三角函數的性質解決最值問題．

4.兩邊平方：解決向量模的問題的一個重要方法就是平方運算，同樣在一些向量數量積問題中，通過對相關向量式進行兩邊平方也可以得到向量的數量積關系式，這樣就為成功解題創造了條件．

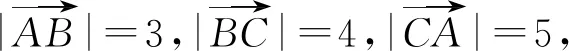
評注：本題通過認真研究題目所給的條件和待求的結論，發現了結論式其實可以由一個三項式的平方得到，這就是審題的效果．高瞻遠矚，把握問題的實質，然后用整體平方求解，圓滿高效的完成答題任務．此題還可以挖掘出△ABC是直角三角形，再利用其特點來解題．

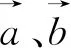
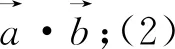
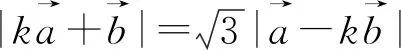
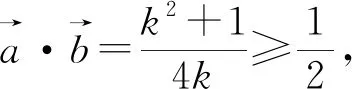
評注：由于給出的條件是向量模的等式，且要求的向量數量積是包含在模的等式中，故而求解此題的最好方法就是兩邊平方．而后面的抓住k>0，運用基本不等式求最值就是一些水到渠成、垂手可得的操作了．

以上展示了解決向量數量積問題的四種常用方法和運用技巧，但平時解題中還應該需要運用到其它方法幫助解題，并且注重精做精練，不斷總結歸納，增加知識儲備，只有這樣，我們的解題能力、思維品質才會有較大的提升．