立足教材開展探究教學的幾點思考

福建省閩清第一中學 (350800) 林 婷

數學探究是學生學習數學的一種基本方式，注重以學生為本，讓學生經歷知識的自然生成過程，經歷發現問題和解決問題的過程，是積累數學活動經驗、發展思維培養數學核心素養的重要途徑.數學具有高度抽象性的特點，未經過自主體驗、感悟與生成的“被告知”或“被模仿”的數學知識，無法在學生的腦海中留下深刻的印象.因此，在課堂教學中，教師應立足教材，以概念、原理、公式、例題等知識為載體，營造民主、和諧的氛圍，適時鋪設不同形式的探究之路，最大限度地開發學生的潛能，調動學生探索的熱情，引導學生在不斷的思考、探究與追問中自然地實現課堂的有效生成.以下筆者結合多年的數學教學實踐，談談立足教材開展探究性教學的幾點體會.

1 創設情境，喚起探究熱情

數學知識具有高度凝練性、抽象性等特點，特別是數學的高度抽象性讓學生難以體會到數學知識的意蘊，難以體會當初數學家發明創造時的“火熱的思考”.創設源于學生生活的情境會讓學生更有親近感，以此為載體的數學知識也最能給學生留下深刻的印象.因此，在數學課堂教學中，教師應在學生的“最近發展區”精心創設有思考價值的問題情境，引發學生強烈的“欲達彼岸”的心理需求與“樂此不彼”的求知欲，推動學生在具體情境中參與探究，從而實現“精彩地鋪墊，自然地生成”.

案例1 高中數學新教材(人教A版)必修第二冊“直線與平面垂直的定義”引入.

問題1 在“直線與平面平行”學習中，我們將“直線與平面平行”轉化成“直線與直線平行”研究，體現了“平面化”與“降維”思想.那么，“直線與平面垂直”是否也可以轉化成直線與某些元素之間的關系進行研究呢？

教師將書本豎放在講臺上(如圖1)，又提出如下問題.

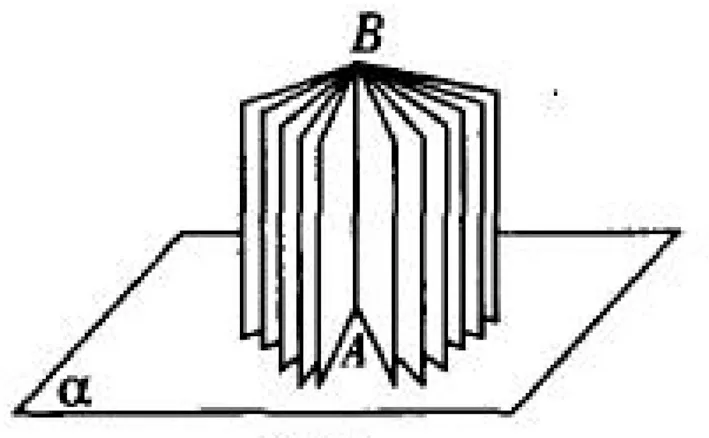
圖1

問題2 請同學們打開數學課本，把它直立在桌面上，觀察書脊所在的直線與桌面有怎樣的位置關系？

問題3 為了使書脊與桌面α垂直，書脊所在直線的AB與各書頁和桌面交線具有什么樣的位置關系？

問題4 為了使書脊與桌面α垂直，書脊所在的直線AB與桌面上任一條不過點A的直線有什么樣的位置關系？為什么？

問題5 通過以上的觀察，你認為應怎樣定義直線與平面垂直？

設計“問題情境”不僅僅是為了引出話題，更應該蘊含數學思想方法和數學本質.案例1精心創設可望、可及、直抵問題本質的真實情境，問題1滲透類比、轉化與降維思想，問題2讓學生感知直線與平面垂直的典型實例，問題3和問題4分別點出了直線AB與平面α內的直線的兩種垂直關系(相交垂直與異面垂直)，問題設計簡潔精煉卻直抵數學本質，不僅讓學生找到了知識的生長點，而且有效刺激了學生的大腦，喚起了學生探究的欲望.教師在學生已有的知識水平和生活經驗的前提下，引導學生主動、深層次地參與到問題解決的過程中，讓學生經歷觀察、實驗、分析、抽象、概括的過程.通過師生、生生之間實質性的探究活動，催生了建構概念的智慧，“直線與平面垂直”定義的生成已是水到渠成.

2 激活過程，體驗探究樂趣

在課堂教學中，教師的任務不是把現成的知識灌輸給學生，而應該讓學生體驗知識的產生與發展過程.因此，教師要圍繞課堂教學目標，在了解學生已有數學活動經驗的基礎上，通過平等對話、溝通交流，激發學生學習數學的熱情.通過觀察、操作、分析、比較、歸納、猜想、驗證等數學思維活動，引領學生在概念的形成過程、定理的推導過程、結論的揭示過程中把研究的事物從某種角度看待的本質屬性抽取出來，讓學生經歷完整的數學抽象過程，提升學生的數學抽象素養.

案例2 高中數學新教材(人教A版)必修第二冊“二面角”概念的教學片斷.

師：同學們在初中已經學習了角的概念，回顧一下角是怎么定義的？

生(眾)：從平面上的一個定點引出兩條射線，這個定點與兩條射線所組成的圖形稱為角.

師：請大家模仿平面幾何中角的概念來定義二面角.

生1：把角的概念類比到空間，定點則變成了定直線(即棱)，由定點引出的兩條射線就變成從這條棱引出的兩個半平面.

師：很好！我們把角的定義中的每一個元素升級到空間中的元素，就得到了“二面角”的概念.大家來觀察一下多媒體中不同形狀的二面角模型(教師多媒體展示二面角的各種模型，以加深學生對二面角概念的理解).

師：我們應該如何刻畫二面角的大小呢？想一想生活中有否存在二面角的實際模型？

生2：教室的墻面與地面、打開的筆記本電腦、翻開的課本都是二面角的空間模型.

師：對，請大家轉動課本的書頁，思考應該怎樣度量二面角的大小？

(學生探究、討論)

生3：二面角既然稱為“角”，就能夠用一個確定的平面角來刻畫.

師：不錯！哪一個平面角能擔負此重任呢？

師(見一些學生感到茫然，教師追問)：平面角的頂點應落在哪一個位置？角的兩條射線該如何放置，才能合理地刻畫二面角呢？

(教師讓每個學生拿出一張紙，引導學生動手操作：紙對折后是一個二面角，過棱上的一點在兩個半平面內嘗試各畫一條射線，然后讓學生觀察如何刻畫二面角的平面角.小組合作探究、交流.)

生4：如圖2，在棱l上取一點O，在半平面α、β內分別作射線OA、OB，使OA⊥l，OB⊥l，則射線OA、OB所組成的∠AOB能夠度量其大小.

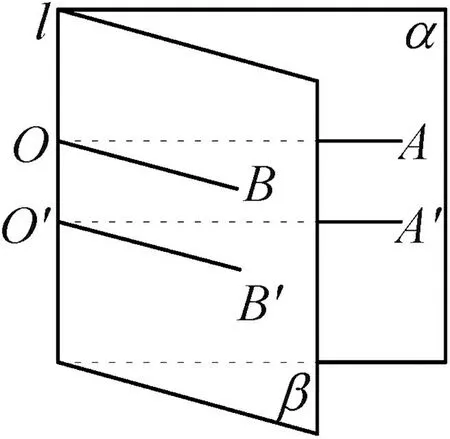
圖2

師：點O是如何確定的？能否在l上取其他的點呢？

圖2(b)是Fe3O4-C磁性空心微球的XRD譜圖，其中在2θ為30.06°、35.42°、43.02°、53.41°、56.92°和62.49°處出現了Fe3O4的6個特征衍射峰，分別對應著標準尖晶石結構的220、311、400、422、511和440晶面[10]，證明材料中主要是尖晶石結構的Fe3O4組分，且結晶良好，同時也說明硅膠核心的溶蝕過程并未造成Fe3O4組分的破壞。

生5：應該可以，我在棱l上再取點O′，在半平面α、β內作射線O′A、O′B，使O′A⊥l，O′B⊥l，依等角定理可知，∠AOB=∠AO′B，因此這樣作出的角與點O在棱l上的位置是無關的.

師：概括到位！如果把這個角叫做二面角的平面角，大家覺得合適嗎？

生6：我在棱l上取一點O，在半平面α、β內分別作射線OA、OB，使得OA、OB與直線l的夾角都為60°，射線OA、OB所組成的∠AOB也是確定的，所以我認為∠AOB也可以度量二面角大小.

師：生6說得也有道理！哪一種作法更恰當呢？

師(見沒有學生發言，教師進一步追問)：請大家將二面角的一個半平面放在桌面上，把另一個半平面繞著棱l轉動，當兩個半平面重合時，它們都落在桌面上，此時平面角分別為多少？

(學生操作、思考)

生7：當兩個半平面都落在桌面時，平面角是180°；當兩個半平面重合時，平面角是0°.只有當OA⊥l，OB⊥l時，作射線OA、OB組成的角∠AOB才是0°和180°.因此當OA⊥l，OB⊥l時，∠AOB表示二面角的平面角最合適.

“二面角”的概念是一個難點，突破難點的關鍵是利用某些具體材料進行鋪墊，當學生大腦中有了直觀的雛形后，教師再引導學生探究，從具體到抽象、從現象到本質，讓學生參與概念建構的全過程.案例2中，教師為學生營造平等的對話時空，并扮演好“穿針引線”的角色，引導學生觀察、分析，操作、交流，把學習新知的過程，變成學生“再發現”、“再創造”的過程.通過深度探究，一個個疑惑點的探析與破解，學生親身經歷“二面角的平面角”概念的建構過程，不僅掌握了研究問題的方法，而且品嘗了“數學發現”的心路歷程.思維對話的過程，正是學生的思想經過激烈的分歧和斗爭，不斷地融合統一，進而實現升華的過程.在此過程中，實現了由形到數、由具體到抽象的轉化.通過這樣的深度學習，學生對數學知識本質的理解才能更自然、更深刻，數學核心素養的培養方能落地.

3 拓展教材例習題,深化探究能力

教材中的例(習)題是經過專家精心構思、反復推敲之后選定的，具有起點低、入口寬、視角開放等特點，為教師科學合理地實施課堂教學提供了典型范例.在數學課堂教學中，教師在引導學生完成例(習)題的學習后，要有意識地引導學生對問題多角度、多層次地進行引申、拓展，為學生提供教科書之外的廣闊的探究空間，從而激發學生的學習動力，使學生的思維提高到一個由例及類的檔次，達到一題串一簇，一題聯一線的境地.經常這樣做，學生身上就能噴發出創新的“火花”，數學核心素養才能得到真正的提升.

案例3 高中數學新教材(人教A版)數學必修第一冊第101頁復習參考題3第8題.

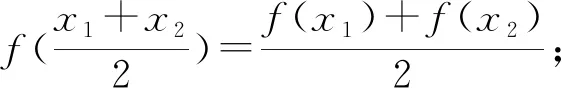
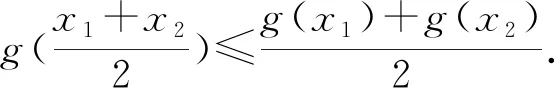
為了深度挖掘本題目背后所蘊涵的思想，展現其本質屬性，教師有意將該題留在學生學習了指數函數與對數函數后的復習課中，引導學生探究.學生證明了本題后，教師又列舉了幾類函數，引導學生歸納出結論：

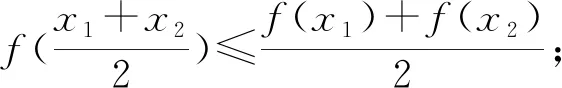
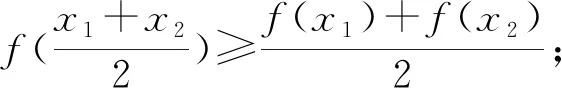
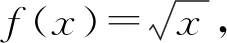
然后，教師請學生畫出這幾類函數的圖像，引導學生探究更一般的結論.學生通過總結，提煉出了凹凸函數的性質：

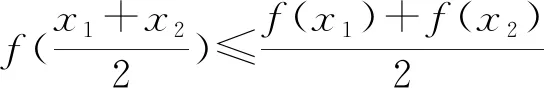
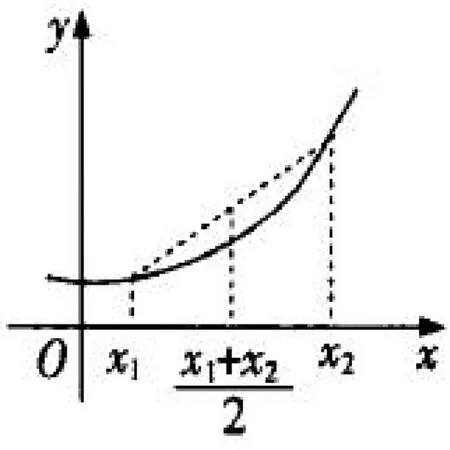
圖3

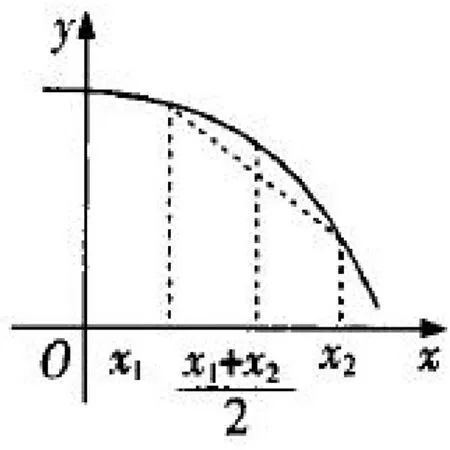
圖4

通過挖掘習題的教學功能，引導學生進行有序、科學地探究，有助于學生理解所學知識，領悟蘊涵其中的數學思想方法，生成新的“生長點”；有助于培養學生獨立思考、主動探究的學習習慣，引領學生從表層學習走向深層學習，提升數學抽象、邏輯推理、數學建模型等數學核心素養.

數學探究為學生提供了一個協同學習、互動交流的機會，有利于數學知識的“再發現”、“再創造”，有利于學生思維的深層參與，是現實且有效的學習方式.在數學課堂教學中，教師應充分發揮教材的隱性價值，富有創造性地使用教材資源，適時引導學生開展有序、科學的探究活動，引領學生在交流中探究，在探究中創新，使學生獲得非預期的生成性發展，讓數學核心素養落地生根.