學新課程標準,創設情境探究特殊與一般思想*

廣東省惠州市惠陽區崇雅實驗學校(516211) 王瑞生

教學活動中,應結合教學任務及其蘊合的數學學科核心素養設計合適的情境和問題, 引導學生用數學的眼光觀察現象、發現問題,使用恰當的數學語言描述問題,用數學的思想、方法解決問題.在問題解決的過程中,理解數學內容的本質,促進學生數學學科核心素養的形成和發展[1].

特殊與一般思想是數學的重要思想之一,數學公式、定理、法則的學習通常就是先從特殊開始,再總結歸納,后經過證明得到一般性結論,又使用一般性結論來解決相關的數學問題.這種由特殊到一般再由一般到特殊反復認識的過程,正是這一數學思想的具體體現.

數學高考中, 特殊與一般思想的考查方式通常表現為:字母表示數、歸納猜想、構造函數、應用特殊圖形、探求特殊點等等.高考試題常通過選擇題、填空題考查由特殊到一般,借助解答題的嚴謹性綜合考查特殊與一般的數學思想.

下面以2020年高考數學全國I 卷理科幾例典型試題在教學中的情境創設及“問題串”的引導,感悟特殊與一般數學思想的應用.

1 創設數學文化情境,用字母表示數的一般性

例1(2020年高考數學全國新課標I 卷理科第3 題)埃及胡夫金字塔是古代世界建筑奇跡之一,它的形狀可視為一個正四棱錐,以該四棱錐的高為邊長的正方形面積等于該四棱錐一個側面三角形的面積,則其側面三角形底邊上的高與底面正方形的邊長的比值為( )

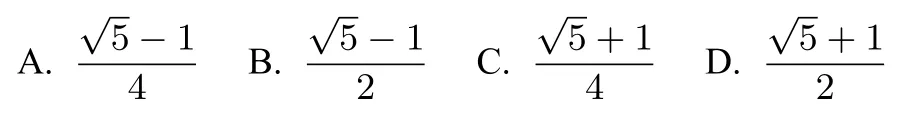
情境設計:《九章算術·商功》:“陽馬居二,鱉臑居一,不易之率也.”今稱為劉徽原理.劉徽注《九章算術》關于體積問題的論述已接觸到現代體積理論的核心問題.

陽馬: 中國古代算數中的一種幾何形體,是底面為長方形,兩個三角面與底面垂直的四棱錐體.

投影胡夫金字塔圖片.

圖1

圖2

問題1: (1)金字塔的形狀可以聯想到哪一類空間幾何體?

(2)能描述該類幾何體的結構特征嗎?

投影2020年高考數學全國新課標I 卷理科第3 題.

問題2: (1)四棱錐的高、側面三角形底邊長如何表示?

(2)探究正四棱錐的基本量的關系?

設計意圖由《九章算術》中的陽馬引入四棱錐,展示中華悠久的數學文化成就,落實立德樹人的教育目標,同時為引導同學們將胡夫金字塔直觀聯想為正四棱錐做鋪墊.

將數學文化滲透在日常教學中,引導學生了解數學的發展歷程,認識數學在科學技術、社會發展中的作用,感悟數學的價值,提升學生的科學精神、應用意識和人文素養,將數學文化融入教學,還有利于激發學生的數學學習興趣,有利于學生進一步理解數學,有利于開拓學生視野、提升數學學科核心素養[1].

通過問題1 將胡夫金字塔抽象為正四棱錐,讓學生感受現實生活問題抽象為數學模型,體現數學源于對現實世界的抽象,又服務于生活的基本理念,培養學生的直觀想象、數學建模等數學核心素養.正四棱錐是特殊的多面體,追問“能說出該幾何體的結構特征嗎? ”目的是啟發學生獨立思考,引導學生把握數學內容的本質.運用直觀感知、推理論證、度量計算等認識和探索幾何體的結構特征,探究空間幾何圖形的性質,方可建立空間概念.

該題目條件中沒有給出四棱錐的高、側面三角形底邊長的相關數據,怎么計算? 問題2 意在引導學生用字母表示高、邊長等數學量,可設正四棱錐的高為h、底面邊長為a,用字母表示數是一般性的應用.追問(2)引導學生將空間問題平面化,把線段、角看作三角形的邊、內角,通過構造直角三角形探求基本量的關系.

問題2 重在培養學生數據處理、數學運算等數學核心素養.

立體幾何初步的教學重點是幫助學生逐步形成空間觀念,應遵循從整體到局部、從具體到抽象的原則,提供豐富的實物模型呈現空間幾何體,幫助學生認識空間幾何體的結構特征,進一步掌握在平面上表示空間圖形的方法和技能[1].

2 創設現實情境,構造特殊函數

例2(2020年高考數學全國新課標I 卷理科第12 題)若2a+log2a=4b+2log4b,則( )

A.a ＞2bB.a ＜2bC.a ＞b2D.a ＜b2

情境設計: 播放視頻: 2019年4月12日,天津楊村,飛機的轟鳴聲響徹云霄,單機大仰角上升、四機向上開花……被譽為“藍天儀仗隊”的空軍八一飛行表演隊駕駛殲-10 表演機,為觀眾獻上了一場精彩的視覺盛宴.“場面太震撼了,我為祖國有這樣棒的飛機驕傲.”一位專程從山東趕來觀看表演的王先生激動地對記者說.

問題1: (1)殲-10 特技動作是集飛行員素質、數學與科技的融合,殲-10 單機大仰角上升在空中劃出一道優美的曲線,同學們會聯想到哪一類基本初等函數?

(2)了解互為反函數嗎?

問題2: 觀察等式兩邊的結構特征,應如何變形?

問題3: (1)觀察選項,對變形后的等式有何想法?

(2)觀察化歸后的不等式,發現什么?

(3)相同的作為常量,不同的a與2b作為變量,可構造函數____.

設計意圖在“我為祖國有這樣棒的飛機驕傲”的激動聲音中感受祖國的強大,培養同學們的民族自信心和自豪感,增強社會責任感;讓數學為學生形成正確人生觀、價值觀、世界觀等方面發揮獨特作用.特技“大仰角上升”形象的描繪出單調遞增的指數函數圖像,順勢引入指數函數y=ax(a ＞0且a/=1),通過追問(2),由數學概念“互為反函數”把對數函數y= logax(a ＞0 且a /= 1)和指數函數有機的結合在一起,起到承上啟下的作用.而“優美”一詞旨在讓同學們體會曲線之美到數學之美的同時,借圖象揭示函數性質,并在現實問題中利用函數構建模型,解決問題.培養學生直觀想象、數學建模等核心素養.

問題2 觀察等式的結構特征,就是有意識的讓同學們感知數與形的特點,對字母、數字、符號或文字所表達的數學關系式的結構進行觀察,培養數學觀察力是實現教學目標和提高學生數學素養的需要.同學們可以發現“等式兩邊的代數式底數雖不同,但可化為同底”,即2a+log2a=22b+log2b.

問題3 遞進式引入,引導同學們分析題干和選擇支的信息,將問題適當加工處理,構造與問題相關的數學模型,揭示其本質.

由對數函數單調性可得2a+ log2a= 22b+ log2b ＜22b+log22b,構造分別以a,2b為變化量的不等關系式,將問題引向函數性質的應用.

在此,問題(1)是方向,問題(2)就是該題的靈魂——構造特殊函數.

再次引導學生觀察: 發現兩個式子為a,2b的同構式(數學中把除了變量不同,而結構相同的兩個表達式稱為同構式.如果不等式兩側呈現同構特征,可將相同的結構構造為一個函數,進一步與函數的單調性取得聯系),進而將同構式視為函數f(x)=2x+log2x,而a,2b為該函數的兩個自變量,構造函數,通過研究其單調性比較自變量a與2b的大小.

數學同構式彰顯了數學的對稱和諧美,構造同構式的解題策略,培養了學生的抽象、轉化化歸等數學思維能力.

幫助學生學會用函數圖象和代數運算的方法研究這些函數的性質;理解這些函數中所蘊含的運算規律;運用這些函數建立模型,解決簡單的實際問題,體會這些函數在解決實際問題中的作用[1].

可以看出,只有將條件等式化歸為含有a與2b或a與b2的關系式,才能比較其大小關系.

3 創設科學情境,探求特殊點

例3(2020年高考數學全國新課標I 卷理科第20 題)已知A、B分別為橢圓E:+y2= 1(a ＞1)的左、右頂點,G為E的上頂點,= 8,P為直線x= 6 上的動點,PA與E的另一交點為C,PB與E的另一交點為D.

(1)求E的方程;

(2)證明: 直線CD過定點.

情境設計: 幾何畫板演示: 橢圓E:+y2=1(a ＞1)的左右頂點分別為A、B,P為直線l:x=t(t ＞a)上的動點,PA與E的另一交點為C,PB與E的另一交點為D,得直線CD.拖動點P沿直線l上下運動,讓同學們觀察動直線CD的運動特征.

問題1: (1)取a= 2,t= 4 時,請同學們觀察直線CD運動過程中有何發現?

(2)取a=3,t=3 時,請同學們觀察直線CD運動過程中有何發現?

(3)大家發現直線CD運動變化過程中的規律嗎?

投影例3(2020年高考數學全國新課標I 卷理科第20 題)

問題2: (1)能說出直線CD所經過定點的坐標嗎?

(2)你能先求出該定點的坐標嗎?

(3)已經知道直線CD所經過定點的坐標,要想證明直線CD過該定點,需要證明什么?

問題3: 同學們能歸納出一般性結論嗎? 試著證明一下.

設計意圖幾何畫板形象、動態、科學的演示試驗,讓同學們直觀觀察在橢圓變化、直線l左右運動、動點P上下運動的情況下,直線CD的“動中有定”的運動變化規律.

問題1 先觀察特殊再歸納一般, 借助幾何畫板中的橢圓、直線、點的可運動變化特性觀察特殊狀態和一般狀態: 當a= 2,t= 4 或a= 3,t= 3 時,拖動點P沿直線l上下運動,同學們可以直觀觀察出直線CD分別圍繞定點(1,0)或(3,0)旋轉運動.變換a、t的取值,通過(3)讓學生發現一般性規律: 動直線CD恒過定點應用幾何畫板不僅建立了形與數的聯系,同時體現由特殊到一般數學思想.

問題2(1)“說”出定點坐標,是將一般結論特殊化.既是問題1 的延伸,又是提醒“證明直線過定點”問題中的定點是可以預知的,為(2)作鋪墊.

求動直線經過的定點坐標方法有: 點斜式方程法、比較系數法、直線系法、特例驗證法等.(2)中的“先”意在引導同學們考慮特例驗證法,即在直線x=6 上取點P的兩個特殊位置,得到兩條直線,求其交點Q即可.多數同學可以聯想到利用特殊化思想,迅速求出定點坐標.

問題(3)綜合考查三點共線的證明方法: 定點Q坐標滿足直線CD的方程;直線CQ與直線DQ的斜率相等;直線CQ與直線DQ的方向向量共線.同學們可根據自己掌握知識情況進行選擇相應的方法,培養邏輯推理、數據處理、數學運算等數學核心素養.

問題2 呈現證明直線過定點時: 先特殊,后驗證一般的特殊與一般數學思想的應用.

問題3 以歸納法呈現特殊與一般數學思想的同時,重在引導學生對問題進行數學抽象,用數學語言表達問題、用數學方法構建模型解決問題的數學建模素養.

隨著《普通高中數學課程標準(2017 版)》的實施,基于數學學科核心素養的教學活動應該把握數學的本質,創設合適的教學情境、提出合適的數學問題,引發學生思考與交流,形成和發展數學學科核心素養.以上典例分別采用創設數學情境、現實情境、科學情境,并以“問題串”逐步引導學生分析問題、解決問題,建構特殊與一般數學思想,讓學生在熟悉、關聯、綜合的課堂情境中化一般為特殊、由特殊到一般,使問題化難為易、化繁為簡,收到良好的教學效果.

4 教學反思

題海戰術學習數學難以取得理想效果,學生提高數學解題能力和意識就要注重數學思想的領會和運用.如遇到一些較難問題,若從特殊情況進行分析,會使問題迎刃而解,特殊化思想往往孕育著一般問題的解決方法,因此,教師應將數學思想滲透貫穿于教學全過程,注重凝煉典型問題中的數學思想,強化應用意識,抓本質促能力.

用字母表示數、構造特殊函數等數學方法都是一般與特殊數學思想的產物,正確的數學思想指導有效的數學解題方法.

同時,《普通高中數學課程標準(2017 版) 》明確指出:“設計合適的教學情境,提出合適的數學問題是有挑戰性的,也為教師的實踐創新提供了平臺.教師應不斷學習、探索、研究、實踐,提升自身的數學素養,了解數學知識之間、數學與生活、數學與其他學科的聯系,開發出符合學生認知規律、有助于提升學生數學學科核心素養的優秀案例.”