2020年廣東省中考數學第22題解法評析與拓展研究

廣東省中山市第一中學(528400) 宋海培

2020年的廣東省中考已落下帷幕,各市的評卷工作也已完成.筆者參與了廣東省中考數學第22 題(圓的綜合題)的評卷工作,目睹了同學們五花八門的解答.經過評卷后的統計,本題平均分僅為2.8 分(滿分8 分),平均得分率為0.35,可見同學們的回答并不理想.這道題可以怎樣解? 這道題相關的圖形結構還有哪些可以總結的性質? 其他省市的數學中考對這些性質是否有過考查? 我們在教學中該怎么做? 這引起了我的很多思考,現整理出來,供大家參考.

1 原題呈現

如圖1,在四邊形ABCD中,AD//BC,∠DAB= 90°,AB是⊙O的直徑,CO平分∠BCD.

(1)求證: 直線CD與⊙O相切;

(2)如圖2,記(1)中的切點為E,P為優弧上一點,AD=1,BC=2,求tan ∠APE的值.

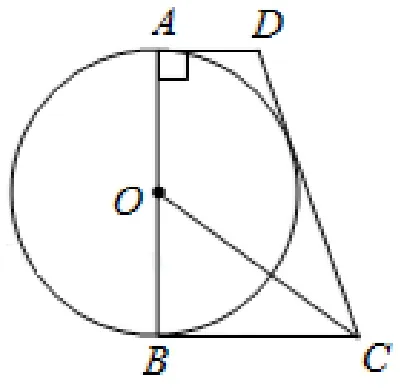
圖1

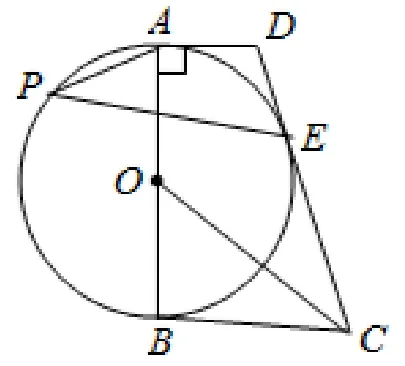
圖2

2 解法評析

(1)證明: 如圖3,過點O作OE⊥CD于點E.

∵AD//BC, ∠DAB=90°, ∴∠OBC= 180° -∠DAB= 90°, 即OB⊥BC.∵CO平分∠BCD,OE⊥CD,OB⊥BC, ∴OB=OE.∵AB是⊙O的直徑,∴OB是⊙O的半徑, ∴OE也是⊙O的半徑.∴直線CD與⊙O相切.

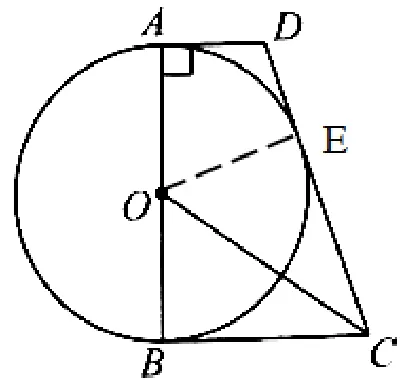
圖3

解法評析(1): ①,切線的判定通常認為有兩種常見題型及對應方法:本題的切線證明屬于“無交點: 作垂直,證半徑”這一類型,即⊙O與直線CD的公共點尚未明晰,所以可以采取先作垂線段OE,再證明這條垂線段的長度等于圓的半徑,從而證明直線CD是⊙O的切線;

②,利用角平分線性質證明線段相等,也可通過全等來證明;

③,說明垂線段OE等于半徑;

④,直線CD經過半徑外端且垂直于半徑,是圓的切線.

以上是本題的常規解法, 在評卷過程中發現了個別學生的其他解法, 同樣達到了證明切線的目的.如采用下面的思路: 在CD上截取CE=CB, 用SAS 證得ΔBCO∽= ΔECO, 進一步可同樣得到OE⊥CD以及OB=OE,所以直線CD與⊙O相切.

(2)解: 如圖4,連接OD,∵直線CD、AD、CB與⊙O相切, ∴AD=DE= 1,BC=CE= 2, ∠ADO= ∠EDO,∠BCO=∠ECO,∴∠AOD=∠EOD,CD= 3.∠AOD.∵AD//BC,∴∠ADE+∠BCE=180°,∴∠ODE+∠OCE= 90°, ∴∠DOC= 90°.∵OE⊥CD, ∠ODE=∠CDO,∴ΔODE∽ΔCDO,∴OD=∴在RtΔAOD中,OA=∴tan ∠AOD=

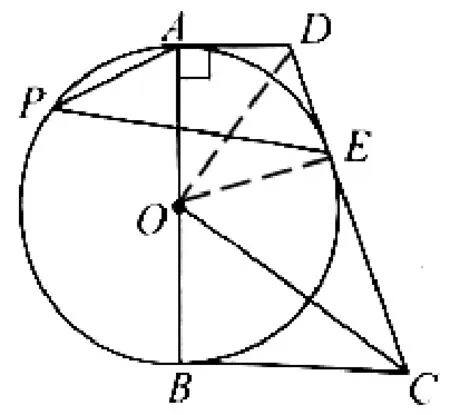
圖4

解法評析(2): ⑤,因為∠APE的三角函數不容易直接求得,進行角度的轉換是關鍵一步.此處的方法是結合圓周角定理和切線長定理將∠APE轉移至∠AOD,也可以轉移到其他角,如∠ABE.這決定了接下來的具體求解路徑,不同的解法亦可由此而發端.

⑥,運用切線長定理和相似等知識求得相關數據.此部分的具體求解方法也較多,相關的圖形性質很豐富,在后面詳細論述.

⑦,運用三角函數的定義和等量代換求得答案.

以上是第(2)題的一種解法(解法1),若將∠APE轉換為∠ABE,在ΔABE中進行求解也可,具體如下.

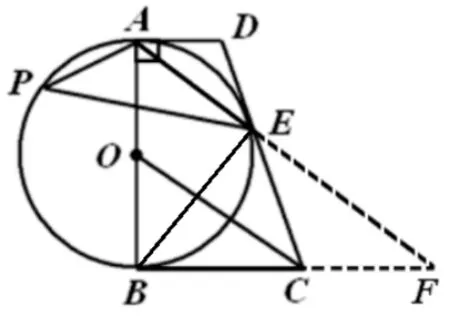
圖5

解法2: 如圖5, 連接BE, 延 長AE交BC延 長線于點F, 由得∠APE=∠ABE,∵AD//BC,∴∠DAE= ∠CFE, 易 得ΔADE∽ ΔFCE,AD=DE= 1,CE=BC= 2,根據射影定理有BE2=AE · EF, ∴tan ∠APE= tan ∠ABE=

解法2 不需具體求出半徑長,只需挖掘出AE與BE的關系即可,顯得更簡捷.這當然需要解題者有不斷總結反思從而形成的敏銳的解題感覺.解法2 在挖掘AE與BE的關系時用到射影定理這一基本圖形的相關知識.實際上,在前面的解法1 中,同樣可以運用射影定理獲得另外的解題路徑.

解法3: 如圖4,在RtΔCOD中由OE2=ED·EC求得OE=即OA=以下略.

本題還有其他解法, 如解法4: 作DH⊥BC, 得BH=AD= 1 =CH, 由勾股定理求得DH==AB, 故OA=(以下略).這是典型的梯形輔助線解法,也是一種比較容易想到的解法.

3 拓展研究

從以上解法評析可以看到,本題的圖形結構中蘊含了豐富的性質,值得進行研究和總結梳理,具體如下.

如圖6,已知AB是⊙O的直徑,AD和BC是⊙O的兩條切線,DC與⊙O相切于點E,連接BE、OC相交于點F,連接OD、AE相交于點H.圖中蘊含的豐富性質包括但不限于以下(證明不難,此處略):

圖6

(1)全等三角形有: ΔAOD∽= ΔEOD,ΔBOC∽= ΔEOC,ΔBCF∽= ΔECF,ΔADH∽= ΔEDH,ΔAOH∽= ΔEOH∽= ΔOEF∽= ΔOBF;

(2)相等的線段有:AD=DE,BC=EC,FB=FE=OH,AH=EH=OF,AO=EO=BO=r等;

(3) 具有2 倍關系的線段有:BE= 2OH(中位線) ,AE=2OF(中位線),AB=2OE(斜邊上中線)等;

(4) 角平分線有:OD平分∠ADC,OD平分∠AOE,OC平分∠BCD,OC平分∠BOE;

(5) 相等的角有: ①∠DAE= ∠AOD= ∠EOD=∠DEA=∠OEB=∠OCE=∠OCB=∠OBE,

②∠ODA= ∠ODE= ∠OAE= ∠OEA=∠COE=∠BOC=∠CEB=∠CBE,

③∠COD=∠AEB=∠AHO=∠BFO=90°等;

(6) 相似三角形有: ΔDAH∽ΔAOH∽ΔDOA∽ΔOCB∽ΔBCF∽ΔOBF∽ΔDCO∽ΔABE等;

(7)平行關系有:CO//AE,DO//BE,AD//BC等;

(8) 垂直關系有:OA ⊥ AD,OB ⊥ BC,OD ⊥AE,OC ⊥BE,OE ⊥CD,AE ⊥BE等;

(9)特殊四邊形有: 四邊形OFEH是矩形;

(10)重要線段關系還有:AD+BC=CD,AD·BC=OA2=OE2=ED·EC=r2,DO·BE=CO·AE=2r2.

4 他山之玉

當我們對以上圖形結構以及蘊含的圖形關系有深入的了解后,2020年廣東省中考數學第22 題以及許多類似的題目解決起來思路就可以開闊得多,達到“左右逢源”、“條條大路通羅馬”的境界.下面我們一起來欣賞其他省市對以上圖形結構的考查,這里只簡要列舉幾例.

1.(2018 大慶中考)如圖7,∠B= ∠C= 90°,M是BC的中點,DM平分∠ADC,且∠ADC=110°,則∠MAB=( ).

A.30°B.35°C.45°D.60°

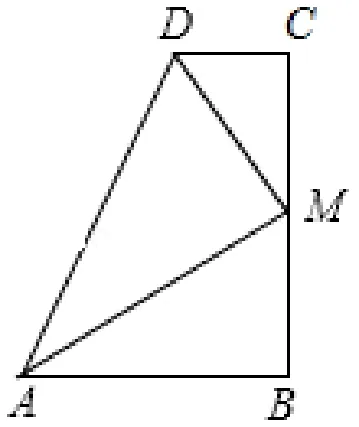
圖7

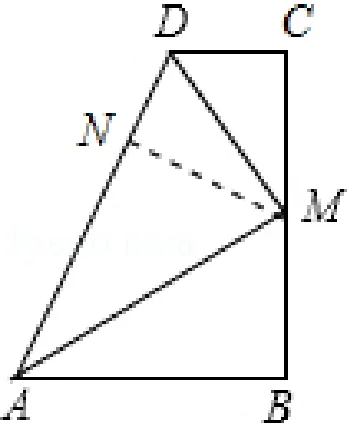
圖8

【分析】先根據平行線的性質求出∠DAB.如圖8,作MN⊥AD于N,結合角平分線的性質和判定求得∠MAB.

【簡評】若剔除圓的背景,2020年廣東省中考數學第22題實際上蘊含本題的結構.

2.(2019 武漢中考)已知AB是⊙O的直徑,AM和BN是⊙O的兩條切線,DC與⊙O相切于點E, 分別交AM、BN于D、C兩點.

(1)如圖9,求證:AB2=4AD·BC;

(2)如圖10,連接OE并延長交AM于點F,連接CF.若∠ADE=2∠OFC,DA=1,求圖中陰影部分的面積.

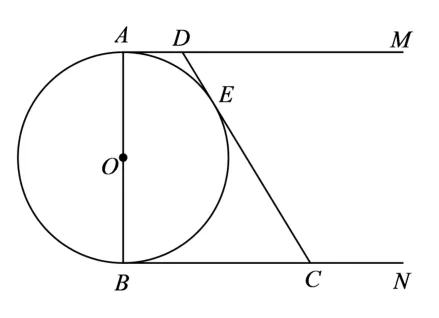
圖9

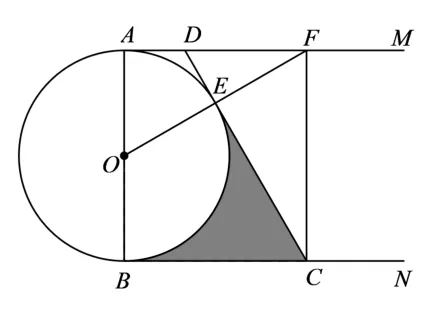
圖10

【分析】(1)如圖11,連接OD,OC,OE.∵AM,BN,CD是⊙O的切線,∴OA⊥AD,OB⊥BC,OE⊥CD,AD=DE,BC=EC, ∠ODE=∴AD//BC, ∠ODE+ ∠OCE=(∠ADC+∠BCD) =90°.∵∠ODE+ ∠DOE= 90°, ∴∠OCE= ∠DOE.又∵∠OED= ∠CEO= 90°, ∴ΔODE∽ΔCOE.OE2=ED · EC, ∴4OE2= 4ED · EC, ∴AB2=4AD·BC.

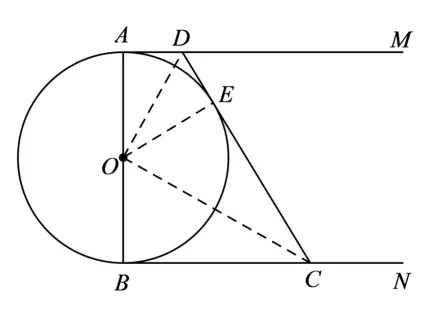
圖11

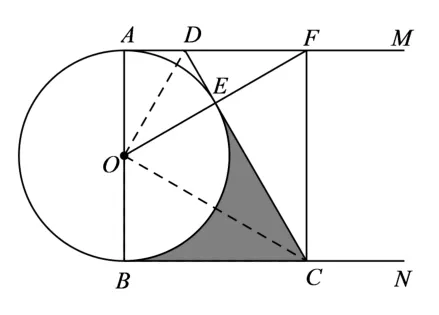
圖12

(2)解: 如圖12,由(1)知∠ADE=∠BOE,∵∠ADE=2∠OFC,∠BOE= 2∠COF,∴∠OFC= ∠COF,∴ΔCOF是等腰三角形.∵OE⊥CD,∴CD垂直平分OF.∴∠AOD=∠DOE= ∠OFD= 30°, ∠BOE= 120°.∴r=OA=BC=OB ·tan 60°= 3.∴陰影部分的面積S=

【簡評】本題較充分地展示了前面總結的圖形性質的運用.

3.(2016 鄂州中考) 如圖13 所示,AB是⊙O的直徑,AM和BN是⊙O的兩條切線,DC與⊙O相切于點E,連接OD、OC、BE、AE,BE與OC相交于點P,AE與OD相交于點Q,已知AD=4,BC=9.以下結論:

①⊙O的半徑為②DO//BE, ③PB=④tan ∠CEP=

其中正確的結論有( )

A.1 個 B.2 個 C.3 個 D.4 個

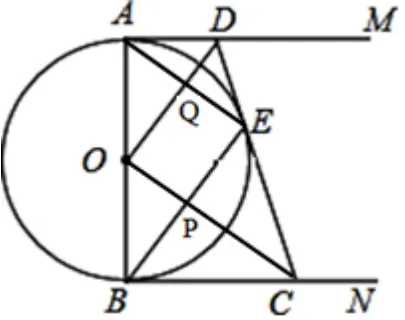
圖13

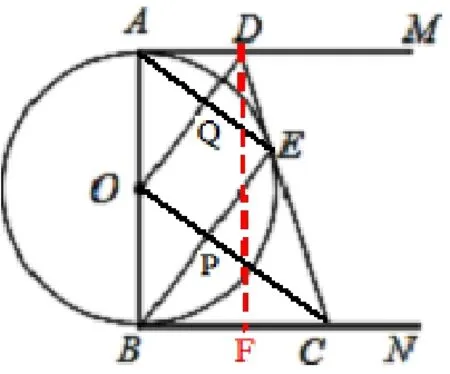
圖14

【分析】 ①如圖14,過點D作DF⊥BC于點F,∵AM和BN是⊙O的兩條切線, ∴AB⊥AD,AB⊥BC, ∴四邊形ABFD是矩形, ∴AD=FB,AB=FD, 又∵AD= 4,BC=9,∴FC=9-4=5,∵AM,BN,CD是⊙O的切線,∴AD=DE,BC=EC,∴DC= 9+4 = 13,在RtΔDFC中,DC2=DF2+FC2, ∴DF== 12,∴AB=FD=12,∴⊙O的半徑是6.故①錯誤;

②如圖15, 連接OE,∵AD,ED是⊙O的切線,∴AD=DE, ∠OAD=∠DEO= 90°, 又∵OD=OD,∴ΔAOD∽= ΔEOD,∴∠AOD= ∠EOD=∴∠AOD= ∠ABE,∴DO//BE.故②正確;

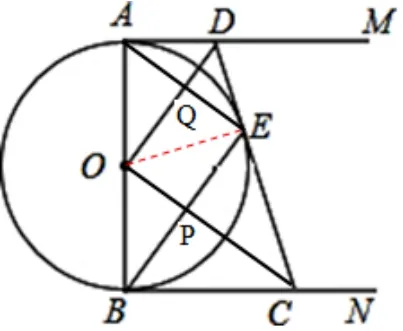
圖15

③根據勾股定理得,OC=由①知OB= 6, 易知ΔOPB∽ΔOBC, 則∴PB=故③正確;

④易知∠CEP ＞∠ECP, 所以CP ＞ EP, 故tan ∠CEP ＞1,故tan ∠CEP=錯誤.

綜上,正確的答案為: B.

【簡評】本題充分展示了本文所探討的這個典型圖形的性質.熟練使用前面總結出的方法和結論,不難快速解出此題.

5 教學啟示

最近八年(2013年到2020年),廣東省中考數學試卷的幾何綜合題都是用圓的綜合題來把關考查學生的推理素養.這些圓的綜合題雖然千變萬化,但是善于總結基本圖形、具有較高推理素養的學生就能很好地解決.

基本圖形具有典型性和生長性.教材中的基本概念、基本方法、基本原理對應的圖形還有一些典型的例題與習題都是基本圖形(典型圖形)的重要來源.如本文重點分析的2020年廣東省中考數學第22 題第(1)小題實際上與人教版九上教材第98 頁中的例1 大同小異(類型相同,方法相通,形式有異).另外人教版九上教材第102 頁習題中的第11 題,第125 頁復習題中的第15 題均有與本題高度相似的圖形結構.如果平時做好相關的訓練以及注意解題后的總結,這道廣東省的中考題是不難攻克的.

引導學生分析和總結基本圖形(典型圖形)是提高推理素養的重要途徑.我們在教學中應該加強引導學生對基本圖形的研究和整理歸納,在分析和總結基本圖形的過程中不斷落實基礎知識、夯實基本技能,積累基本活動經驗、感悟數學基本思想,從而切實提高分析問題、解決問題的能力,提高推理素養.