走向培育核心素養的深度教學
——以“圖形變化規律中考復習”教學為例

廣東省東莞市長安實驗中學(523850) 蔡映紅

“多”和“快”是工業經濟時代教育的要求,而現代社會是一個飛速發展的知識經濟時代,所需要的人才是有創新能力、能解決復雜問題的人,靠“多”和“快”是難以培養的,這就要求我們不得不轉變人才培養方式.課程改革指向核心素養的培育,是時代和經濟社會發展的必然趨勢.作為一名教師,我們的根本任務是立德樹人,以學科核心素養為教學的出發點,通過教學改進培養學生的價值觀、必備品格與關鍵能力.在當前深化課程改革的大勢之下,“百度一下就知道”的教學必須改變,促進學生“深度學習”順勢而生.而要幫助學生學會“深度學習”,這要求教師能開展“深度教學”.

1 深度教學

深度教學的“深度”,指向在引領學生“理解”與“創新”上.深度教學的目的,不是要培養只知“守成”的“工匠”,而是要培養“有創造力”的人才,即其根本指向人的全面發展,是培養學生核心素養的基本路徑.“教”不等于“學”,深度教學必須建立在促進學生深度學習的基礎上.深度教學的表現形式也許會有千萬種,但其共性特征如下: (1)不是一般的學習者的自學,它需要教師的引導; (2)不是表層的學習,而是在已有認知成果下有新的收獲;(3)是學習者感知、思維、情感、價值觀的全面投入的活動過程;(4)能培養學生核心素養.

深度教學的目的是為了促進學生深度學習,體現了育人為本的理念,讓每個學生能發現自己的潛能,有持久的學習興趣.那么,如何開展深度教學? 下面,筆者以“圖形變化規律中考專題復習”課的教學實踐為例,談談走向培養核心素養的深度教學設計的幾點思考.

2 走向培育核心素養之深度教學設計

在“圖形變化規律中考專題復習”的備考中,我們發現:對中下層學生而言, 能較好解決一些簡單的數式變化規律,但對于較復雜的圖形變化規律,往往束手無策.老師講個好幾遍,學生還是錯.究其本質,就是學生對所學內容不理解、記不住,或者記住了但無法遷移解決相關新問題,還有就是沒興趣、不愛學.而這些問題不是靠多做幾次就能解決的.為此,筆者嘗試開展深度教學.以探究學習的專題形式來設計,旨在通過開放式的探究活動,問題引導,幫助學生自主梳理,交流, 反思, 獲得深刻認知, 形成學生自我內在的經驗積累,獲得研究圖形變化規律的一般思路,實現優化解題方式,促進學生數學核心素養的進階發展.

2.1 內容和內容解析

2.1.1 內容

圖形變化規律的探尋問題.

2.1.2 內容解析

規律探尋問題,就形式而言,有數式變化規律、圖形變化規律和循環排列變化規律等等.圖形變化規律,往往與三角形性質、勾股定理、銳角三角函數、相似三角形、一次函數、反比例函數等知識融合在一起,靈活多變.圖形變化規律的探尋,學生不僅需要經歷觀察、分析、比較、聯想、猜想、歸納、驗證等一系列探究與推理過程,而且需要具備化歸思想、函數思想、數形結合思想、建模思想、幾何直觀和空間想象能力.基于以上分析,可以確定本節課的教學重點: 探尋圖形規律的一般思路和通法.

2.2 目標和目標解析

2.2.1 目標

(1)復習探尋數式變化規律的一般思路和通法,從中體會化歸思想和函數思想.

(2)在具體的問題情景中,探尋圖形變化規律的一般思路,從中體會化歸思想、函數思想和數形結合思想.

2.2.2 目標解析

達成目標(1)的標志是: 掌握常見數式規律的結構特征和尋找規律的通法;

達成目標(2)的標志是: 能將圖形變化規律的探尋思路轉化為數式規律的探尋,達到“以不變應萬變”.

2.3 教學問題診斷

2.3.1 教學問題分析

圖形變化規律的探尋,之所以比數式變化規律的難,主要體現在它的綜合性強,往往與幾何、函數等知識融合在一起,靈活多變.因此,本節課的教學難點: 如何將探尋圖形規律轉化為探尋數式規律.

2.3.2 深度教學策略

為突破此難點, 本設計以數式變化規律的通法為輔題,在引領學生經歷探尋圖形變化規律的過程中體驗兩種方法:拆圖法(需較強的幾何直觀能力)和函數法(將圖形變化規律問題轉化為數式規律問題,雖存在一定計算量,但多數學生掌握較好).

2.4 教學設計流程

2.4.1 溫故知新,夯實當前發展區

問題1: (2019·銅仁)按一定規律排列的一列數依次為:按此規律排列下去,這列數中的第n個數是_____(n為正整數).

教學說明: 學生對“尋找規律”的當前發展區的特點是尋找數式規律的能力較好,而尋找圖形規律的能力較弱,因此本節課從“穩固地基”入手,以一道呈現三種變化形式的數式規律展開教學.此題有三種規律形式: (1)符號規律;(2)分子的指數呈等差數列;(3)分母呈“差后等差”數列(即等差數列前n項的和).它是研究圖形規律作輔墊的輔例題.

2.4.2 通法梳理,構建研究思路圖

問題2: 研究數式規律的一般思路是怎樣的? 初中階段常見的數式規律有哪些?

問題3: 用思維導圖梳理尋找數式規律的研究思路、結構特征、解決問題的通法等.圖1 為學生集團隊力量,最終構建的思維導圖.

圖1

教學說明: 此問題的提出,在于引導學生有方向的思考,提煉數式規律的“研究套路”,掌握常見數式規律的結構特征與解決問題的通法.此過程,是一個生生交流、教師適當引導的過程,學生將個性思考與他人思考融合,構建知識體系,形成個性化研究思路圖譜.此環節為學生提供了相互交流、自我歸納與表達的平臺,也為以后的知識梳理提供范式,讓學生逐步學會圖式整理的數學思維習慣,達到培養核心素養的目的.

2.4.3 例題教學,辨析中本質內化

某些地域范圍內的鄉土建筑總能呈現出相近的類型特征，而這種特征就成為不同鄉土建筑類型劃分的重要依據。我們可以借鑒符號學及語言學的方法，以“適切項”為條件，盡量選取獨特性較強的區域范圍作為基本型(即本文所說的“原”)，進而劃分不同的源頭。在選擇中，大范圍根據影響建筑最深的“地盤”（平面）、“側樣”、“正樣”（剖面），并結合具體的用尺、營造細部特色——“細樣”或“小樣”，加以甄別 [8]。

例1(2016·重慶)如圖2,下列圖形都是由同樣大小的小圓圈按一定規律所組成的,其中第①個圖形中一共有4 個小圓圈,第②個圖形中一共有10 個小圓圈,第③個圖形中一共有19 個小圓圈, …,按此規律排列,則第⑦個圖形中小圓圈的個數為( )

圖2

A.64 B.77 C.80 D.85

參考答案: D

解析1(拆圖法):

解: 觀察圖形特點,可將圖形分為兩部分: 上面的三角形和下面的正方形.得到小圓圈的個數分別是:

第①個圖形: 3+12=(1+2)+12=4;

第②個圖形: 6+22=(1+2+3)+22=10;

第④個圖形: 15+42=(1+2+3+4+5)+42=31;

…所以第n個圖形: (1+2+3+···+n+1)+n2.

當n=7 時,小圓圈個數=(1+2+3+···+8)+72=85.

故選D.

解析2(函數法):

解: 通過計算,得到小圓圈的個數分別是(圖3):

圖3

依據“差后等差”特征可得, 序號n與數列中的相應數y成二次函數, 因此可設y=an2+bn+c(a /= 0),把(1,4),(2,10),(3,19) 代入, 得解得故y= 1.5n2+1.5n+1,所以第n個圖形:1.5n2+1.5n+1.當n=7 時,1.5×72+1.5×7+1=85.

故選D.

教學說明: 本例題教學的目的是“圖”轉“數”的本質內化過程.把握本質的過程,是去除非本質屬性的干擾、辨析出本質屬性與非要質屬性的區別的過程,也是對教學內容深度開發的過程.這個過程,不是教師將解法一一告知學生,而是給學生搭建交流分享平臺,在“提問”、“探究”、“質疑”、“辨析”、“歸納”等等中剝絲抽繭,讓思維靈動.此圖形變化規律的探尋,方法一是運用幾何直觀,用“拆圖法”從圖形結構中直接尋找規律.這種方法對學生的觀察角度要求較高,利于培養幾何思維能力與邏輯推理能力.我班只有大約26%-30%的學生能做到,方法二是通過一定的計算,運用函數思想,將探尋圖形變化規律轉化為探尋數式變化規律, 這種“圖”轉“數”的本質內化的方法能幫助更多的學生獲得成功的體驗,我班有73%-80%的學生能做到.它更適合做為通法來理解.

2.4.4 拓展遷移,體驗中本質外化

例2(2018·廣東)如圖4,已知等邊ΔOA1B1,頂點A1在雙曲線y=(x ＞0)上,點B1的坐標為(2,0).過B1作B1A2//OA1交雙曲線于點A2, 過A2作A2B2//A1B1交x軸于點B2, 得到第二個等邊ΔB1A2B2; 過B2作B2A3//B1A2交雙曲線于點A3,過A3作A3B3//A2B2交x軸于點B3,得到第三個等邊ΔB2A3B3;以此類推, …,則點B6的坐標為____

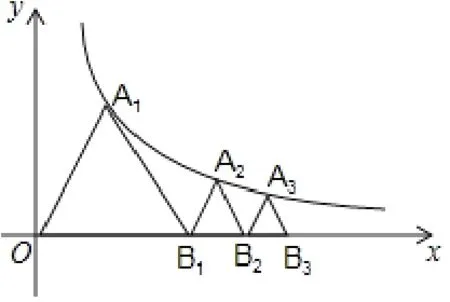
圖4

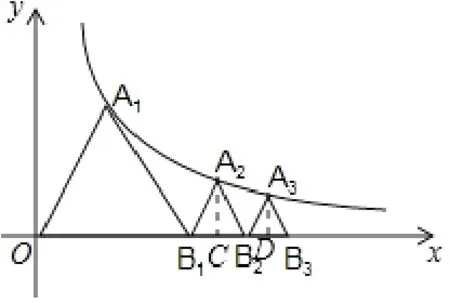
圖5

解析: 此題無法運用“拆圖法”,必須通過計算來探尋規律.根據等邊三角形的性質以及反比例函數圖象上點的坐標特征分別求出B2、B3、B4的坐標,得出規律,進而求出點B6坐標.

解: 如圖5, 作A2C ⊥x軸于點C, 設B1C=a, 則∵點A2在雙曲線解得-1,或a=-1(舍去),∴OB2=OB1+∴點B2的坐標為作A3D ⊥x軸于點D, 設B2D=b, 則A3D=OD=OB2+B2D=∵點A3在雙曲線y=解得b=或b=∴OB3=OB2+2B2D=∴點B3的坐標為同理可得點B4的坐標為即(4,0);…,∴點Bn的坐標為∴點B6的坐標為故答案為

教學說明: 本環節的目的是解決知識向學生個體經驗的轉化,強調學生對上一環節學習結果“圖”轉“數”的外化.此圖形變化規律的探尋,無法運用幾何直觀,用“拆圖法”從圖形結構中直接尋找規律.只能通過一定的計算,運用函數思想,將探尋圖形變化規律轉化為探尋數式變化規律.從而體現函數法做為規律探尋的通法地位.

2.4.5 畫龍點睛,凝練中素養進階

問題4: 研究圖形變化規律的一般思路是怎樣的? 通法是什么?

學生自主合作完成,展示成果(圖6):

圖6

教學說明: 本環節讓學生自主合作完成,展示成果.滲透化歸思想,理解本質,形成關于圖形變化規律問題的頂層理解: 若從直觀幾何中無法解決,可以嘗試計算前幾個圖形相關量的變化結果,轉化為“數式規律”的研究,我們有信心解決此類相關問題.

3 開展培育核心素養的深度教學的思考

3.1 用聯系的觀點指導教學

“聯系的觀點”是國際數學教育界的一個普遍趨勢.它既與“理解教學”有直接的聯系,又能讓我們從更廣泛的角度進行有邏輯的思考分析,獲得更大的認識深度.如本節課第一、三、四環節的設計立足于新舊知識間的聯系,第二、五環節的設計在于構建知識體系間的結構聯系.用聯系的觀點利于從全局觀的角度指導教學,顯現認知的發展,用發展代替重復.

3.2 用好的問題鏈引領教學

深度教學離不開教師的適當引領,好的問題引領能引領學生從知識層面、技術層面的思考深入到思維層面的思考.在教學過程中,教師應依據預設與實際學情做出“追問”、“反問”等持續性的引導,“讓思維在‘問題鏈’中‘淺入深出’”(吳正憲語).促進學生深度學習,從而提煉核心問題.

3.3 要有充分的交流與互動

充分的交流與互動,利于學生學會反思,學會優化,學會合作,這是核心素養的體現之一.合理留白課堂時間,讓學生展學展講.生生間、師生間有足夠的時間思維碰撞,相互補充,相互啟發,從而推進知識的整合與內化,又利于學生逐步學會邏輯思考,形成理性精神.

4 結束語

現代社會技術迭代快速, 學生的學習也從原本的以記憶、模仿、訓練為主的輸入式學習,轉變為以體驗、理解、遷移為主的深度學習.我們不是要培養能“考高分”的學生,而是要培養有“創造力”的人才.這要求教師能夠直面改革,主動學習,具備能開展深度教學的素養.