核心素養下初中數學對學生建模能力培養實踐探索

陳雅君

摘? 要：數學核心素養包括數學建模、數學運算、直觀想象以及數據分析等內容，其中數學建模乃是核心素養的主要內容之一，是初中數學教學非常重要的任務，也是提高學生分析問題能力、解決問題能力，培養學生數學知識應用意識的重要內容。在新課改要求下，廣大數學教師當重視學生建模能力培養。本文立足于初中數學教學和核心素養兩個維度，重點探討初中數學教學中學生建模能力培養的有效策略。

關鍵詞：初中數學;模型思想;數學建模;建模能力;核心素養

中圖分類號：G633.6? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DOI：10.12296/j.2096-3475.2021.07.265

一切數學知識其實都來源生活，都能夠在生活中找到實際模型。而數學模型思想就是通過建立數學模型來解決實際問題。這也就要求廣大數學教師在教學實踐中要教會學生建立數學模型，注重培養學生建模能力，給予學生機會，讓學生自主參與、體驗模型建立過程，通過模型解決問題，不斷獲得思維能力的發展。本文主要以北師大八年級教學內容為例，結合生活中的“一次模型”這一教學內容探討培養學生建模能力的有效策略。

一、創設數學情境，引導學生感知模型思想

要想培養學生建模能力，首先學生應該了解模型思想，具備初步感知模型思想的能力。為此，我們在初中數學教學實踐中，不僅要指導學生掌握數學公式、符號、方程、圖形、計算方法等內容，同時也要引導學生建立知識間的聯系，家里數學知識與生活的聯系。創設情境無疑是最佳選擇。通過創設與生活接近的模型或者情境，讓學生快速建立數學知識與知識間、數學知識與生活間的聯系，提高學生數學感知能力。例如，生活中的“一次模型”這一內容教學中，數學教師可以引導學生回顧知識，建立聯系。首先給學生舉例一元一次方程（組）、一次函數、一元一次不等式（組），請學生回憶這些知識，結合已有經驗談一談這些知識之間有什么樣的關系？其次引導學生舉例說明生活中常見的用一元一次方程（組）或一次函數或一元一次不等式（組）相關知識解決實際問題。以問題求解過程深化學生對三者之間關系的理解，為后續指導學生建立數學模型奠定基礎。

二、開展探究活動，鼓勵學生主動建立數學模型

真正有效率、有價值的學習不是掌握幾個數學概念、定理公式，或者計算幾道題。而是深入思考數學概念是如何形成的？數學定理和公式如何推導出來的？這樣的學習過程自然離不開探究活動。通過開展探究活動，能夠最大限度地給予學生參與數學活動的權利，學生能夠在課堂上參與、體驗、感悟數學知識產生、發展的過程，從而自主建立起能夠理解的數學模型。

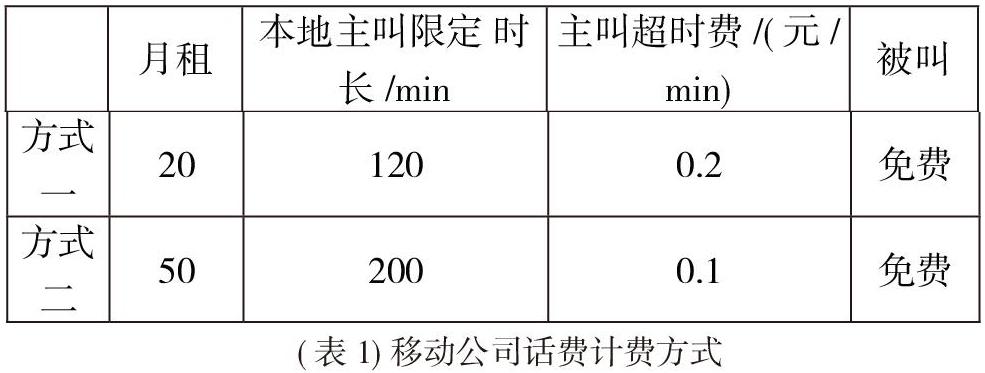
同樣在指導學生學習生活中的“一次模型”時，開展小組探究活動，給學生提供相應的學習材料，提出學習任務，引導學生小組交流討論，提出解決問題的方案。比如，材料1：探索出租車如何計價？要求學生小組交流討論，解決如下問題：①日間出租車價與里程數之間的函數關系？②夜間出租車價與里程數之間的函數關系？③當遇到紅燈或堵車時的計價情況？材料2：教育開銷的調查，學習任務：①試估算自己從學習到大學畢業前總共需要多少教育資金？②結合這些費用，幫自己父母制定一個儲蓄計劃？③用不等式表示各種儲蓄渠道所能儲存錢的最低數量。材料：話費設計，給學生提供一張單月話費清單和移動公司話費計費方式，如下表1.要求學生結合自己所學的一元一次方程、一元一次不等式或一次函數等知識，構建相應的數學模型，設計出最合理的話費方案。

結合學生的認知水平、學習能力設計符合學生發展需要的探究學習活動，引導學生運用所學的方程、函數、不等式等數學知識主動建構數學模型，讓不同認知水平、不同學習層次的學生都能夠經歷“問題情境—建立模型—求解—解釋與應用”這一知識探究過程，在學生感知數學模型的基礎上鼓勵學生嘗試自主建立模型，逐步提高學生數學建模能力。當然，如果考慮不同層次學生解決問題能力不同，在這一內容教學中，數學教師還應當盡量給學生設置不同情境，提供具有層次性的學習材料，由易到難、循序漸進地讓學生建模解決問題，讓不同層次的學生在數學上得到不同的發展。

三、增設課堂練習，幫助學生掌握數學模型思想

模型思想的難點在于建模，但目標指向運用。感知模型思想→建立模型→運用模型，經歷過程才是真正掌握模型思想。所以，在指導學生建模后，我們還應該給予學生實踐的機會，讓學生將掌握的數學學習方法運用于解決實際問題中去，通過反復練習驗證模型思想，運用模型解決問題。且反復練習也是提高學生解決問題能力，幫助學生鞏固提升的重要過程，是模型思想得以應用不可或缺的一部分。

教學完上述內容后，不妨給學生提供一個練手的機會，設計一個“練習提供，鞏固運用”環節，出示練習題：已知y1=-x+3，y2=3x-4，當x取何值時，y1>y2？你是怎樣做的？小組互相交流并自主解答。學生通過畫圖解決問題，在自主學習中進一步體驗一元一次不等式與一次函數的圖象之間的結合是解決此類問題核心所在，深化學生對知識的理解，讓學生真正意識到數學知識間的關系，意識到建模的重要性，從而在后續問題解決中主動運用模型思想、建立數學模型，巧妙地化解數學難題，快速解決一般數學問題，提高學生建模能力和解決問題的能力。

四 、結語

綜上所述，學習知識的最終目的是運用知識解決問題，而解決但部分數學相關問題都涉及到不同數學模型。廣大數學教師當重視學生建模能力培養，讓學生真正感知數學模型，主動建立數學模型，應用數學模型，提高學生解決問題能力，促進學生核心素養發展。

參考文獻：

[1]藏武存.試論初中數學教學中如何培養學生的數學建模能力[J].科學咨詢（科技·管理），2018（08）：121.

[2]崔德.芻議“建模思想”在初中數學教學中的應用[J].中學數學，2018（12）：65-66.

[3]郭川瑜.論初中生數學建模思想的培養[J].西部素質教育，2016，2（17）：106.

（河北省張家口市第二十中學? 河北張家口? 075000）