在強化教材分析的基礎上優化教學設計

【摘 要】教學內容分析的基本點通常有內容的現實與文化背景、表征方式、探索路徑等，通過對教材內容的多角度分析，可以設計出自然地發現與提出問題、自然地發現解決問題思路的思維過程，從而進一步啟迪我們設計出符合數學本質和認知規律的教學過程。

【關鍵詞】教材分析;教學設計;問題情境;數學審美

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2021）20-0029-04

【作者簡介】石志群，江蘇省泰州市教育局（江蘇泰州，225300）教研室主任，正高級教師，江蘇省特級教師。

發展學生數學核心素養是2017年版高中數學課程標準提出的要求，而數學基礎知識因其經典性、基礎性成為實現這一目標的重要載體。筆者認為，對教材中的基本內容進行強化分析、深化認識、把握本質是提高教學設計水平，發展學生數學素養的根本途徑。本文以“等差數列前n項和”為例對此作初步探索。

一、內容基本點分析

筆者先對本節內容的三個基本點作梳理。

1.問題情境。

等差數列的問題情境通常有兩類：現實情境和文化情境。

問題的現實情境較多，常見的有：

①花壇有若干層，各層花盆數依次成等差數列，求花壇上花盆總數（類似的，貨架上貨物總數的計算，求一堆鋼管總數等）;

②單利存款，本利總和;

③從材料工地運送電線桿到500米以外的公路的同一旁埋設，每隔50米在路邊埋一根。已知每次只能運3根，要完成運24根電線桿的任務，并返回材料工地，問運輸車的行程是多少米？

文化情境有：

①畢達哥拉斯學派的“三角形數”;

②高斯的故事;

③中國古代的“垛積術”（高階等差數列求和）中最基礎的數列——等差數列。

創設的問題情境既要能提出本節課要研究的問題，又要能與推導方法產生思維的鏈接，還要盡量避免過分的 “啟發”，否則使學生由情境本身直接知曉推導方法，會掩蓋思維的過程。當然，情境不宜復雜，以免沖淡主題，加大學習難度，要以簡單而蘊含本質的情境引入，促使學生比較容易地提出本節課的研究問題（主題）。換言之，情境的創設要力求入口淺、寓意深。

2.等差數列的表征方式。

數學對象的表征方式對數學思維活動起著一定的啟發、誘導作用，善于運用不同方式對數學對象進行表征，并由表征方式產生聯想是一種重要的數學素養。

等差數列是一種基礎的、重要的數列模型，從數學史看，其表征方式主要有——

（1）定義表征：an-an-1=d（n∈N*，n≥2）。

（2）代數表征：通項公式an=a1+（n-1）d，或函數形式an=an+b。

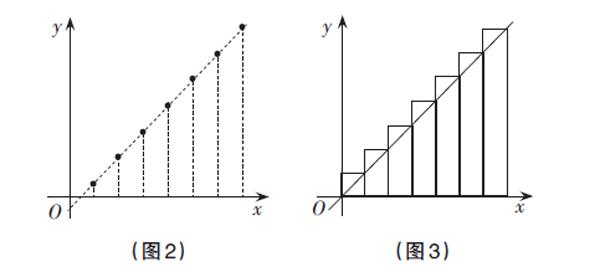
（3）幾何表征有3種：形數表征，如三角形數、四邊形數等（見圖1）;圖象表征，即一次函數中自變量取正整數的點列（見圖2）;面積表征，即分別以公差d為底邊（在x軸上），以an為另一條邊（有向線段）構成的系列矩形（見圖3）。

[（圖3）][（圖2）][O][x][y] [O][x][y]

3.探索路徑。

基于等差數列的代數和幾何表征，可得到兩種探索等差數列前n項和的思路。

（1）代數表征下的思路。由配對法，將所對應的式子保持其“結構”。對于1+2+3+4+…+100而言，1+2+3+4+…+100=（1+100）×[1002];對于首項為a1，公差為d的等差數列{an}，當n為偶數時，Sn=a1+a2+…+an-1+an=（a1+an）+（a2+an-1）+…+（a[n2]+a[n2]+1）=（a1+an）[n2];當n為奇數時，Sn=a1+a2+…+an-1+an=（a1+an）+（a2+an-1）+…+（a[n-12]+a[n+32]）+a[n+12]=（a1+an）[n-12] + [a1+an2] = （a1+an）[n2] 。

無論n是奇數還是偶數，等式的形式是一樣的，我們得到了等差數列的前n項和為Sn= （a1+an）[n2] 。

以上思路還是比較自然的，難點是如何自然地鏈接到本節課的核心內容——“倒排相加法”。關于這一點，可從幾何表征的思路中獲得啟發。

（2）幾何表征下的思路。對于圖1，就是求圖中點的總數。在此處可以引導學生聯想幾何中是如何求三角形的面積的。于是“補形”的思路就自然出現了（即用一個全等的三角形“倒扣”上去，補成一個平行四邊形，圖略）。

與此類似地處理圖2、圖3，將不“規則”的圖形補成規則的圖形，將未解決的圖形補成已經解決了的圖形。這里的“補形”體現的就是“倒排相加”的思想，將變化著的項的求和轉化為常數列的求和。因此，只要將圖形意義用代數符號表示出來，就能自然地得到倒排相加法。

如何解決代數表征下引導學生自然地想到倒排相加的方法呢？

比較簡便的方式就是“數形聯想”：Sn= （a1+an）[n2]的幾何意義（或幾何表征）是什么？也就是引導學生思考：這個公式使我們想到了什么？很顯然，這是梯形面積公式的結構形式，于是，將梯形補成平行四邊形的思路自然就產生了。

此外，還可以從數學審美的角度反思求1+2+3+…+100的過程，配對法的思維過程是：

首項與末項的和：1+100=101

第2項與倒數第2項的和：2+99=101

第3項與倒數第3項的和：3+98=101

……

第50項與倒數第50項的和：50+51=101

所以，S100=（1+100）×[1002]=5050。

如果用于求1+2+3+…+100+101的值，就會“多”出一項“51”沒有與之相配的項，而相同的問題卻用不同方法，顯得不夠“美”，怎樣才能美呢？完整是美、一致是美、對稱是美，于是，我們就要反思：在和式中的項的地位是一樣的，為什么配對時到了“50”就停了？這個“工作”應該繼續下去：

1 + 100 = 101

2 + 99? = 101

3 + 98? = 101

……

50 + 51 = 101

51 + 50 = 101

……

100 +? 1 = 101

這樣，兩個公差互為相反數的等差數列躍然紙上，而且無論n取奇數還是偶數，方法就統一了。這個方法不僅適用于特殊的等差數列，而且適用于一般的等差數列。

二、教學思考

1.數列研究的核心問題是什么？

從各種教科書上可以看到，數列（包括各種特殊的數列），其研究的內容主要是通項公式、性質及若干項的和。這說明，“和”是數列這一數學分支的主要研究問題之一;同時也說明，“通項”與“和”是其核心問題（性質即為“項”與“和”及其之間具體的特性及關系）。關于“和”，一方面其在現實中有廣泛的應用（商場中的貨架上堆放的商品總數、銀行存款中的若干模型等），另一方面函數的級數表示正是數列和的形式，它體現了人們認識變化世界的觀念和方法的巨大進步，也是數學應用于現實的重要途徑。

總之，“和”應該是數列研究的核心問題之一。

2.為什么求等差數列前n項和可用倒排相加的方法？怎么想到倒排相加的方法的？

在教學中不能用高斯的思考結果替代學生的探究性思維;不能用鋼管堆的原型作為初始問題，立即給出倒排相加的思路，否則就掩蓋了問題的抽象過程，對思路作出了過度的告知。

事實上，我們非常重視幾何中的“割補”方法，經常運用這種方法將不規則的形、體轉化為規則的形、體，將不熟悉的形、體轉化為熟悉的形、體，但我們忽視了其與代數中的類似的數學技巧的溝通與聯系。在代數中我們也常通過配湊、添減等技術處理代數式，進行問題的轉化，這與幾何中的“割補”法在思想上是一致的。有了這種認識，解決上面的“為什么”“怎么想到的”等問題就比較容易了，因為這種思想方法在幾何中已經有了應用，幾何的直觀也更易于為學生所理解。

3.等差數列的基本特征是什么？

從形的角度看，等差數列具有以下基本特征：第一，項具有線性關系，其圖象在一條直線上;第二，均勻分布，項所對應的點均勻分布在一條直線上。在幾何上，這種分布的n個散點（k，ak）（k=1，2，…，n）的“中心”為（[1+n2]， s）;從物理上看，這n個點的“重心”為（[1+n2]， s）。由圖形的幾何性質，或由物理圖形重心的概念都可以知道， s就是點A1（1，a1）與點An（n，an）的連線中點的縱坐標，即[a1+an2]。

從數的角度看，等差數列的“逆序”排列所得數列仍是一個等差數列，即若等差數列a1，a2，…，an的公差為d，則有數列an，an-1，…，a2，a1是公差為-d的等差數列，即有Sn= a1+a2+a3+…+an=a1+（a1+d）+（a1+2d）+…+[a1+（n-1）d]且Sn=an+an-1+an-2+…+a1=an+（an-d）+（an-2d）+…+[an-（n-1）d]。由此也容易發現兩個式子相加的思路。

4.“倒排”相“拼”的本質是什么？

我們知道，平行四邊形的面積公式是基于“祖暅原理”的，即“用平行于底邊的直線截，所截得的線段均相等”。而圖1這樣的等差數列幾何表征，拼出來的四邊形也具有類似的特性：每一行中點的個數都是相同的。因而，通過“拼湊”，使得“變”變為“定” （將一般的等差數列轉化為特殊的等差數列——常數列），便是“倒排”相“拼”的本質。

三、教學設計建議

基于上述分析可以發現，等差數列求和公式既有著廣泛的應用價值，也有著深刻的數學背景，還蘊含豐富的文化內涵，合理地進行教學設計，可以增強學生的數學應用意識，發展理性思維，培養關鍵能力，提升數學素養。

筆者建議，可以用含實際背景的問題情境進行引入，提出本節課的核心問題：等差數列前n項和如何求？可以是具體的等差數列，也可以是一般的等差數列。如果是后者，學生容易由通項公式轉化為前n個自然數的和。

如果學生想到高斯用配對法求和的思路，可以先重復一下求和過程，再研究一般的問題。這樣學生自然會想到分成偶數個項與奇數個項進行討論。

解決問題后，再追問：高斯是怎么想到這個思路的？你根據S100=（1+100）×[1002]的推導過程有何發現？甚至可以追問：這個式子的幾何意義是什么？進而使學生想到：一是將一般的等差數列轉化為常數列，二是梯形的面積公式。

接著再從數學審美的視角反思配對法，提出問題：為何同一問題卻用不同的方法解決？追求統一是數學的基本價值要求，應該找到不分項數是偶數還是奇數的一致方法;引導學生對和式中的各項地位均等進行認識，想到將“配對”的工作繼續進行下去的思路，從而發現倒排相加的思路。

在從代數表征的視角解決問題后，再提出問題：數學對象通常可從“數”與“形”兩個形式進行表征，因此，如何“幾何地”表示出等差數列中的項呢？如何將“數之和”轉化為“幾何對象的某種度量之和”？從而想到從幾何角度的解決方法：補形法。

具體的教學設計這里就不完整寫出了。需要說明的是，在上面的過程中，可以將相關的文化元素揭示出來，給學生提供延伸閱讀的材料，如與“垛積術”相關的數學史料。