“問題·賬戶·系統”學習法*

2021-04-21 07:58:50山東省實驗中學250109張蘊祿

中學數學研究(廣東) 2021年5期

山東省實驗中學(250109) 張蘊祿

“讓學生學會學習”是世界各國課程改革的永恒主題.“教會學生學習”已成為當今世界流行的口號.我國著名教育家陶行知先生早就指出:“我以為好的先生不是教書,不是教學生,乃是教學生學.”數學課程改革的一個顯著特點就是要求關注學生的發展,激發學生學習數學的興趣,促進學生數學學習行為和習慣的改善.然而目前學生數學學習中的低效表現呼喚高效數學學習方法.

1 數學學習中的低效表現

很多學生認為學習數學就是解題,解一道一道的具體題目.學生每天在書山題海中跋涉,做了大量的題目.說做題甚至都已經過時了,應該叫“刷題”(據說有的學校高中三年僅數學試卷摞起來竟達280cm 高).然而在很多情況下,學生的做題數量與取得的成績是不相匹配的.經常聽到家長說“孩子每天都熬夜到很晚,用了大量的時間做數學作業可是數學成績仍鮮有提高”.很多學生,老師講時也能明白,做過的題目過幾天就忘了,于是反復練、重復練就成了家常便飯.經常聽到老師們抱怨“這個題講了n遍了,還是這么多學生出錯”.種種跡象表明很多學生的數學學習是低效率的.

2 數學學習效率低的成因分析

美國數學家哈爾莫斯認為,問題是數學的心臟,數學的真正組成部分是問題和解.數學問題是數學學習的基本要素,學習數學就是“問題解決”, 而數學題是數學問題的一個載體,是數學問題的具體呈現.學習數學離不開解題,著名數學家華羅庚曾說過“學習數學不做題如入寶山而空手歸”.但是如果解題只是就題論題、淺嘗輒止,而看不到題目所蘊含的數學本質,面對稍微靈活一點的題目便會無所適從.究其原因是因為學生缺乏問題意識,僅靠多做題,只是就題論題,這種數學學習總是碎片化的,是缺乏邏輯性和系統性的,也一定是低效能的,因為沒有整體系統的知識是容易丟失的,沒有邏輯關聯的知識是容易偏離的.

例1已知橢圓的中心在坐標原點O,焦點在坐標軸上,直線y=x+1 與該橢圓相交于A、B兩點,且滿足OA⊥OB,求橢圓的方程.

例2已知直線l過點且與橢圓相交于C、D兩點,求證以CD為直徑的圓過定點E(1,0).

例3已知橢圓= 1 外一點M(m,0)(m ＞傾斜角為的直線l交橢圓于C、D兩點, 若點N(3,0)在以線段CD為直徑的圓E的外部,求m的取值范圍.

例4已知直線l過點且與橢圓相交于C、D兩點,試問: 在坐標平面上是否存在一個定點T,使得無論l如何轉動,以AB為直徑的圓恒過點T? 若存在,求出點T的坐標;若不存在,請說明理由.

以上4 個題目都是圍繞同一個問題編擬的, 即“垂直問題”.例1 設A(x1,y1),B(x2,y2) 根據OA⊥OB列出x1x2+y1y2= 0 而解答.例2 以CD為直徑的圓過定點E,實質上還是EC⊥ED.例3 點N在以線段CD為直徑的圓E的外部,等價于例4 與例2 的區別就是例2 中點E的坐標是已知的,而點T的坐標是未知的,理解到這一點,只要能求出點T的坐標(比如運用特殊值法)剩下的就應該與例2 相同了.盡管4 道題目圍繞同一個問題,且題目與題目之間僅僅是細微的變化,但就是這每一次的細微變化,都會阻礙一些學生的腳步.由于4 道題目學生不會同時遇到,如果學習僅僅就題論題、碎片化的,等遇到后面的題目時前面的題目就已經忘記了,老師的每一次講解都要另起爐灶、重新開始.即便是4 道題目全部做過,由于4 道題目分別在不同時段,且沒有很好的整合,也很難認識到這類題目的本質規律.也就是說學生學習效率低的原因是在很大程度上是沒有很好的發揮已做題目的作用.

3 “問題·賬戶·系統”學習法

“問題·賬戶·系統”學習法是指學生在數學學習過程中,從數學問題及其解法或者是定理、性質、結論等提煉出一般性的數學問題中,建立一個屬于該一般性數學問題的賬戶,在后續的學習中圍繞這一問題逐步進行積累、建構、進而形成一個完善的數學問題系統的數學學習方法.“問題·賬戶·系統”學習法有提煉問題、建立賬戶、積累構建、形成系統幾大基本步驟.

“問題·賬戶·系統”學習法遵循建構主義原理,通過給數學問題建立賬戶的形式,不斷積累與建構數學問題,逐步形成數學問題系統.完善的數學問題系統的形成意味著能從數學問題千變萬化的具體呈現中洞察其來龍去脈、把握其本質規律.“問題·賬戶·系統”學習法強調在原有知識體系的基礎上構建,重視舊知與新知的整合,最大限度的發揮已做題目的作用,真正做到“經歷+總結=提高”,進而提高解題效率.

例1-例4 僅僅是“垂直問題”的幾個變式而已,其實關于垂直問題的變式還有很多,如果每遇到一次變式,就把這一問題補充完善、梳理整合,積累到一定程度,認識到這類問題的本質規律也就是水到渠成的事了.

4 “問題·賬戶·系統”學習法的實施

4.1 提煉問題、建立賬戶

學習數學要有問題意識,要善于發現問題、提出問題、提煉問題,只有提煉出問題才有可能給所提煉的問題建立一個“賬戶”.也只有給問題建立起一個賬戶,才能圍繞這一問題逐步進行構建,逐步存儲一些有價值的東西.這就和銀行存款一樣,只有在銀行建立一個賬戶,才能不斷向這一賬戶存款.如果沒有問題意識、賬戶意識,那么學習數學就只剩下解題了.

前文所述,如果解答例1 時就給垂直問題建立一個賬戶,解答例2-例4 時及時積累關于垂直問題的一些變式,那么就會對這一問題的認識越來越深刻,積累到一定程度,就會出現任其垂直問題千變萬化總能透過現象看到本質的東西.再看下面的例子.

例5若0＜a ＜1,且函數f(x) =|logax|,則下列各式中成立的是

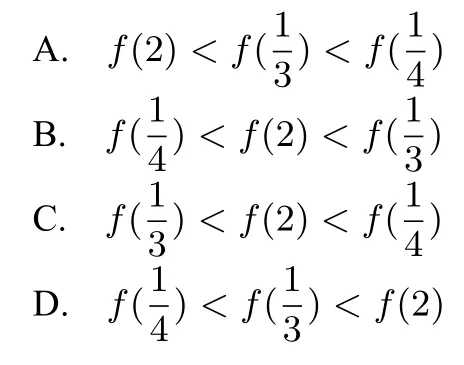
這是課本上的一道傳統題目,運用數形結合(如圖1),其本質就是f(a)=f(b),則ab=1.答案選A.

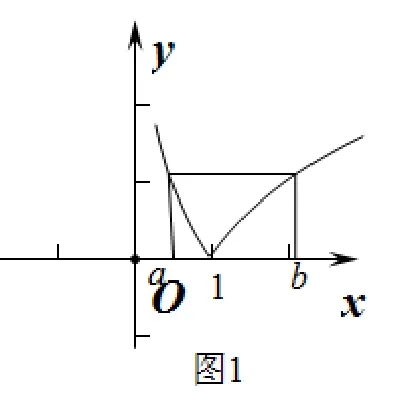
如果解答此題僅是就題論題,求解之后沒有做過多思考,也沒有進一步提煉出這道題目所涉及到的問題,那么解此題的效率就很低了.

例6(2010 高考全國新課標Ⅰ卷理科第10 題)已知函數f(x) =|lgx|,若0＜a ＜b,且f(a) =f(b),則a+2b的取值范圍是

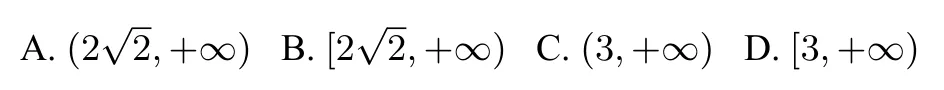
例7設方程3x=|lg(?x)|的兩個根為x1,x2,則

A.x1x2＜0 B.x1x2=0 C.x1x2＞1 D.0＜x1x2＜1

例8已知函數f(x) =若0＜a ＜b ＜c,滿足f(a) =f(b) =f(c),則的取值范圍是_____.

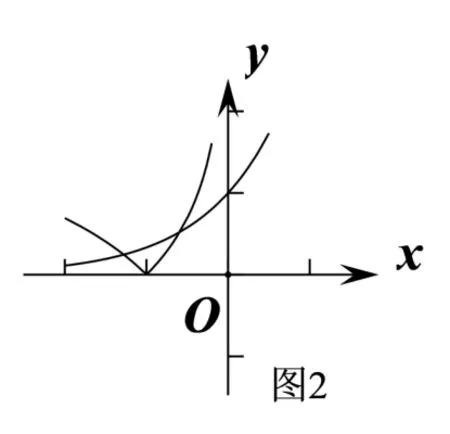
分析對于例6,不難得到a+2b=a+然后再利用“對勾”函數的性質, 可得出答案選C.對于例7, 如圖2, 此題就是在原來例5 的基礎上進行了一些變化,但是無論如何變化,只需抓住y=|ln(?x)|的性質,就能體會變中的不變,答案選D.對于例8,只要理解好f(x)=|logax|(a ＞0,a/=1)的性質,就能得到ab= 1,然后只需求出的范圍即可,答案為(1,2).

如果學生第一次遇到例5 時, 就提煉出函數f(x) =|logax|(a ＞0,a/=1)的性質,并及時給這一問題建立一個賬戶,在以后的學習中再碰到諸如例6-例8 中的問題,及時進行補充、完善,把前后問題整合在一起,那么這種學習就是圍繞問題在學習.如果圍繞這一問題不斷積累,就會發生有量變到質變的飛躍,這就是我們經常所說的厚積薄發.

4.2 積累建構、形成系統

提煉問題、建立賬戶后,根據學習的進展,要逐步補充完善,每一個問題要有足夠的題目或變式作為支撐,也就是說這個問題要有一個基本骨架,有了這樣一個基本骨架,才叫有了“形”,進而形成一個有血有肉的有機整體,形成一個數學問題系統.盡管說問題和具體題目不是一回事,但是問題還需要具體題目來呈現.

例如前面圍繞函數f(x) =|logax|(a ＞0,a /= 1)的性質所建立的賬戶,盡管存儲了諸如例5-例8 等題目后已經不再是干巴巴的性質而是有血有肉的一個小的單元,或著具有了一個“雛形”,但僅有這幾個題目還不足以支撐起這一問題的整個系統.

例9已知函數f(x)=若0＜x1＜x2＜x3, 滿足f(x1) =f(x2) =f(x3), 則的取值范圍是____.

例10已知函數f(x)=若?1＜a ＜b ＜c ＜d,滿足f(a) =f(b) =f(c) =f(d),則a+b+c+d的取值范圍是____.

例11(2018年全國高中數學聯賽(B) 一試第10 題) 已知定義在(0,+∞) 上的函數f(x) 為f(x) =設a,b,c是三個不相等的實數,滿足f(a)=f(b)=f(c),求abc的取值范圍.

分析例9 就是把例8 中的函數進行了平移,由此變成了(x1+1)(x2+1)=1.理解了此種變化問題就不難解決了,答案仍為(1,2).例10 是把例9 中的分式函數變成了二次函數,(a+1)(b+1) = 1,c+d= 4,就可以求出a+b+c+d的取值范圍是(4,+∞).例11 就是把函數y= log3x平移和翻折變換,此時f(a) =f(b)已不再是a,b互為倒數,而是ab=32=9,但本質上還是一樣的,其具體解法如下:

解不妨設a ＜b ＜c, 則a ∈(0,3),b ∈(3,9),c ∈(9,+∞), 因為f(a) =f(b), 1?log3a= log3b ?1, 所以ab=32=9,于是abc=9c.又因為0＜f(c)=4?所以c ∈(9,16),故abc ∈(81,144).

例5-例11 盡管都屬于“函數f(x) =|logax|(a ＞0,a /=1)的性質”問題.題目考查點各有側重,難度也各有不同,有課本題目、也有高考試題,還包括競賽題目,但歸根結底都與函數f(x) =|logax|(a ＞0,a /= 1)的性質有關.如果說例5-例8 是這一問題的雛形,積累到例9-例11,就構建起了一個比較完善的系統了.如果構建起了這樣一個系統,那么學生對這一問題的認識就不會再是就題論題了,就能從千變萬化中洞察和把握其中的本質規律.我們經常說題目萬變不離其宗,此時學生就能夠抓住這個宗.這類問題的宗就是無論題目怎么變化,都要圍繞函數f(x) =|logax|(a ＞0,a /= 1)在“區間(0,1)上單調遞減,在區間(1,+∞)上單調遞增”以及的本質.當然題目變化之后,這一本質也會出現一些新的呈現方式(例如例9 中變成(a+1)(b+1)=1,例11 中f(a) =f(b)變為ab= 9),但是無論如何變化,都是圍繞這一性質的變化.如果學生能抓住這一點,千變萬化的一道一道的具體題目呈現在面前時,就能夠不畏浮云遮望眼了,甚至學生都可以自己編題了.

當然不可否認,某些數學天分極高的學生在例5 的基礎上就能直接上升到例11 的問題,甚至是有能力直接解答例11,但是據筆者多年的教學實踐,如果僅僅是給問題建立了賬戶,而圍繞問題的積累還非常單薄,還不具備足以構建起支撐起這一問題基本變化系統,還是不能游刃有余的解決此類問題的.任何一個問題系統都有構成這一問題系統的基本要素,也就是說這個系統應包含這類問題數學本質、以及數學本質的具體呈現形式,處理這一類問題的基本規律、技巧,以及學生在解決這類問題中容易出現的錯誤等等都屬于這個問題系統的構成要素.當然構建起的系統也不是內容越多越好,整個建構過程應該是一個去粗取精、去偽存真的過程,也是一個因人而異的過程.“問題·賬戶·系統”學習法是要給所有的(既包括天分極高、也包括看似天分不高的)學生提供一種知識梳理與盤點的學習方法,只是面對同一問題,其梳理與積累的方法和耗費的精力因人而異罷了.

也許有人說,為什么老師講解例5 時不把這些變換給學生講清楚呢? 事實上,由于受時間、課時,以及學生接受能力的限制,圍繞這一問題的諸多題目是不可能一下子給學生呈現的,因為這也違背了分層遞進、螺旋上升的認知規律,以及夠一夠摘桃子的“最近發展區”理論.整個積累完善的過程應該是先由教師引導,最終要變成一個學生的自發行為.目的是讓學生掌握一種梳理知識、總結反思的學習方法.另一方面如果僅僅看到問題的“終點”或是較高目標點,而忽視數學問題系統的構建過程結果也會適得其反.

例12(2012年高考山東卷理科第21 題) 已知函數(k為常數,e=2.71828···是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與x軸平行.

(1)求k的值;

(2)求f(x)的單調區間;

(3)設g(x) = (x2+x)f′(x),其中f′(x)為f(x)的導函數.證明: 對任意x ＞0,g(x)＜1+e?2.

分析例12 是2012年山東高考理科的壓軸題,當時得分率很低,特別是(3)更是很少有考生問津,更不用說得分了.(3)實際上就是要證明當x ＞0 時,1 + e?2.而要完成此不等式的證明很多考生就會無所適從, 但是只要熟悉不等式“ex ＞ x+ 1(x ＞0) ”就可把不等式變形為(1?x ?xlnx)＜1 + e?2, 而只需證明1?x ?xlnx≤ 1 + e?2,或者說只需求出h(x) = 1?x ?xlnx(x ＞0) 的最大值就可以了, 這就把壓軸題變成一個十分簡單的問題了.其實此題就是表達式的“變形與轉化”問題中的一種情況,如果不把這種情況納入到整個“變形與轉化”系統中,按照由淺入深的原則進行積累與建構,即便是老師講過了,再遇到類似問題學生還會無所適從.這就是老師們經常抱怨的“這種題該會的不講也會,不會的講了也不會”.一個主要原因是作為老師沒有關于“變形與轉化”的問題系統,更沒有引導學生逐步積累與建構的意識,只是把目標定位在了問題的較高目標點.

5 “問題·賬戶·系統”學習法的成效

案例1課堂教學中筆者曾結合某些高考或模擬題講過拋物線一個常用性質.有個名叫關樂萌的同學運用“問題·賬戶·系統”學習法,對此類問題不斷積累、不斷完善,完成了論文《一個久考不衰的拋物線的性質》.

案例2一次老師課堂上講到巧妙利用對稱性使圓錐曲線題目不再困難.一個名叫孔湛琦的同學對圓錐曲線中對稱性的應用進行了積累和梳理,完成了《用對稱性求解圓錐曲線高考題》.

案例3課堂教學中筆者講過向量的拆分技巧.一個名叫朱靜怡的同學在筆者所講例題的基礎上不斷積累、拓展最后完成了論文《關于高中數學學習中萬變向量的拆分》.

以上幾個案例只是眾多案例的幾個典型代表,筆者的很多學生作品或發表于各類報刊、雜志,或在各級各類比賽中獲獎.新課程已經將數學探究、數學論文寫作提高到非常重要的地位,有很多教師還在為評職晉級沒有論文發表而焦急的時候,我們的學生竟能在一些重要期刊上發表自己的論文,這不能不說這些學生掌握了一種高效的學習方法.每當看到自己學生的作品發表或獲獎,心里都有一種溢于言表的自豪和幸福感.筆者感到高興的絕不僅僅是學生取得的成績,更重要的是看到學生已經掌握了一種行之有效的高效學習方法,真正實現了授人以魚不如授人以漁.