圓助攻,巧解三角形最值問題

廣東省佛山市第四中學(528000) 黃 儀

解三角形中的最值問題,一般是利用正余弦定理,結合基本不等式,或三角函數的有界性,二次函數的最值等方法求解,但通常會推導過程繁冗,計算量大,容易出錯,尤其是選擇填空題,做題耗時過多,得不償失.三角形中角度和邊長的變化,其實就是平面幾何中點和線的變化,能否跳出知識的局限,利用平面幾何輔助解題? 平面幾何中的圓,由于其半徑和圓心角,圓周角的特性,往往成為一個很好的解題助力工具.

一、角的轉化

三角形中,當點動而角不變時,如果定角所對的邊也是定值,求最值問題時,可將角轉化為同圓中同弧所對的圓周角或圓心角, 利用同弧所對的圓周角或圓心角不變的性質,化動為靜.

例1(2014 高考新課標Ⅰ卷理科) 已知a,b,c分別為ΔABC的三個內角A,B,C的對邊,a= 2 且(2 +b)(sⅰnA ?sⅰnB) = (c ?b)sⅰnC, 則ΔABC的面積的最大值為____.

解由正弦定理, (2 +b)(sⅰnA?sⅰnB)=(c?b)sⅰnC即(2+b)(a?b)=c(c?b),將a=2代入整理得b2+c2?a2=bc,所以cosA=邊a為定長2,角A為定值, 構造ΔABC外接圓O, 則點A可看作圓O中所對的圓周角∠BAC的頂點,由垂徑定理易知當AO⊥BC時,ΔABC的面積最大,為

圖1

評析這是一道求面積最值的經典題目,方法多樣.構造圓,利用幾何輔助解題是最靈活,計算量最少的解法.通過角度不變,點A可看作在圓周上運動,角A兩邊長的變化轉化為三角形高的變化,求面積的最值即求高的最值.

例2ΔABC中, ∠ABC= 90°,AC= 2BC=P是ΔABC內一動點,∠BPC= 120°,則AP的最小值為____.

解以BC為x軸,BA為y軸建立平面直角坐標系, 構造圓O, 使BC為圓O的弦, ∠BPC為優弧BC所對的圓周角恒為120°, 則點P的運動軌跡為弧BC.線段AP的最小值就轉化為點A到弧BC的距離的最小值.由BC=圓心角∠BOC= 120°易知O點坐標為, 圓O半徑為2, 則AP的最小值=|OA|?|OP|=

圖2

評析此處巧妙地用了平面幾何與解析幾何中圓的性質.首先由動點P形成的角為定值,將點動轉化為角動,根據角度不變構造出同弧所對的圓周角,再將AP的值轉化為點到圓的位置關系求解,利用坐標系大大簡化了計算量.

二、邊的轉化

三角形中,點動,角變,而邊不變,結合圓中的定長為半徑或直徑,可將三角形中的一條動邊構造為圓的半徑或直徑,將點動轉化為圓中半徑位置的轉動,進而引起其他頂點或角度的變化,再結合圓的性質,求出相應的取值范圍.

例3在ΔABC中,AB= 1,BC= 2,求角C的取值范圍.

解以B為圓心,AB= 1 為半徑構造半圓, 當頂點A從點M沿著半圓弧運動到點N的過程中, 角C從零開始, 先逐漸增大,當CA與半圓B相切時,角C最大,為30°,然后又逐漸減小至零,得出角C的取值范圍是(0,30°].

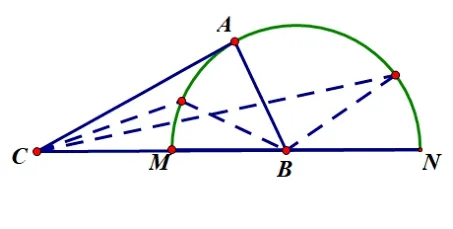
圖3

評析本題中角C的對邊為定值,以定長為半徑構造圓,當角C變化時,點A在半圓周上運動,角C的值隨著角A的變化而變化,由角A的取值范圍得出角C的取值范圍.這一招可謂“動中求變化,變中有方法”!

三、三角形的轉化

平面四邊形中,某動點在變化,帶動其它的點也在對應變化(這兩個稱之為對應點),相當于整個圖形在變化,其中蘊含著變化的三角形與不變的對應關系,將其中變化的三角形構造圓,對應點利用其對應關系也構造出相應的圓,兩圓相結合輔助解題,事半功倍.

例4在平面四邊形ABCD中,AD= 2,CD= 4,ΔABC為正三角形,則ΔBCD面積的最大值為____.

圖4

解以點C為原點,CD為x軸建立平面直角坐標系, 則D(4,0), 由AD= 2,CD= 4 可知點A在圓D: (x ?4)2+y2= 4 上, 因為是點A繞原點C旋轉60°得到點B,所以點A的軌跡圓D繞原點C逆時針旋轉60°所得點B的軌跡圓E,可求得所以點B(x,y)在圓E: (x ?2)2+= 4 上,易知|y|≤所以有ymax=所以ΔBCD面積的最大值為

評析本題中點A,C在變化,帶動點B也在動,其不變關系是等邊ΔABC.構造出動點A作圓周運動的圓D,再根據等邊三角形中的定角∠ACB及等邊,得出動點B的運動軌跡圓E,相當于把ΔACD旋轉到ΔBCE,動點B的的運動過程,就是ΔBCD高的變化過程,從而確定面積的變化.本題是“點(A)動——點(B)動——線(高)動”的變化過程,構思巧妙,技巧性強.

例5如圖5 在凸四邊形ABCD中,AB=1,BC=√AC⊥CD,AC=CD,當∠ABC變化時,對角線BD的最大值為____.

解以B為圓心,AB半徑構造圓B,以C為圓心,將圓B旋轉90°得到圓E,則∠BCE= 90°,BC=CE=BE=當點A在圓B上運動時,點D在以E為圓心,1為半徑的半圓上運動,由圖得BD的最大值即BE的長加圓E的半徑,即√

圖5

評析本題與例4 異曲同工,也是構造雙圓輔助解題.將ΔABC旋轉變換到ΔDEC,即圓B變換到圓E,即利用點A的運動軌跡求出點D的運動軌跡,此時,即可眼前一亮,豁然開朗,進而結合圓的性質解出此題.

三角形的轉化,其實就是邊和角的轉化,歸根到底還是根據點的運動、點和線的變化,把點、線的運動與圓相結合,構造圓解題.借助圓這個工具,解題跳出知識的局限,回歸平面幾何與解析幾何的本質時,則可以從幾何要素點、線、角、三角形等角度,將問題轉化為觀察變化規律的幾何問題,避免大量的三角運算,縮短解題時間,化繁為簡.

在教學中,要求學生有較強的抽象思維能力以及平面幾何,空間幾何的想象能力,平時多觀察,多思,多練,多畫(圖),跳出思維的框架,發揮想象的空間;還要善于將知識點融會貫通,綜合運用,將三角函數與平面幾何、解析幾何綜合運用,靈活轉換,學生要有扎實的數學基礎和培養良好的數學素養;最后要有模型意識,善于建立數學模型.與圓相結合的解三角形問題具有較高的特定性和技巧性,需要在實際解題過程中多體會模型的特征,提高解三角形問題的幾何意識.