一題五探

山西省太原市第三實驗中學(030031) 董立偉

普通高中課程標準實驗教科書《數學4·必修·A 版》(人民教育出版社,2007年2月第2 版)第147 頁復習參考題B組第7 題如下:

題目如圖1,正方形ABCD的邊長為1,P,Q分別為邊AB,DA上的點.當ΔAPQ的周長為2 時,求∠PCQ的大小.

與教科書配套的《教師教學用書》第131 頁給出了本題的如下基于三角恒等變換視角的解答:

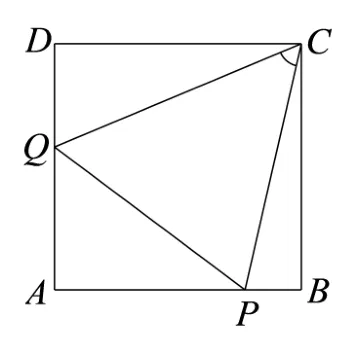
圖1

設AP=x,AQ=y, ∠BCP=α, ∠DCQ=β, 則tanα=1?x,tanβ=1?y.于是

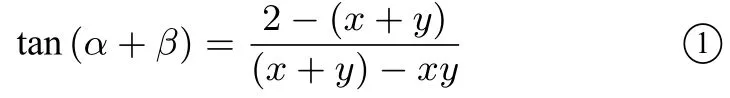
又ΔAPQ的周長為2,即x+y+變形可得

于是tan(α+β) =又0＜α+β ＜所以α+β=

本文沿用上述解答中各幾何量的表示法,在此基礎上對本題做深入探究.

探究一本題還有其他的解題視角嗎?

解法一(平面向量的視角)建立如圖 2 所示平面直角坐標系.則P(x,0),Q(0,y),C(1,1).所 以,(x ?1,?1),= (?1,y ?1).cos ∠PCQ=

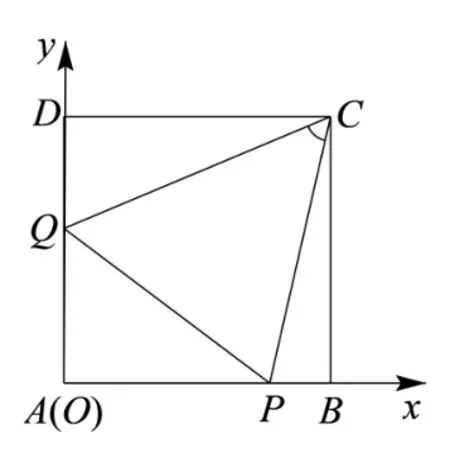
圖2

展開即

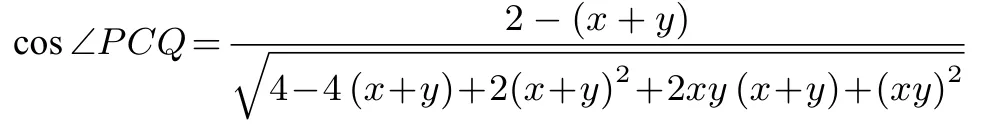
將②代入上式并化簡得到

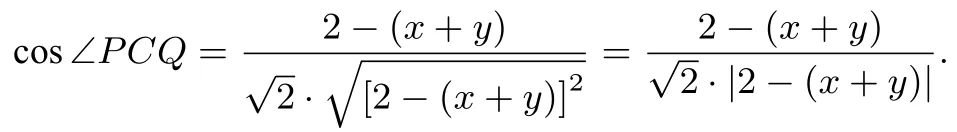
因為0＜ x,y ＜1, 所以, cos ∠PCQ=又因為0＜∠PCQ ＜所以,∠PCQ=

解法二(解三角形的視角)AP=x,AQ=y, 所以PB= 1?x,QD= 1?y,PC== 2?(x+y).在ΔCPQ中,由余弦定理有

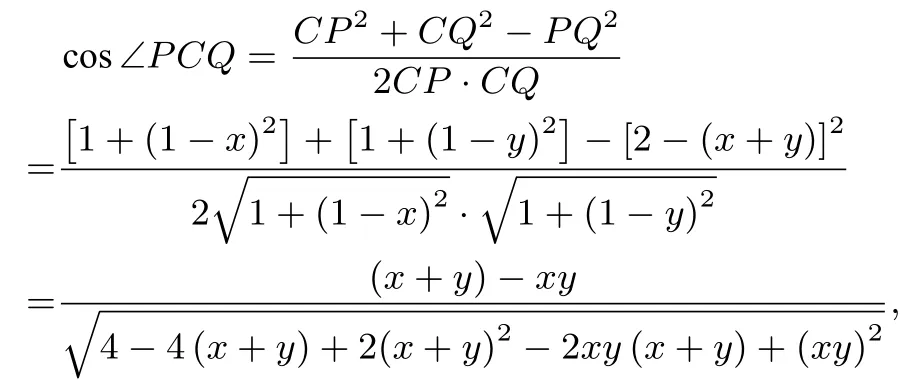
將②代入上式并化簡得

因為0＜ x,y ＜1, 所以, cos ∠PCQ=又因為0＜∠PCQ ＜所以,∠PCQ=

解法三(平面幾何的視角)如圖3, 延長AB至點S, 使BS=DQ= 1?y,從而PS=PQ.連接CS,則CS=CQ.所以, ΔCPQ∽= ΔCPS,ΔBCS∽= ΔDCQ.故

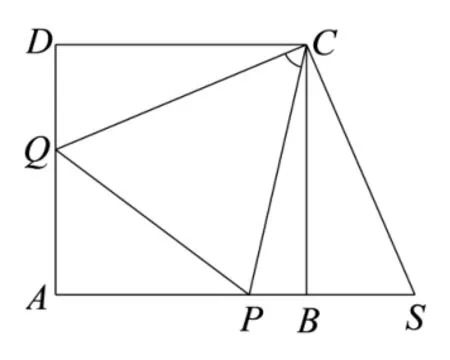
圖3

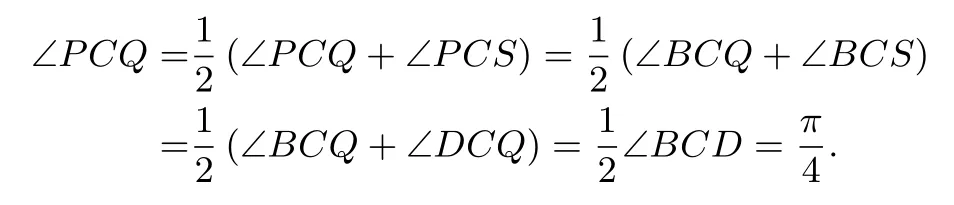
注1解法三說明,當ΔAPQ的周長為2 時,若過點C作線段PQ的垂線CR(垂足為R),則有以下三個結論成立:

結論1|CR|=1.

結論2 ΔPCQ是由ΔBCP與ΔDCQ分別沿CP與CQ翻折至邊CB、CD重合而得.

結論3 點R分線段PQ所成比為

探究二ΔAPQ的周長為其他定值時,∠PCQ是一個定值嗎?

設ΔAPQ的周長為n(0＜n ＜2+則x+y+=n.變形可得

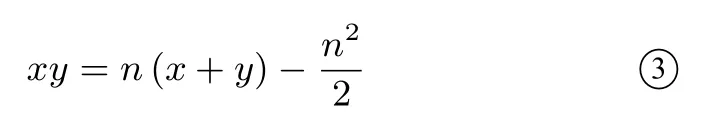
將③代入①, 得tan(α+β) =如果∠PCQ是定值,則解得n=2.故當且僅當ΔAPQ的周長為2 時,∠PCQ是一個定值.

探究三如何找出所有的周長為2 的ΔAPQ?

我們首先解決如下問題:當ΔAPQ的周長為2 時, 線段PQ上使得的點R的軌跡是什么圖形? 建立如圖4 所示平面直角坐標系,設R(x,y).由注1,R點是由ΔBCP與ΔDCQ分別沿CP與CQ翻折至CB與CD重合而得,且|CR|=1.不妨設Q(0,y0).則有

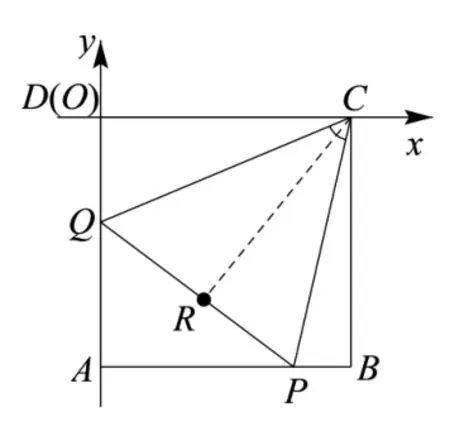
圖4

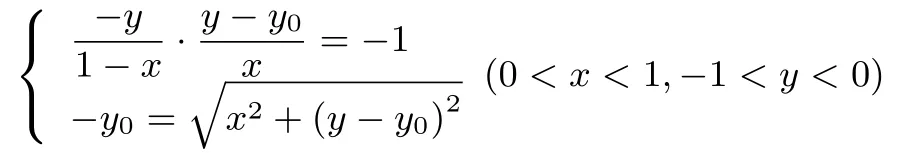
聯立消去y0得點R的軌跡方程為(x ?1)2+y2= 1(0＜x ＜1,?1＜y ＜0).故點R的軌跡是以點C為圓心,1 為半徑的圓落在正方形內的部分(不含端點B和D).

下面,我們解決如何找出所有的周長為2 的ΔAPQ的問題.以點C為圓心,1 為半徑作圓,記落在正方形ABCD內的圓弧為在圓弧(不含端點B、D)上任取一點R, 過點R作圓C的切線(或者過點R作與RC垂直的直線), 分別交線段AB、AD于P、Q兩點, 則ΔAPQ即為所求.

探究四ΔAPQ的周長為2 時,ΔCPQ的面積的取值范圍是什么?

由②,y=(0＜ x ＜1).PQ= 2?x ?CR= 1.設ΔCPQ的面積為f(x).則f(x) =當x ∈0,2?時,f′(x)＜0; 當x ∈時,f′(x)＞0.所以,f(x) 在單調遞減, 在單調遞增.從而,當x=y= 2?時,ΔCPQ的面積f(x)取得最小值又因為f(x)＜f(0) =所以,ΔCPQ的面積的取值范圍是

注2如果探究四的問題改為: ΔAPQ的周長為2時, ΔCPQ的面積的最小值是多少? 則可以利用基本不等式求解.過程如下: 將xy≤代入②得,2(x+y)?2 ≤,化簡得(x+y)2?8(x+y)+8 ≥0.由0＜ x,y ＜1 得,x+y≤ 4?所以,PQ=2?(x+y) ≥2?(故SΔCPQ=等號當且僅當x=y=2?成立.

探究五ΔAPQ的周長為2 時,ΔCPQ的周長的取值范圍是什么?

我們先證明如下引理成立.

引理若m(x)是定義在區間D上的取值恒為正數的可導函數,則m2(x)與m(x)具有相同的單調性.

證明記M(x) =m2(x),x ∈D.則M′(x) =2m(x)·m′(x).因為m(x)＞0,所以M′(x)與m′(x)同正負.故m2(x)與m(x)具有相同的單調性.

下面解決ΔAPQ的周長為2 時,ΔCPQ的周長的取值范圍是什么的問題.

設ΔCPQ的周長為g(x),則

將y=代入,得g(x)=(0＜x ＜1).記

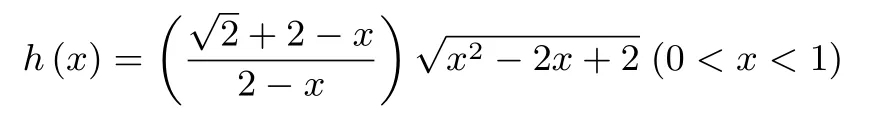
H(x)=[h(x)]2=(x2?2x+2)(0＜x ＜1),i(x)=2?x ?(0＜x ＜1).因為h(x)＞0,由引理,H(x)與h(x)具有相同的單調性.

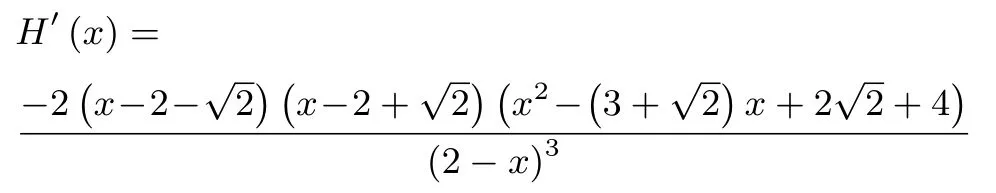
當x ∈時,H′(x)＜0;當x ∈時,H′(x)＞0.所以,H(x)與h(x)均在(0,2?單調遞減,在單調遞增.從而,當x= 2?時,h(x)取得最小值h(x)＜h(0) =h(1) =+1.又由探究四可知,i(x) = 2f(x).所以, 當x ∈(0,2?時,i′(x)＜0; 當x ∈時,i′(x)＞0.故,i(x) 在單調遞減, 在單調遞增.從而, 當x= 2?時,i(x) 取得最小值i(x)＜i(0) =i(1) = 1.所以, ΔCPQ的周長的取值范圍是

一點感悟這一試題本是高中數學內容“三角恒等變換”下的一道復習參考題.在探究中卻發現,它與平面向量、解三角形、平面幾何、解析幾何、函數與導數等內容都有聯系.內涵之豐富實屬預料之外.這給我們的高考復習提供了一種借鑒,即應當對教材習題做深入研究,探索其隱藏的問題、與其他內容之間的聯系及蘊含的解題思想方法,讓復習更為高效.