有心圓錐曲線的一個性質(zhì)

陜西省西安市臨潼區(qū)教學(xué)研究室(710600) 王江河

題目1(2017年廣東揭陽一模文數(shù)第20 題.) 已知橢圓= 1(a ＞的離心率為,點(diǎn)M、N是橢圓C的點(diǎn),且直線OM與直線ON斜率之積為

(1)求橢圓C的方程;

(2)設(shè)動點(diǎn)P(x0,y0)滿足是否存在常數(shù)λ,使得點(diǎn)P是橢圓=λ上的點(diǎn)?

反思解題過程略,此題第二問結(jié)論是存在常數(shù)的,那么這個常數(shù)與題中那個量關(guān)系密切呢? 第二問能做一般化考慮嗎? 經(jīng)過筆者探求發(fā)現(xiàn)有心圓錐曲線一個完美的結(jié)論.

性質(zhì)1已知點(diǎn)M、N在有心圓錐曲線C:1(m,n至少一個為正數(shù),m·n /= 0) 上, 若點(diǎn)P滿足當(dāng)直線OM與直線ON斜率之積為定值時,則點(diǎn)P落在圓錐曲線上.

證明設(shè)M(x1,y1),N(x2,y2),由設(shè)點(diǎn)P(x0,y0), 得x0=λx1+μx2,y0=λy1+μy2, 點(diǎn)M、N在橢圓C:= 1 上, 所以=mn.設(shè)

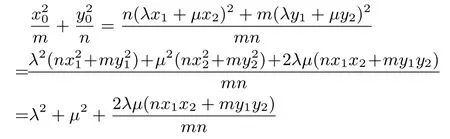
當(dāng)且僅當(dāng)nx1x2+my1y2=0 時,有

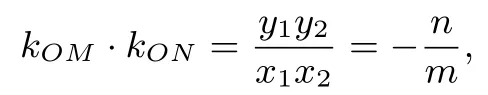
性質(zhì)2已知點(diǎn)M、N在有心圓錐曲線C:1(m,n至少一個為正數(shù),m·n /= 0) 上, 若點(diǎn)P滿足且點(diǎn)P在圓錐曲線=λ2+μ2上,則直線OM與直線ON斜率之積為定值

證明設(shè)M(x1,y1),N(x2,y2), 點(diǎn)M、N在橢圓C:=1 上,所以設(shè)點(diǎn)P(x0,y0),由得

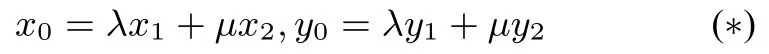
得到nx1x2+my1y2= 0.即有從而直線OM,ON斜率之積為定值

題目2已知點(diǎn)M、N是橢圓C:=1 上的點(diǎn),設(shè)動點(diǎn)P(x0,y0)滿足是否存在常數(shù)λ,使得點(diǎn)P在橢圓=λ上.

解由性質(zhì)1 得存在常數(shù)λ= 5, 使得點(diǎn)P, 在橢圓=5 上,此時M,N滿足kOM ·kON=