基于混合Copula函數的風電場可用慣量評估方法

韓 帥，張 峰，丁 磊，應 有

（1. 山東大學 電網智能化調度與控制教育部重點實驗室，山東 濟南250061；2. 浙江運達風電股份有限公司，浙江 杭州310012）

0 引言

隨著風電在電網中的滲透率不斷提高，大量火電機組被風電所替代，整個電力系統的可用慣量持續減少，頻率響應能力不斷降低。日益減少的火電機組逐漸難以獨立承擔不斷增加的調頻壓力，電網在一定程度上要求風電機組具備參與系統頻率調整的能力［1］。這種能力包含慣量響應［2-3］、一次調頻［4］以及二次調頻等多種時間尺度的頻率響應方式。

目前，國內外學者對于風電機組參與慣量響應的研究多集中于優化風機調頻控制策略方面。文獻［5］提出一種風機虛擬慣量控制方案，通過虛擬慣量控制，風電機組可以吸收或釋放轉動機構上的動能來響應電網的頻率波動。然而，風機轉速恢復需吸收能量，造成電網出現頻率二次跌落。文獻［6］引入風機轉子動能評估因子，根據該參數協調各臺風機參與頻率響應的方式，從而達到抑制頻率二次跌落的目的。文獻［7］提出通過超速備用控制使風機越過最大功率點跟蹤MPPT（Maximum Power Point Tracking）運行，風機轉子轉速預留了可觀的調頻裕度。文獻［8］在微電網運行環境下提出頻率和電壓的綜合控制策略，通過虛擬同步技術實現頻率的無差控制。

相較而言，針對風電機組或風電場參與電力系統調頻服務能力評估的研究相對較少。文獻［9］提出一種基于虛擬慣量控制原理的風機慣量響應能力評估方法，通過對大氣湍流的高斯概率分布模型進行分塊處理來評估出特定平均風速下的風電場聯合慣量響應能力。在此基礎上，文獻［10］綜合評估慣量響應過程中的虛擬慣量控制以及下垂控制的聯合調頻效果，結果顯示2 種控制方式的協調運行可提高風電場有功功率的輸出能力，提升風電場調頻性能。文獻［11］通過評估風力發電機組可用慣性動能KE（Kinetic Energy）來調整風機控制系統中虛擬慣量控制回路和下垂控制回路的增益。上述研究均提出確定慣量控制策略下的風電場可用慣量評估方法，但均忽略了尾流效應、風剪切效應等環境因素影響，未考慮風電場內各風機風速的時空分布特性，以及慣量響應過程中大氣湍流作用下的風速波動特性，且沒有計及實時運行中風機處于故障停機狀態對風機可用慣量的影響。綜上，現有評估方法忽略了風機的實時運行狀況，得到的風機可用慣量評估值與實際可用慣量間會存在誤差。若評估誤差過大，則風電場風機在參與慣性響應時無法按照控制策略預期來提供足夠的慣量，影響風機調頻效果。因而，有必要構建考慮風電場內各風機風速狀況和運行工況下的可用慣量評估方法，減小算法評估結果與實際值的誤差，提供高可信度的風電場可用慣量評估結果。

綜上，本文采用風電場測風塔測得的精度較高的風速信息，通過空氣傳播原理和混合Copula 函數構建風電場瞬時風速的概率分布模型。在此基礎上，分析虛擬慣量控制在電網頻率響應中的慣量釋放情況，進一步從能量和功率2 個方面給出風電機組實時可用慣量的概率化評估方法。

1 基于混合Copula函數的風電場風速建模

風電場風速分布是影響風機運行狀況的重要因素。通過對尾流效應、風剪切效應和時延效應進行分析可獲得風能在風電場的空間分布和時間變化特性，再利用Copula函數在相關性分析中的優勢，構建大氣湍流影響下的瞬時風速條件概率分布模型。

1.1 平均風速建模

（1）尾流效應。

尾流效應描述的是自然風從上游風機吹向下游風機時出現的風速遞減現象，目前，使用最為廣泛的是Jensen 尾流模型［12］，其計算基礎為風機尾流擴張理論，原理如附錄A 圖A1 所示。結合文獻［12］，綜合考慮風電場內各臺上游風機對下游風機j 的尾流效應，得到風機j的平均風速表達式如式（1）所示。

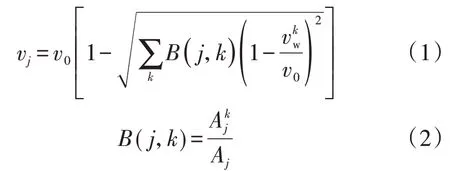
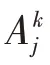
（2）風剪切效應。

風剪切效應是風速隨垂直高度增加而增加的現象，對于山地等復雜地形中的風電機組，風剪切效應影響較為顯著。考慮風剪切效應，風速可表示為：

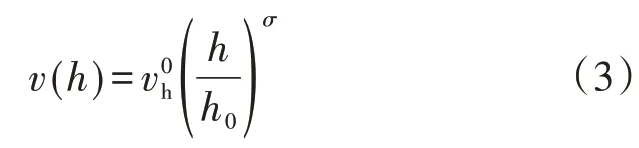
風電場實時風況從上游風機傳遞到下游風機時存在明顯的時間延遲，并且在考慮尾流作用的情況下，風速的時延現象尤為明顯。假定風速從風電場場端到風機j 的延遲時間為τ，延遲后上游風機風速為v0(t?τ)，結合式（1），得到時延效應下風機j 處的風速vj(t)為：

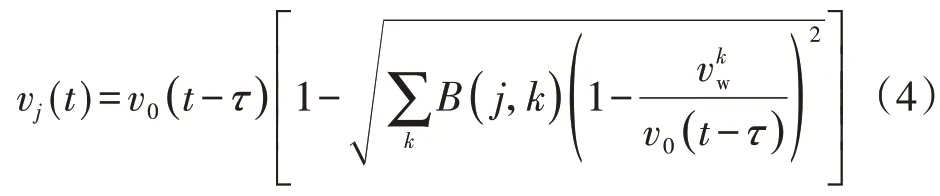
1.2 Copula函數

本節利用Copula函數進一步精細化描述考慮大氣湍流影響的瞬時風速概率分布狀況。Copula理論是Sklar 在1959 年提出的一類描述多變量相依關系的方法［13］，Sklar 定理指出，存在一個Copula 概率分布函數C(?)，對任意的x ∈Rn（n為樣本數），有：

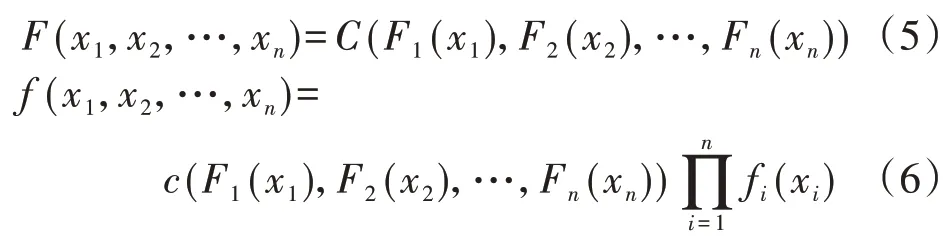
其中，c(?)為Copula 概率密度函數；x1、x2、…、xn為x內隨機變量；Fi(xi)和fi(xi)分別為隨機變量xi的邊緣分布函數和邊緣密度函數。令ui=Fi(xi)，則c(?)可表示為：

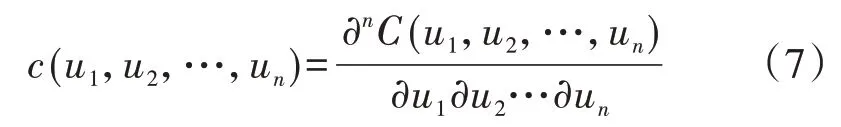
混合Copula函數的相關結構比單個Copula函數更加靈活，可以反映不同隨機變量間的相關模式。文獻［14］對混合Copula 函數理論進行了總結歸納，據此，得到式（8）所示的三元混合Copula函數。

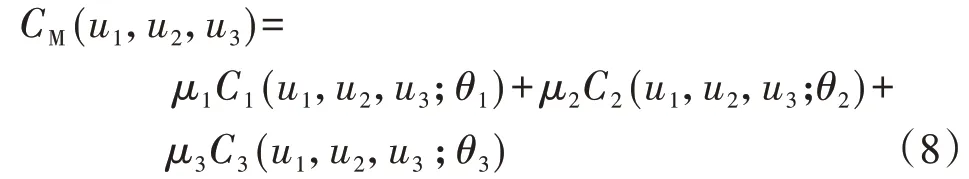
其中，μ1、μ2、μ3為權重系數，滿足μ1+μ2+μ3=1；C1(?)、C2(?)、C3(?)為3類不同的Copula函數；θ1、θ2、θ3為各Copula函數的相關系數。

1.3 瞬時風速概率分布模型

考慮到實時運行時風電場受大氣湍流作用，場內風速具有較大的波動性，在對風電場風速進行精確刻畫時，認為風機輪轂高度處的瞬時風速在慣性響應中是變化的。因而，本文提出利用混合Copula函數建立考慮瞬時風速、湍流強度以及平均風速的三元聯合分布函數，流程如圖1所示。

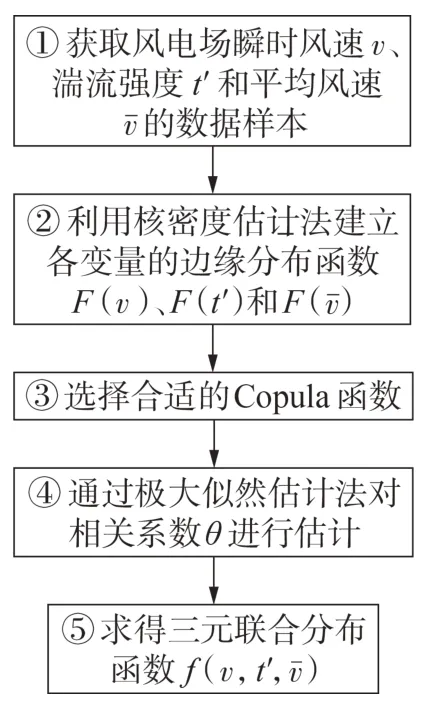
圖1 風電場風速聯合分布函數構建流程圖Fig.1 Construction flowchart of wind speed joint distribution function of wind farm

核密度估計KDE（Kernel Density Estimation）法是一種應用較廣泛的非參數估計方法。在圖1的步驟②中，通過KDE可構建的概率密度函數為［15］：

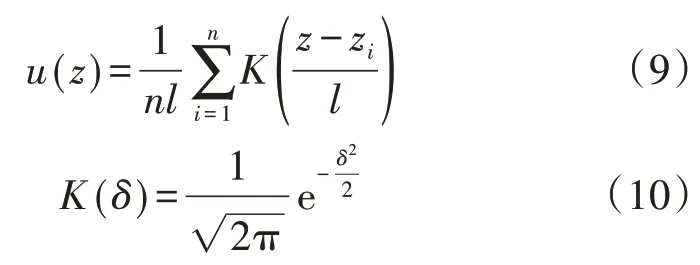
其中，z 為核密度函數自變量；zi為樣本點i 的數據；l為窗寬；K(δ)為高斯核函數，δ為核函數自變量。

通過對風電場的風速和氣象數據進行KDE 處理，可得到瞬時風速v、湍流強度t'和平均風速的邊緣密度函數f(v)、f(t')和f，再通過對邊緣密度函數積分獲得所需邊緣分布函數F(v)、F(t')和F。

Clayton-Copula、Gumbel-Copula 和Frank-Copula函數分別適合描述下尾部、上尾部和對稱數據的相依關系，分別記為CC(?)、CG(?)和CF(?)。圖1 的步驟③和④綜合3 種函數的優點，建立風速的三元混合Copula函數。其中，uv、ut'和分別為瞬時風速v、湍流強度t'和平均風速的邊緣分布函數。

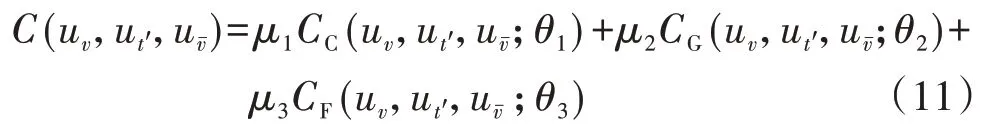
步驟⑤是通過式（6）、（7）、（11）獲得描述風電場瞬時風速的三元聯合密度函數。

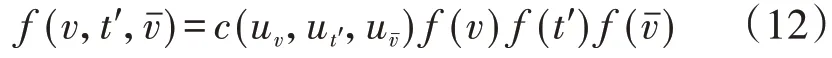
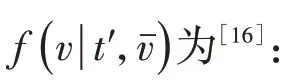
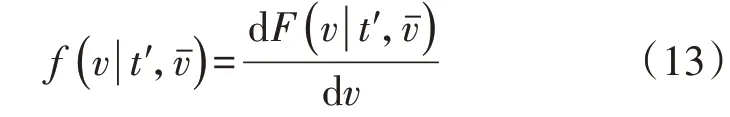
2 可用慣量評估方法

針對風機實時運行中的可用慣量，本節以雙饋風電機組DFIG（Doubly-Fed Induction Generator）虛擬慣量控制為基礎，分析全風況下的風機轉速變化情況，構建單臺風機以及全風電場的可用慣量的概率模型，并獲得一定置信度下全風電場可用慣量置信區間。

2.1 虛擬慣量控制

目前，通過施加控制環節可使風機在面臨頻率事故時能如同同步機釋放或吸收風機轉動部分的旋轉動能，將這種控制方式稱為虛擬慣量控制，控制框圖見附錄A圖A2。通常，風機存儲的可用慣量E為：其中，ω 為風機正常運行時的轉子轉速；J 為包含發電機轉子、葉輪等多種轉動結構的總轉動慣量。

從功率角度出發，對存儲在雙饋風電機組旋轉轉子以及相關耦合旋轉部件中的慣性動能求導可獲得風機實時可提供的慣性功率支撐ΔP為：

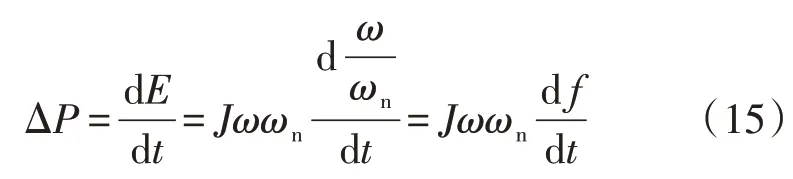
其中，ωn為風機的額定轉速；f 為電網頻率。

2.2 全風況下風機轉子轉速

雙饋風電機組運行狀況如圖2 所示，風機狀態分為啟動區（SⅡ?1）、MPPT 區（SⅡ?2）、恒轉速區（SⅢ）、恒功率區（SⅣ）和切出風速區（SV）。圖中，ωmin、ωs、ωmax分別為風機的最低并網轉速、恒轉速區轉速和最高轉速；P 為風機輸出功率；Pmax為輸出功率最大值；vmin、、vωs、vn、vmax分別為切入風速、調頻退出風速、恒轉速區風速下限、額定風速和切出風速。

圖2 全風況下雙饋風電機組運行工況Fig.2 Operational condition of DFIG under full wind speed condition

SⅠ、SⅡ?1和SV區：受風速狀況限制，風機無法正常并網運行或無轉速下降能力，因而，在該風速區內風電機組不參與電力系統頻率響應，無可用慣量。

SⅡ?2區：在中低風速下，通過風機MPPT 控制可以使得風機正常運行時的輸出功率在輸出曲線的最高點。風機捕獲的機械功率Pm如式（16）所示［7］。

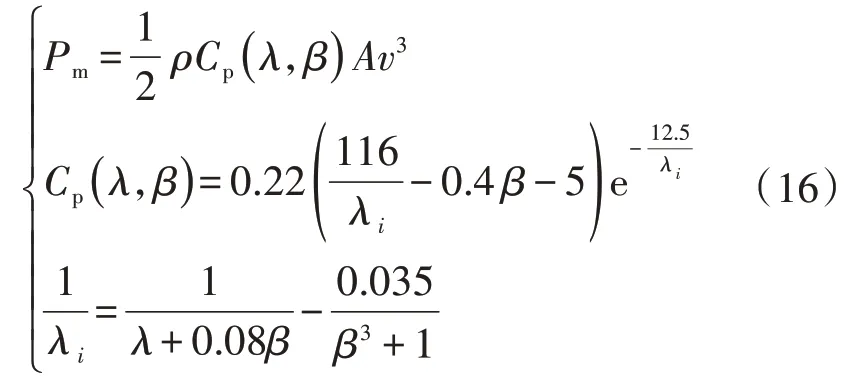
其中，ρ為空氣密度；Cp為風能轉換效率；λ為葉尖速比，定義為λ=ωtR/v，ωt為風機葉輪旋轉角速度，R為葉輪半徑；β為槳距角；A為風機掃風面積；λi為Cp與槳距角β的中間變量。

風機工作在SⅡ?2區時，風能轉換效率最大，此時，槳距角β=0，同時，風機運行滿足：

通過上式求得最優葉尖速比λopt，由最優葉尖速比的定義可得到線性化的風機轉速-風速關系式為：

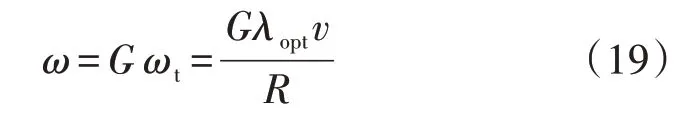
其中，G為風機齒輪箱傳遞系數。

SⅢ區：處于恒轉速區的風機轉速隨風速增加變化較小，但此時風機的捕獲功率仍呈現上升趨勢。根據文獻［17-18］提出的風機功率曲線關系，可推得近似線性化轉速方程如式（20）所示，關系式記為uⅢ(v)。

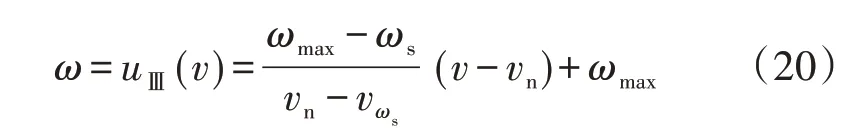
SⅣ區：當風速超過vn后，風機輸出功率將不會繼續增加，轉子轉速達到最高轉速。

2.3 可用慣量評估方法

風電場內可用慣量的影響因素主要包含風電場風況和風機運行工況兩方面。風況已通過第1 節風速模型進行了描述，本節將在單臺風機可用慣量評估算法中引入風機運行工況，主要考慮運行過程中風電場機組的慣量控制策略狀況以及風機自身的故障情況。

由2.2 節可知，當風機處于MPPT 運行時，轉速隨風速變化將處于不同的區域。考慮尾流影響時，風電場內不同轉速區風機的可用慣量因風速狀況不同存在較大的差異。對于單臺雙饋風電機組，其轉動機構中存儲的旋轉動能在慣量響應過程中無法全部釋放，轉子轉速存在最低轉速ωmin（0.7 p.u.）。因而，若風機j實際轉速為ωj，則其可用慣量Ej為：

由圖2 可以看出，啟動區和切出風速狀態下，風機均無法參與調頻；中低風速狀態下，風機能保持MPPT 狀態運行；當風速高于調頻退出風速時，風機才具備慣量響應能力；達到額定風速后，風機轉速保持不變，可用慣量為確定值。綜上，全風況下風機j的可用慣量按風速狀況可分為式（23）所示4個階段。

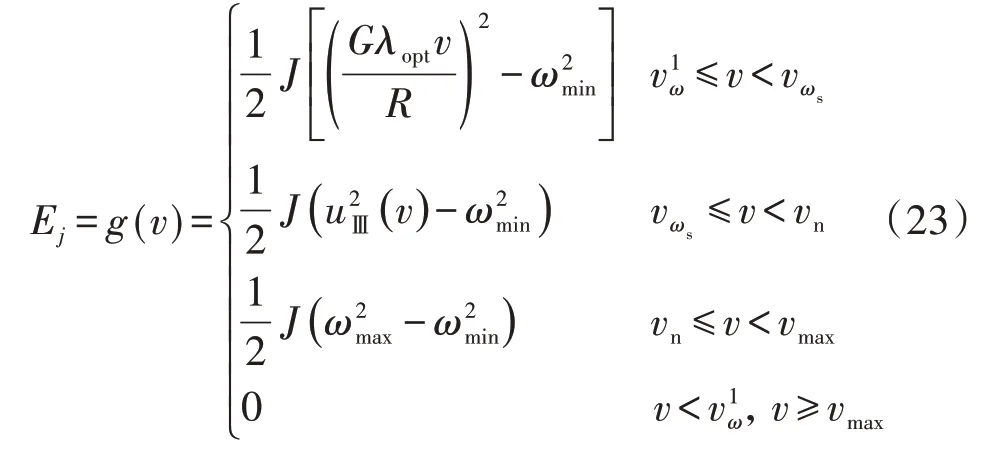
結合式（15）和式（19）—（23），從慣性功率增量出發，虛擬慣量控制下風機j 的可用慣性功率增量Pj為：

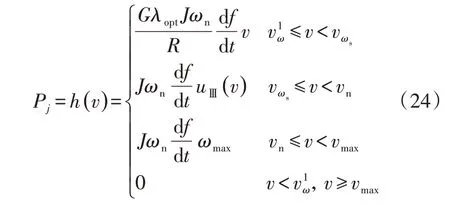
當忽略機組運行狀態時，單風機的可用慣量由風速決定。同時，由1.5 節可知，風機j 在慣性響應內的風速可由函數描述。因而，結合隨機變量反函數概率密度理論，實時運行中風機j 的可用慣量的概率密度函數fj(Ej)和可用慣性功率增量的概率密度函數fj(Pj)分別為：

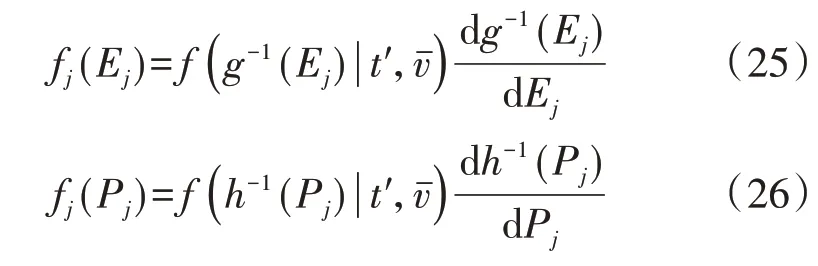
假設由風機統計數據得到風機j 的故障率為pj，則從能量角度出發，風機j 可用慣量的概率密度函數f(Ej)為：

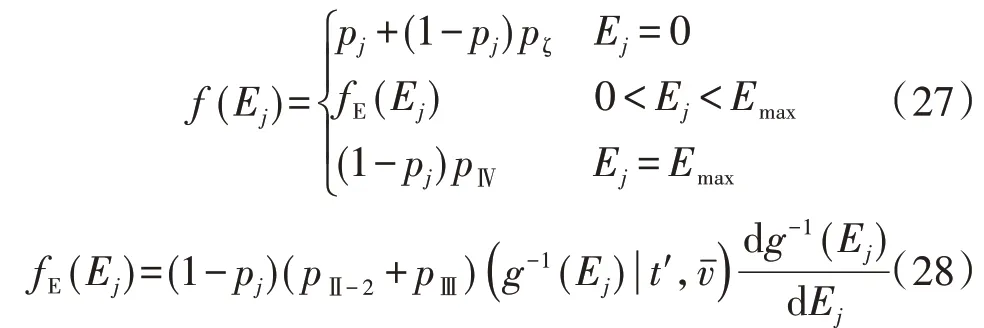
其中，pⅣ、pⅡ?2、pⅢ分別為風機運行在圖2 中風速區SⅣ、SⅡ?2、SⅢ的概率值；pζ為風機處于無可用慣量風速區的概率，pζ=pⅠ+pⅡ?1+pV。對于任意風速區Sx(x=Ⅰ ，Ⅱ?1，Ⅱ?2，Ⅲ，Ⅳ，Ⅴ)，風機運行概率值px的表達式為：

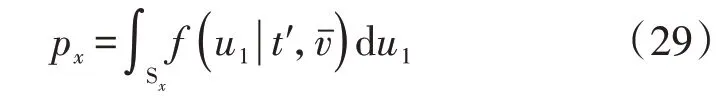
可以看出，單臺風機的可用慣量可分為無可用慣量、恒定可用慣量和變化可用慣量3 種狀態。從功率增量角度出發，可用慣量的分布情況為：

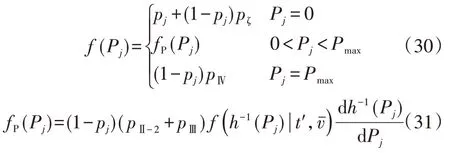
2.4 可用慣量置信區間

風電場內各風機間主要存在尾流效應影響下的風速聯系，對于風速分布已知的情況，在進行算法的區間估計時各風機可用慣量按獨立隨機變量處理。基于所提可用慣量概率評估模型，風電場可用慣量置信區間的獲取步驟如下。

對于需求方，在中國經濟快速發展這個大環境下，物價也隨之提高，各大企業更是坐地起價。而共享經濟為需求方提供的服務，往往低于市場企業價格，這時選擇共享經濟下的商品和服務，對于需求者來說是有利的。以首都北京為例，在非高峰期的時段打車走十公里的路程，需要花費四十分鐘的時間成本和34元的人民幣資金成本。現在共享經濟下推行的滴滴打車卻只要二十五元人民幣，在這種情況下，共享經濟帶來的優惠就成為了需求方的額外收益。

（1）求得風電場實時運行中每臺風電機組可用慣量的概率密度函數f(E)和f(P)。

（2）對f(E)和f(P)進行積分獲得可用慣量的概率分布函數?(E)和?(P)。

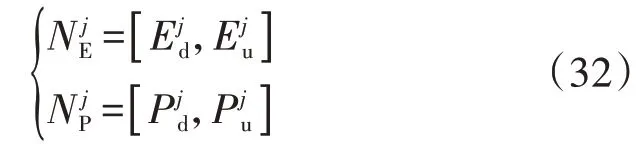
（4）將風電場各風機可用慣量疊加求得全風電場的可用慣量的置信區間，若風電場風機總數為N，則全風電場可用慣量和可用慣性功率增量區間NE和NP分別為：

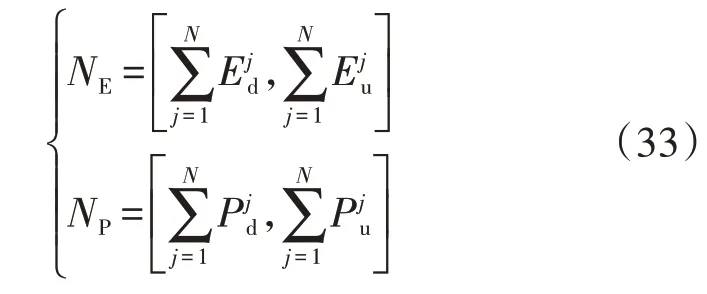
3 算例及仿真

以西北某風電場M 為例，場內風機布置示意圖如附錄A 圖A3 所示。采用風電場M 實測風速數據進行單風電場可用慣量的評估。進行風機風速建模時，選取風速基準高度h0=10 m，風剪切效應系數σ=0.2，風機間距X=50 m，時間延遲τ與風機間間距和風速相關，近似關系認為τ≈X/v；評估模型中，假定風機故障概率pj=0.05，風機參數見附錄C表C1。

3.1 評估算法對比

（1）與常規Copula函數評估結果比較。

本文選取阿基米德族的Gumbel-Copula函數（分布函數圖見附錄A 圖A4）構建評估模型，并將所提方法與該方法的評估結果進行比較。假定系統出現負荷突增，電網頻率跌落，可用慣量評估的置信度取為90%。選取8～16 m／s 間5 組典型風速對風電場內單風機可用慣量進行評估，結果如圖3所示。

由圖3 可知，風速增大時，Gumbel-Copula 法的可用慣量置信區間呈現先增大后減小的趨勢，而混合Copula法的置信區間不斷增大，且在各風速下，尤其在低風速和高風速下，混合Copula 法結果均保持較大的區間裕度，能夠更好地適應風速變化，提供更為可靠的風機可用慣量情況。

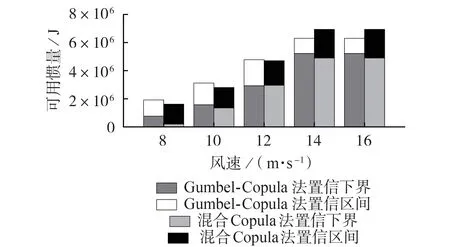
圖3 混合Copula和Gumbel-Copula法評估結果Fig.3 Evaluation results of mixed Copula and Gumbel-Copula methods

風電場評估中的標稱算法是指忽略場內各風電機組間的差異，通過單機等值化處理等效全風電場。本文分別采用所提方法與標稱算法對風電場可用慣量進行評估。設定不同的風電場場端平均風速評估全風電場的可用慣量區間，評估結果如圖4所示。

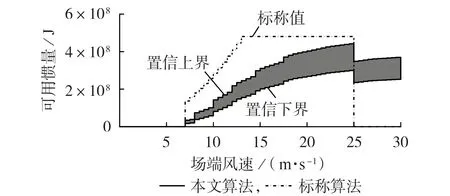
圖4 90%置信度下風電場可用慣量-場端風速曲線Fig.4 Available inertia of wind farm vs. speed of wind farm terminal with 90% confidence level

由圖4 可知：低風速下，風機轉速較低，無調頻裕度；中高風速下，風電場可用慣量隨風速升高而增加，且標稱值始終高于所提方法結果；額定風速后，前排機組轉速不變，但由于尾流存在，后排機組可用慣量繼續增加，而標稱算法下的機組均被視為恒轉速運行，風電場可用慣量恒定，所得結果誤差偏高。

當達到切出風速后，標稱算法的評估曲線降至0，但當實時風速突變到超出切出風速時，前排風電機組將退出運行，但尾流影響下的后排機組仍具有慣量響應能力，風電場總的可用慣量驟降。

綜上，與標稱算法相比，所提方法可有效減少估算結果與實際值之間的誤差。

3.2 實時評估曲線

（1）可用慣量和功率增量曲線。

實時運行時，以風電場M 夏季某日06:00—12:00 風速數據進行可用慣量評估。從能量和功率的角度分析，整個風電場慣量變化曲線如圖5所示。

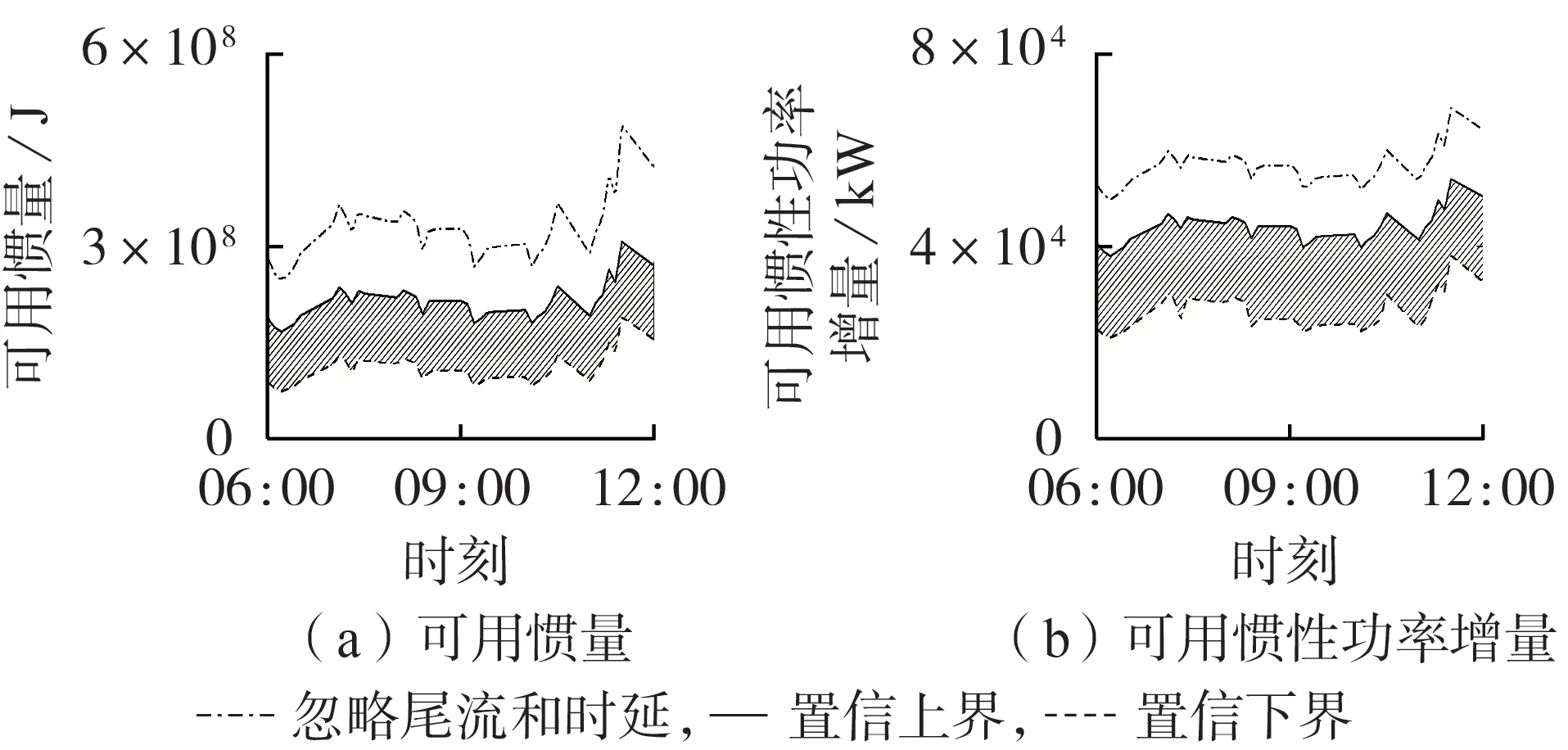
圖5 置信度為90%時的風電場評估曲線Fig.5 Evaluation curves of wind farm with 90% confidence level

風電場任意時刻的可用慣量真實值在圖中陰影部分中。風電場大部分風機運行在MPPT 區和恒轉速區，評估曲線跟隨實時風速同步變化，可提供直觀的風電場可用慣量時變情況。此外，風電場風機的可用慣量和短時可增發的有功功率實時評估曲線基本一致，均能直觀描述風電場可用慣量的變化。

（2）不同置信度下的評估結果。

多種置信度下的評估結果能夠突出風電場可用慣量的裕度大小。選取不同置信度得到風電場可用慣量曲線如圖6所示。

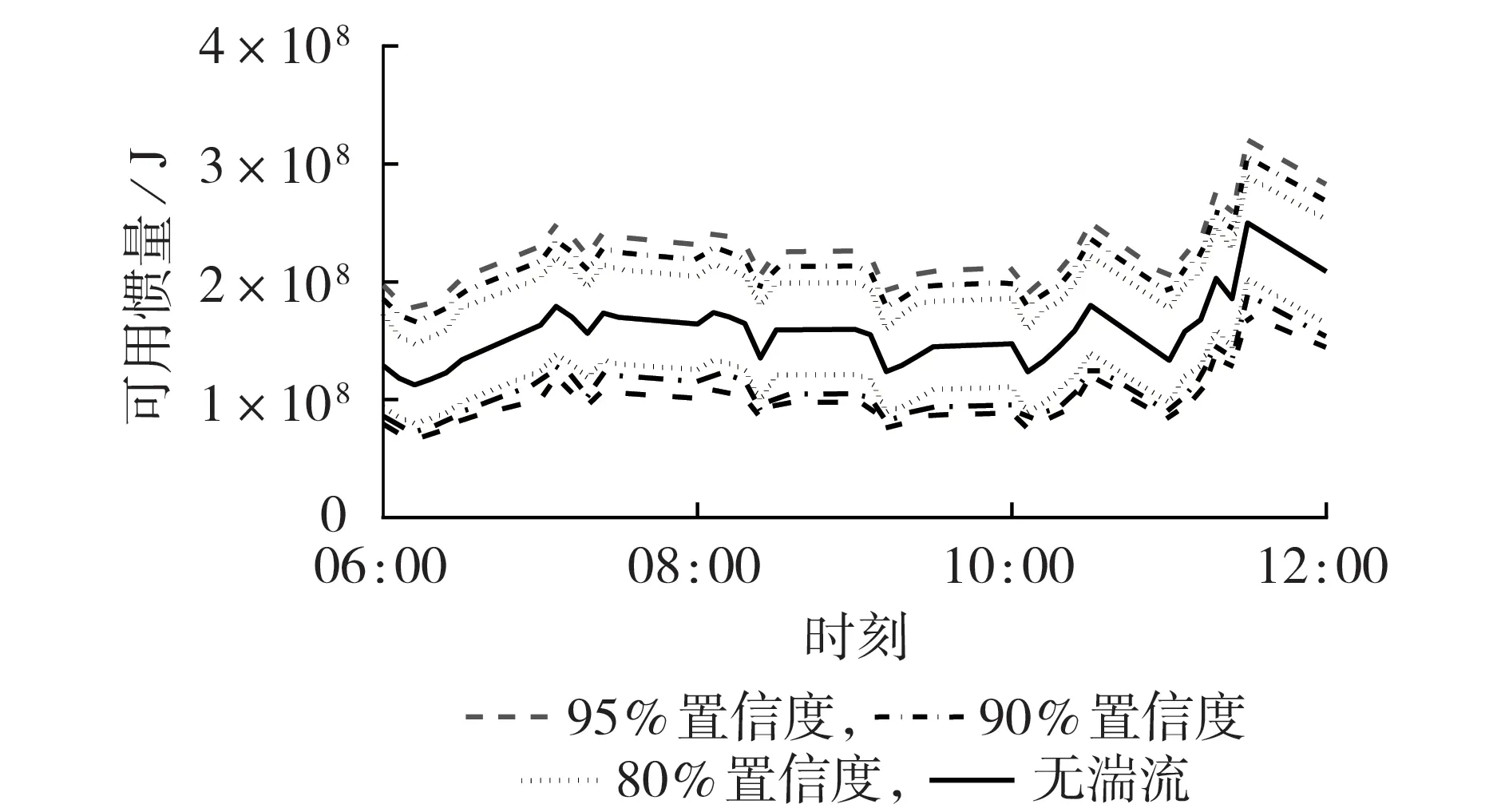
圖6 不同置信度下的風電場可用慣量評估曲線Fig.6 Available inertia evaluation curves of wind farm under different confidence levels

由圖6 可知，考慮大氣湍流下各置信度的可用慣量評估曲線與無湍流下的曲線保持同步變化趨勢。隨著置信度的提高，置信區間不斷增大，即評估風險減小，但相應算法的結果波動范圍變大。因此，當決策者制定調頻方案時，可根據實時電網的運行情況以及各風電場不同置信度下的可用慣量評估曲線來制定各類風險性下的最優調頻控制方案。

3.3 置信區間評估方式有效性驗證

在Simulink 平臺搭建等效風電場模型，通過風電場仿真驗證算法的有效性，風電場接線圖和仿真參數見附錄A圖A5和附錄C表C2。

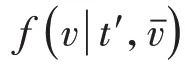
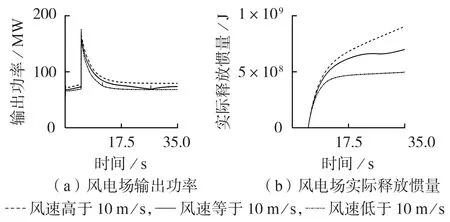
圖7 風電場慣量響應仿真曲線Fig.7 Simulative curves of wind farm inertia response

由圖7 可以看出，場端風速越大，2 類曲線對應值越大。在功率曲線上，5 s 時調頻控制動作，風機轉速降低釋放可用慣量，輸出功率出現突增現象，由于后續有功參考值不斷下降，風機的功率曲線也呈下降趨勢。慣量釋放曲線在5 s 前恒定為0，5 s 后則不斷上升。

當考慮湍流影響時，通過所提方法進行評估，可以得到估算的可用慣量置信區間，與Gumbel-Copula法進行比較，本文所提方法結果超出置信區間上、下界仿真組數及誤差情況如表1 所示。由表中可知，在3 種典型置信度下，所提方法評估結果誤差率均達到置信度要求，越上限和越下限的情況均在允許范圍內，且評估所得置信下界效果更優。相比之下，Gumbel-Copula 法在置信度較高時誤差較小，但置信度降低時評估誤差超出置信度要求。綜上，所提方法能較好地評估風電場實時運行中的慣性響應能力。

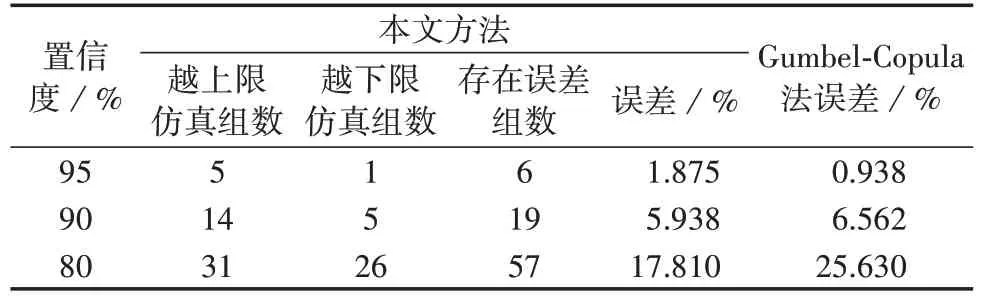
表1 不同置信度下本文方法評估結果誤差Table 1 Evaluation error of proposed method under different confidence levels

4 結論

本文針對風電場參與調頻服務時慣性響應能力缺乏準確估計的問題，提出一種考慮風電場風速分布和風機運行工況的風電場可用慣量概率化評估方法。分別從能量和功率2 個方面，獲得一定置信度下的風電場可用慣量和可用慣性功率增量評估曲線。以西北某實際風電場的結構和風速數據對本文所提評估方法進行算例分析。對比分析可知，所提方法能有效減少估算誤差，對電力系統運行調度具有較強的參考性和指導性。同時，利用Simulink 搭建等效風電場模型進行仿真驗證，統計結果表明本文所提的置信區間評估結果誤差較小，具有較高的可信度。

附錄見本刊網絡版（http：//www.epae.cn）。