混合雙饋入直流輸電系統控制回路間交互影響定量分析

張 芳，楊中堯

（天津大學 智能電網教育部重點實驗室，天津300072）

0 引言

基于電網換相換流器（LCC）的高壓直流（LCCHVDC）輸電系統被廣泛應用于遠距離大容量輸電場合，基于電壓源型換流器的高壓直流（VSCHVDC）輸電系統因其在可控性方面的優勢，在海上風電場并網等領域也已進入大規模應用階段［1］。隨著各種直流工程的建設，將很可能出現LCC-HVDC饋入交流母線與VSC-HVDC饋入交流母線間電氣距離較近的情況，由此構成混合多饋入直流輸電系統。

在混合多饋入直流輸電系統的逆變側，LCCHVDC 與VSC-HVDC 間不可避免地產生交互影響。為了有效評估該交互影響，國內外學者進行了一系列研究：文獻［2-3］提出了基于運行阻抗的等值有效短路比指標，揭示了影響2 種直流系統間交互作用程度的因素；文獻［4-5］從LCC-HVDC 功率輸送極限提升的角度，提出了視在短路比增加量指標，突出了引入VSC-HVDC對LCC-HVDC最大傳輸功率的提升作用；文獻［6］提出了VSC-HVDC 不同控制方式下，LCC-HVDC 受端電壓支撐強度因子的解析計算方法，有效反映了VSC-HVDC 對LCC-HVDC 受端系統強度的影響；文獻［7］將除LCC-HVDC以外的系統進行等值，提出了等值電壓穩定因子的計算方法，可對其換相失敗免疫水平進行快速評估；文獻［8］通過綜合考慮各項穩定約束得到了VSC-HVDC的穩態運行區域，并基于此分析了LCC-HVDC 采取不同控制策略和運行方式對VSC-HVDC的影響；文獻［9］從全局穩定性角度出發，利用特征值分析法研究了混合雙饋入直流輸電系統中參數選取對系統小擾動穩定性的影響；文獻［10］將混合雙饋入直流輸電系統等效為單輸入單輸出系統，利用奈奎斯特穩定性判據研究了各控制器參數對系統穩定裕度的影響。

為進一步明確混合多饋入直流輸電系統內部交互作用產生的原因，本文以混合雙饋入直流輸電系統為例，從控制回路間耦合的角度進行研究。首先，將混合雙饋入直流輸電系統等效為多輸入多輸出（MIMO）系統，構建了混合雙饋入直流輸電系統的傳遞函數；隨后利用分析MIMO 系統交互作用的有效工具——相對增益矩陣RGA（Relative Gain Array）方法［11-13］進行研究，定量評估了受端交流系統強度、聯絡線長度、直流功率傳輸水平以及直流系統功率振蕩頻率等因素對LCC-HVDC和VSC-HVDC交互作用的影響；最后，利用電磁暫態仿真對分析結果的有效性進行驗證。本文的研究基礎是系統在穩態平衡點附近的小信號模型，因此對換相失敗等暫態過程的分析不在考慮范圍之內。

現有文獻對混合雙饋入直流輸電系統內部交互作用的研究大多從交流系統強度以及系統穩定性等方面進行考慮，而本文與上述研究的不同之處在于：分析混合雙饋入直流輸電系統內部控制回路間耦合程度對控制效果的影響。由RGA 中的元素數值得到控制回路間耦合程度的定量指標，據此對影響系統控制回路間耦合程度的多種要素進行分析，為混合雙饋入直流輸電系統中交互作用的分析提供了新的視角和思路。

1 混合雙饋入直流輸電系統模型

本文研究的混合雙饋入直流輸電系統如圖1 所示。圖中，Pdci+jQdci（i=1，2）為直流系統通過交流母線i 注入交流系統的復功率；Uti∠δti為交流母線i 的電壓相量；Us1∠0°、Us2∠δs2為交流系統等效電源相量；Zsi、θsi分別為與交流母線i 相連的交流系統等效阻抗及其阻抗角；Isi為由交流母線i流入與其相連交流系統的電流相量；Ps3+jQs3為交流母線1、2 間聯絡線上流經的復功率；Zs3、θs3分別為聯絡線阻抗及其阻抗角；Zc、θc分別為LCC-HVDC 逆變側濾波器的阻抗及其阻抗角；Pc+jQc為LCC-HVDC 逆變側濾波器注入交流系統的復功率。

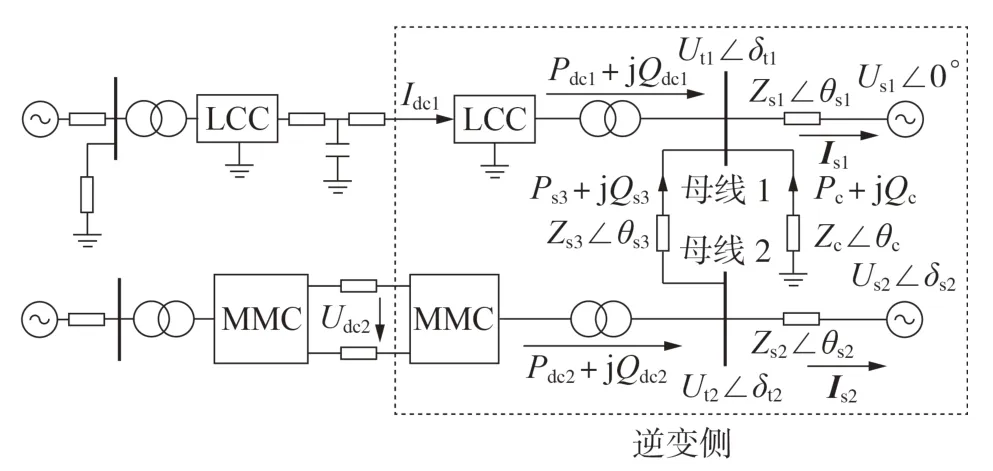
圖1 混合雙饋入直流輸電系統結構Fig.1 Structure of hybrid dual-infeed HVDC system

由 圖1 可 知，LCC-HVDC 和VSC-HVDC 分 別 通過2 條電氣距離較近的交流母線饋入受端交流系統。VSC-HVDC采用模塊化多電平換流器（MMC）拓撲結構。限于篇幅，本文僅針對采用以下控制方式的混合雙饋入直流輸電系統進行分析：LCC-HVDC整流側采用定直流電流控制，逆變側采用定關斷角控制；MMC-HVDC 整流側采用定直流電壓、定無功控制，逆變側采用定有功、定交流電壓控制。圖中LCC-HVDC 逆變側換流站與MMC-HVDC 逆變側換流站電氣距離較近，本文重點研究逆變側2 座換流站之間的交互作用。由此作出以下假設：LCCHVDC整流側定直流電流控制器可使直流電流Idc1保持恒定；MMC-HVDC 整流側定直流電壓控制器可使直流電壓Udc2保持恒定。

2 混合雙饋入直流輸電系統RGA構建

2.1 RGA原理

RGA 方法可用來分析MIMO 系統中輸入變量對輸出變量的影響程度，常據此得出輸入變量和輸出變量的最佳匹配關系。對于給定MIMO 系統，設其傳遞函數矩陣為G（s），輸入變量uj對輸出變量yh的影響程度可用相對增益λhj表示［11］，即：

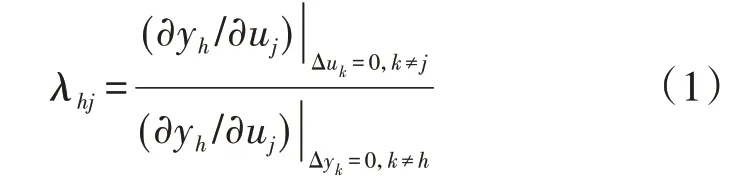
其中，分子為除uj→yh控制回路外其余回路均開環時輸入變量uj對輸出變量yh的增益，此時除uj以外的其余輸入變量uk（k≠j）均保持不變，即uk變化量Δuk=0；分母為除uj→yh控制回路外其余回路均閉環且理想控制時輸入變量uj對輸出變量yh的增益，此時除yh以外的其余輸出變量yk（k≠h）均保持不變，即yk變化量Δyk=0。

式（1）也可寫成式（2）所示形式：為G-1（s）中的元素g'jh。

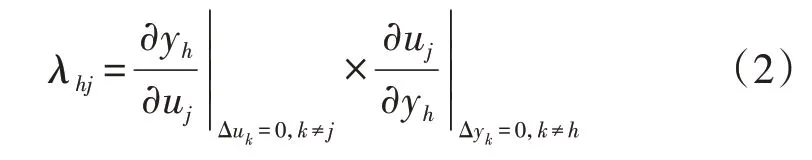
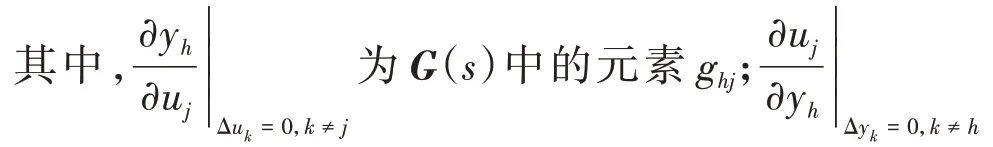
由此，若給定的MIMO 系統為方陣，由相對增益λhj構成的RGA為：

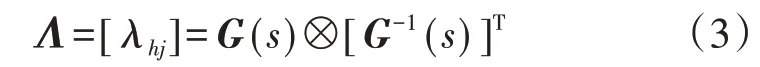
其中，“?”表示2 個矩陣的Hadamard 乘積。當s=0時，可得系統穩態情況下的RGA；當s=jω=j2π f（ω、f 分別為系統角頻率和頻率）時，可得被控系統在特定頻率下的RGA，其可反映系統在不同頻率正弦信號輸入下的耦合特性［14］。

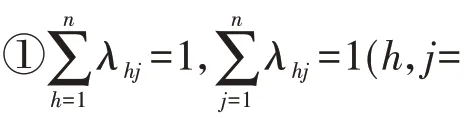
2.2 混合雙饋入直流輸電系統RGA構建

對于本文所研究的混合雙饋入直流輸電系統，其可構成圖2所示的MIMO系統。圖中，w（s）為被控系統傳遞函數G（s）的輸出變量，包括LCC 關斷角γ、MMC 輸送有功Pdc2和MMC 受端交流電壓Ut2；u（s）為被控系統G（s）的控制變量，由LCC 定關斷角控制器輸出變量β 和MMC 定有功、定交流電壓控制器輸出變量Idref、Iqref構成，被控系統傳遞函數G（s）可由下文混合雙饋入直流輸電系統逆變側小信號模型推導得出；ic2d、ic2q分別為MMC 注入交流系統電流ic2的d、q軸分量；ut2d、ut2q分別為MMC 受端交流電壓Ut2的d、q軸分量；uad、uaq分別為MMC等效內電勢ua的d、q軸分量；“Δ”表示對應變量的小信號量。

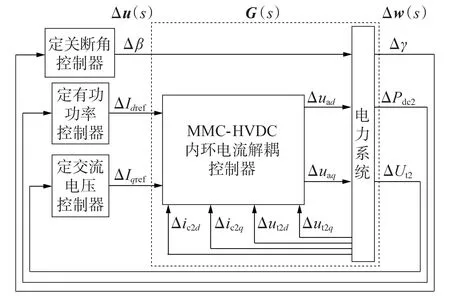
圖2 混合雙饋入直流輸電系統逆變側控制框圖Fig.2 Control block diagram of inverter-side of hybrid dual-infeed HVDC system

將附錄A 式（A1）—（A12）組成的被控系統狀態空間模型在穩態平衡點處線性化，可得被控系統的小信號模型為：

其中，x 為被控系統相關狀態變量，維數為32×1，其具體含義見附錄A表A1；w=［γ Pdc2Ut2］T為被控系統的輸出變量；u=［β IdrefIqref］T為被控系統的控制變量；A、B、C、D 分別為系統狀態矩陣、輸入矩陣、輸出矩陣和前饋矩陣。

通過對式（4）進行拉普拉斯變換可得混合雙饋入直流輸電系統逆變側被控系統的傳遞函數為［15］：

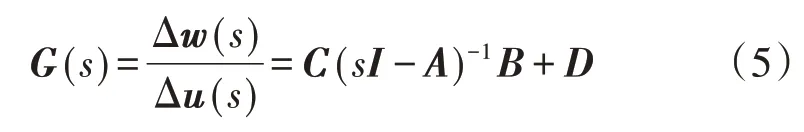
其中，I為單位對角陣。

將G（s）代入式（3），可得被控系統的RGA為：

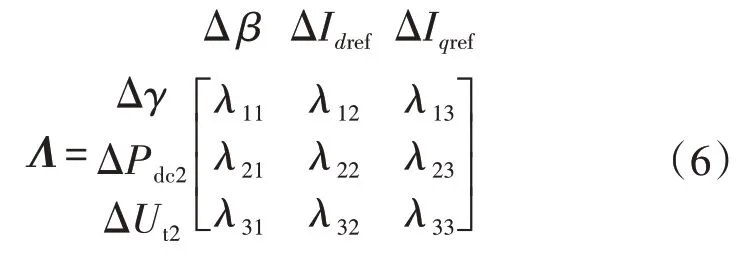
3 混合雙饋入直流輸電系統控制回路間交互影響分析

3.1 基于RGA 的混合雙饋入直流輸電系統內部交互影響分析方法

采用RGA 對混合雙饋入直流輸電系統內部交互影響的分析方法如下：①在給定參數確立的穩態平衡點附近構建形如式（4）所示的被控系統小信號模型；②依據所建立的小信號模型推導被控系統傳遞函數G（s），進而利用式（3）計算系統的RGA；③結合2.1 節中RGA 的基本特性對混合雙饋入直流輸電系統逆變側3 個控制回路間耦合作用程度進行定量分析。值得注意的是，本文所做分析均基于穩態平衡點附近的小信號模型，因此當系統運行參數發生改變時，需在新的穩態平衡點重新進行模型線性化以及傳遞函數和RGA計算。

3.2 參數設置及分析驗證

在PSCAD／EMTDC 仿真平臺中搭建如圖1 所示的混合雙饋入直流輸電系統模型。系統的基準功率為1000 MW，聯絡線參數為R0=0.079 Ω／km、X0=0.405 Ω／km，LCC-HVDC 采用CIGRE 標準測試模型［16］，其他參數見附錄B表B1和表B2。

根據3.1節方法定量分析受端交流系統強度、聯絡線長度、直流功率傳輸水平以及直流系統功率振蕩頻率對混合雙饋入直流輸電系統內部的交互影響。本文參考文獻［9］中方法，采用聯絡線斷開時計算的短路比kSCRi來衡量與交流母線i 相連的交流系統強度，其表達式為：

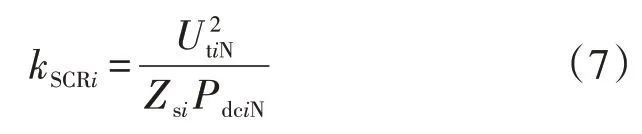
其中，UtiN為交流母線i 的額定電壓；PdciN為與交流母線i相連直流系統的額定功率。

3.2.1 受端交流系統強度

交流系統強度是影響直流系統穩定運行的重要因素，因此本節針對交流系統短路比對混合雙饋入直流輸電系統控制回路間耦合程度的影響進行研究。設聯絡線長度L=0（2個直流系統饋入同一條交流母線），不同kSCR下系統穩態RGA分別為：

由式（8）—（10）可知，隨著kSCR的增大，λ11、λ22、λ33均逐漸增大，其與1 的距離逐漸減小，而λ12與λ21均近似為0。由RGA 基本特性可知，在受端交流系統強度變化過程中，對于系統逆變側，LCC 控制回路與MMC 有功控制回路間基本無交互影響，LCC 與MMC 間的耦合作用主要存在于LCC 控制回路與MMC 無功控制回路之間。λ13與λ31隨受端交流系統短路比的增大而減小，LCC 控制回路與MMC 無功控制回路之間的耦合程度隨受端交流系統強度的增強而減弱。由LCC 控制回路與MMC 無功控制回路的調節過程可知，2 個控制回路均受饋入交流母線電壓波動的影響，單個控制回路的調節作用可由饋入交流母線電壓的波動影響另一控制回路的調節過程，受端交流系統強度越強，其對饋入母線電壓的支撐能力越強，饋入母線電壓的波動越小，LCC 控制回路和MMC 無功控制回路間的交互影響程度越小。隨著kSCR的增大，λ22由0.8726變化至1.004 9，其與1 的距離逐漸減小，而λ23逐漸減小。則根據RGA基本特性，在受端交流系統較弱時，對于系統逆變側，MMC有功、無功控制回路間存在一定的耦合作用，增強受端交流系統強度后，MMC 有功、無功控制回路間耦合程度降低，當受端系統為強交流系統時，MMC 控制回路才滿足有功、無功解耦控制的設計初衷，與文獻［17］所得結論一致。

3.2.2 聯絡線長度

在直流系統工程規劃過程中，換流站間的電氣距離對電力系統的影響是換流站站址選擇的重要參考，因此本節針對聯絡線長度對混合雙饋入直流輸電系統控制回路間耦合程度的影響進行研究。設kSCR=1.5，不同聯絡線長度L下系統穩態RGA分別為：

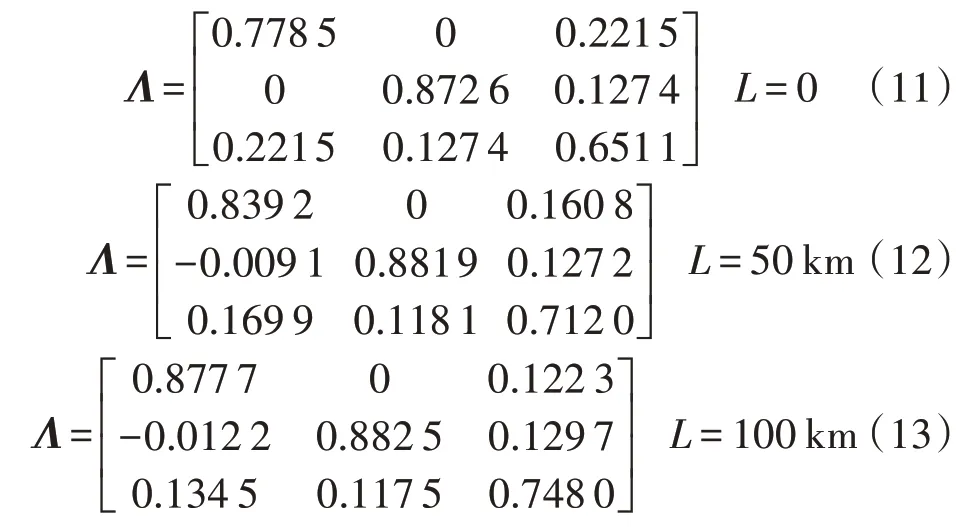
由式（11）—（13）可知，隨著L 的增大，λ11、λ22、λ33均逐漸增大，其與1 的距離逐漸減小，且λ12與λ21均近似為0。由RGA 基本特性可知，在聯絡線長度變化過程中，對于系統逆變側，LCC 控制回路與MMC有功控制回路間基本無交互影響，LCC與MMC控制回路間的耦合作用主要存在于LCC控制回路與MMC 無功控制回路之間，其耦合程度隨聯絡線長度的增加而減弱。由3.2.1 節分析可知，LCC 控制回路與MMC 無功控制回路間的耦合作用經饋入交流母線的電壓波動傳遞，聯絡線長度越長，母線1、2 間的電氣距離越遠，母線1電壓受母線2電壓的波動影響越小，LCC 控制回路和MMC 無功控制回路間耦合作用越小，與文獻［3］結論一致。隨著L 的增大，相較于λ11和λ33的變化幅度，λ22變化幅度很小，并且λ12與λ21均近似為0。由RGA 基本特性可知，在受端交流系統較弱時，對于系統逆變側，MMC 有功、無功控制回路間的耦合作用受聯絡線長度變化的影響較小。

3.2.3 直流功率傳輸水平

實際運行的直流工程在參與電網穩定控制時，需對直流功率進行調制，因此本節研究了不同直流功率傳輸水平對混合雙饋入直流輸電系統控制回路間耦合程度的影響。設kSCR=1.5，L=0，Pdc1=1 000 MW，不同Pdc2下系統的穩態RGA分別為：

由式（14）—（16）可知，隨著Pdc2的降低，λ11、λ13基本保持不變，并且λ12近似為0。由RGA 基本特性可知，在系統逆變側，LCC 控制回路與MMC 有功控制回路間基本無交互影響，LCC 與MMC 間的耦合作用主要存在于LCC 控制回路與MMC 無功控制回路之間，且其耦合程度基本不變。隨著Pdc2的降低，λ22由0.8726變化至0.9183，其與1的距離逐漸減小，而λ23逐漸減小。由RGA 基本特性可知，在系統逆變側，MMC 有功、無功控制回路間的耦合作用逐漸減弱。

當Pdc2=400 MW 時，不同Pdc1下系統的穩態RGA分別見附錄C式（C1）—（C3），分析過程見附錄C。

3.2.4 直流系統功率振蕩頻率

由2.1 節可知，當s=jω=j2π f 時，可得被控系統在特定頻率下的RGA，其可反映系統在不同頻率正弦信號輸入下的耦合特性。在時域仿真驗證中被控系統頻率的正弦輸入信號由直流功率參考信號中附加正弦擾動產生。若系統的控制器參數已知，在穩態運行點附近各控制回路閉環傳遞函數的幅頻特性曲線及相應的帶寬頻率fWb1—fWb3如圖3所示。帶寬頻率表示閉環幅頻特性衰減到靜態增益的0.707（對應圖3中幅值為-3 dB）時所對應的頻率［14］。一方面，當正弦輸入信號的頻率高于帶寬頻率時，被控系統的幅值將呈現較大衰減；另一方面，帶寬頻率附近RGA的分析結果較為重要［14］。因此根據圖3 所示各控制回路的帶寬頻率，本文重點計算0～6 Hz內的RGA。

圖3 各控制回路閉環幅頻特性曲線及帶寬頻率Fig.3 Closed-loop amplitude-frequency characteristic curve and bandwidth of each control loop

設kSCR=1.5、L=50 km、Pdc1=900 MW、Pdc2=350 MW，不同頻率下RGA 中各元素的模值見附錄D 圖D1。由圖可知，對于系統逆變側，隨著頻率的提高，λ13與λ31逐漸增大，LCC控制回路與MMC無功控制回路間的耦合程度逐漸加強；隨著頻率的提高，λ23與λ32先增大后減小，因此MMC 有功、無功控制回路間的耦合程度先加強后減弱；在頻率變化過程中，λ12與λ21均近似為0，由此得出LCC 控制回路與MMC 有功控制回路間的耦合作用始終較弱；而λ13始終大于λ23，LCC 控制回路與MMC 無功控制回路間的耦合作用始終強于MMC 有功、無功控制回路間的耦合作用，在影響MMC 無功控制回路控制效果的因素中，LCC控制回路與MMC 無功控制回路間的耦合作用占主導地位。

4 時域仿真驗證

本節將從混合雙饋入直流輸電系統控制回路間的耦合作用存在性、受端交流系統強度和聯絡線長度、直流功率傳輸水平以及直流系統功率振蕩頻率這4 個方面進行仿真驗證，分析上述因素對混合雙饋入直流輸電系統控制回路間耦合程度的影響。

下面針對LCC-HVDC逆變側采用定關斷角控制方式，MMC-HVDC 逆變側采用定有功、定交流電壓控制方式的混合雙饋入直流輸電系統進行分析。限于篇幅，直流系統采用其他組合控制方式時的分析過程及結論見附錄E。

4.1 混合雙饋入直流輸電系統控制回路間的耦合作用存在性

受端交流系統較弱時，MMC 有功、無功控制回路間的耦合作用已在文獻［17］中得到驗證，在此不再贅述。為了驗證系統逆變側LCC 與MMC 間的耦合作用主要存在于LCC 控制回路與MMC 無功控制回路之間，當kSCR=1.5、L=0 時，設3.5 s 時γref由15°階躍至16°，在不同工況下進行階躍擾動仿真，仿真結果見圖4。所設置的3 種工況如下：Case 1 為MMC-HVDC 逆變側有功、無功控制回路均保持閉環狀態；Case 2 為MMC-HVDC 逆變側有功控制回路 在t=3.5 s 時開 環，即Idref為 常量；Case 3 為MMCHVDC 逆變側無功控制回路在t=3.5 s 時開環，即Iqref為常量。

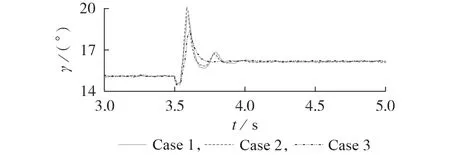
圖4 Case 1—3下的γ波形Fig.4 Waveforms of γ in Case 1-3

對比圖4中Case 1、2下的γ波形可知，階躍擾動發生后，在系統逆變側，γ 出現了較為明顯的振蕩現象，而MMC有功控制回路開環后，振蕩現象基本沒有改善。由此可得：MMC 有功控制回路閉環或開環對LCC 控制回路的控制效果影響很小，LCC 控制回路與MMC有功控制回路間基本無交互影響。對比圖中Case 1、3 下的γ 波形可知，MMC 無功控制回路開環后，γ的振蕩現象有所緩解。由此可得：MMC無功控制回路的閉環會削弱LCC控制回路的控制效果，LCC控制回路和MMC 無功控制回路間存在耦合作用。綜上，仿真結果驗證了3.2.1節理論分析的正確性。

4.2 受端交流系統強度和聯絡線長度

為了驗證混合雙饋入直流輸電系統控制回路間的耦合程度受交流系統強度和聯絡線長度的影響，在不同短路比和聯絡線長度下，當系統穩定運行后設t=3.5 s 時Ut2ref由1 p.u.階躍至0.97 p.u.，在不同工況下進行階躍擾動仿真，仿真結果見圖5（圖中Ut2、Pdc2為標幺值，后同）。Case 4—6 這3 種工況下的參數設置情況分別為kSCR=2.5、L=0；kSCR=1.5、L=0；kSCR=1.5、L=100 km。

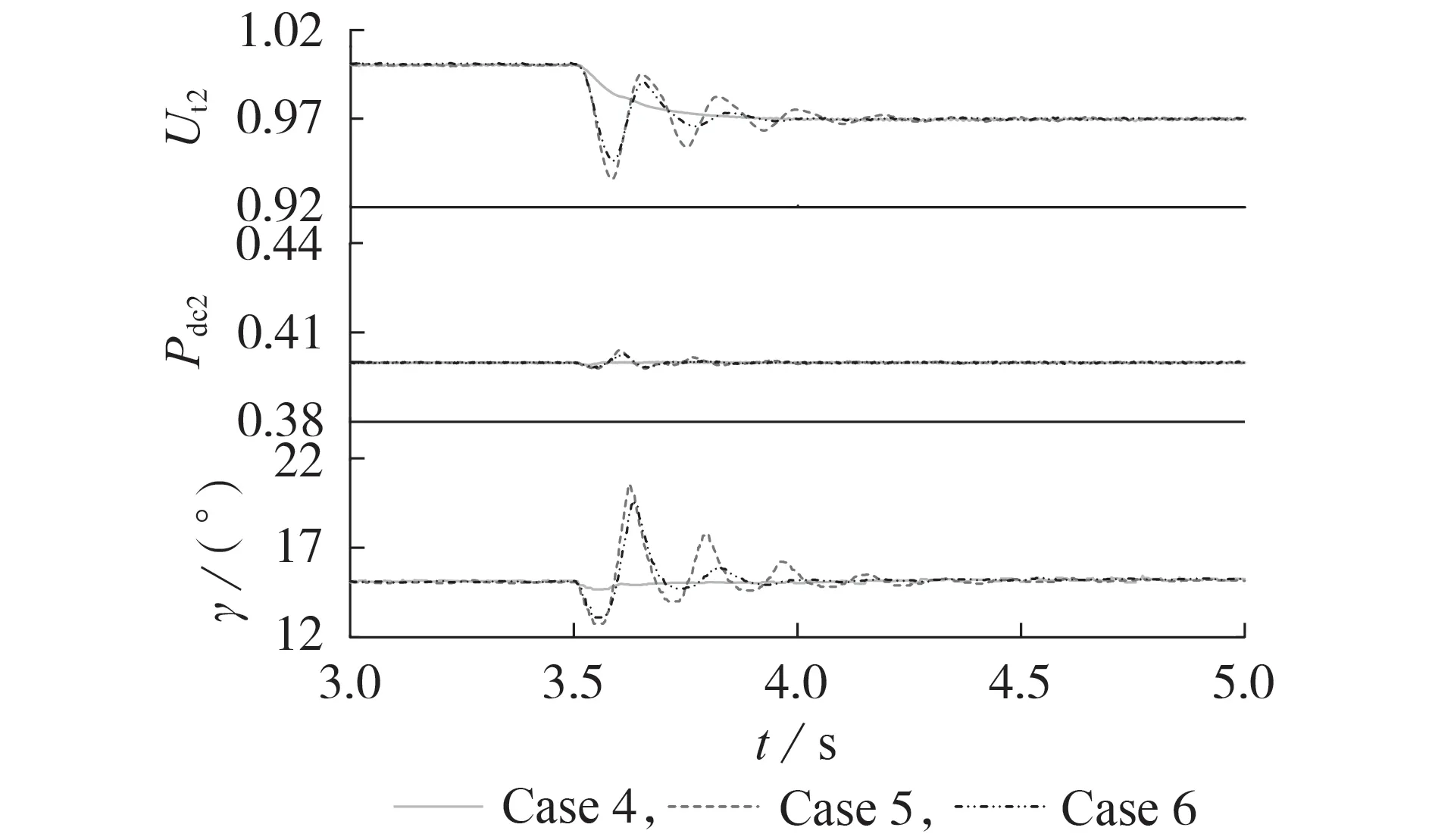
圖5 Case 4—6下的Ut2、Pdc2、γ波形Fig.5 Waveforms of Ut2，Pdc2 and γ in Case 4-6

對比圖5中Case 4、5下的γ波形可知，受端交流系統較強時，系統受到階躍擾動前后，γ 的動態響應特性幾乎無變化，而受端交流系統強度降低后，γ 出現了一定程度的振蕩現象，說明交流系統強度降低后，系統對交流母線電壓的支撐能力下降，LCC 控制回路與MMC 無功控制回路的耦合程度增強。對比圖5 中Case 4、5 下的Pdc2波形可知，受端交流系統較強時，系統受到階躍擾動前后，Pdc2的動態響應特性幾乎無變化，而受端交流系統強度降低后，Pdc2的動態響應特性出現輕微波動，說明交流系統強度降低后，在系統逆變側，MMC 有功、無功控制回路間的耦合程度增強。

對比圖中Case 5、6下的γ波形可知，聯絡線長度較長時，階躍擾動發生后，γ 的振蕩幅度與振蕩持續時間均較小，說明聯絡線長度較長時，母線1、2 間電氣距離較長，在系統逆變側，LCC控制回路與MMC無功控制回路間的耦合程度較弱。對比圖中Case 5、6下的Pdc2波形可知，聯絡線長度改變前后，系統受到相同階躍擾動，Pdc2的動態響應特性均只出現了輕微波動，說明系統逆變側MMC 有功、無功控制回路間的耦合作用受聯絡線長度變化的影響很小。綜上，仿真結果驗證了3.2.1節、3.2.2節理論分析的正確性。

4.3 直流功率傳輸水平

為了驗證混合雙饋入直流輸電系統控制回路間的耦合程度受系統運行方式的影響，當kSCR=1.5、L=0時，設3.5 s時Ut2ref由1 p.u.階躍至0.97 p.u.，針對混合雙饋入直流輸電系統不同功率傳輸水平的情況進行階躍擾動仿真，仿真結果見圖6。Case 7—9這3種工況下Pdc1均為1000 MW，Pdc2分別為400、350、300 MW。

由圖6 可知，系統受到階躍擾動后，Ut2和γ 出現了一定程度的振蕩，Pdc2出現了輕微波動，而隨著Pdc2減少，Ut2和γ 的振蕩幅度均減小。根據3.2.3 節分析可知，隨著Pdc2減少，在系統逆變側，LCC控制回路與MMC無功控制回路間的耦合程度基本不變，而MMC有功、無功控制回路間的耦合程度減弱，Ut2的控制效果提升，故Ut2的振蕩幅度有所減小；MMC有功、無功控制回路間的耦合程度減弱，Pdc2的控制效果受MMC 無功控制回路耦合作用的影響減弱，故Pdc2的波動略有減輕；LCC 控制回路與MMC 無功控制回路間的耦合程度基本不變，但受Ut2振蕩幅度減小的影響，γ 的振蕩幅度也有所減小。綜上，仿真結果與3.2.3節基于RGA的定量分析結果基本一致。

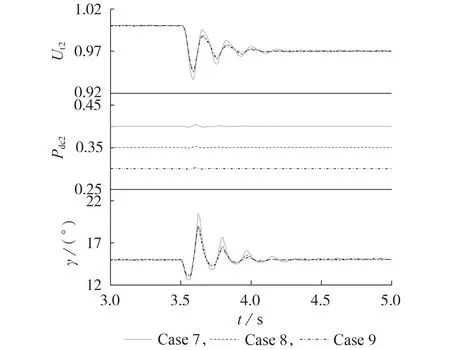
圖6 Case 7—9下的Ut2、Pdc2、γ波形Fig.6 Waveforms of Ut2，Pdc2 and γ in Case 7-9

4.4 直流系統功率振蕩頻率

直流功率調制作為直流附加控制系統的重要組成部分，已在實際直流工程中得到應用［18‐19］，該附加控制在抑制交流線路功率低頻振蕩時會引起直流傳輸功率的振蕩。

為驗證混合雙饋入直流輸電系統控制回路間的耦合程度受直流系統功率振蕩頻率的影響，當kSCR=1.5、L=50 km 時，設LCC-HVDC 整流側定直流電流參考值為1.8 kA，MMC-HVDC 逆變側定有功功率參考值為350 MW，3.5 s 時在350 MW 的基礎上附加不同頻率的擾動信號，仿真結果見圖7。Case 10—12這3 種工況下附加擾動功率分別為20 cos（πt）、20 cos（2πt）、20cos（4πt）。

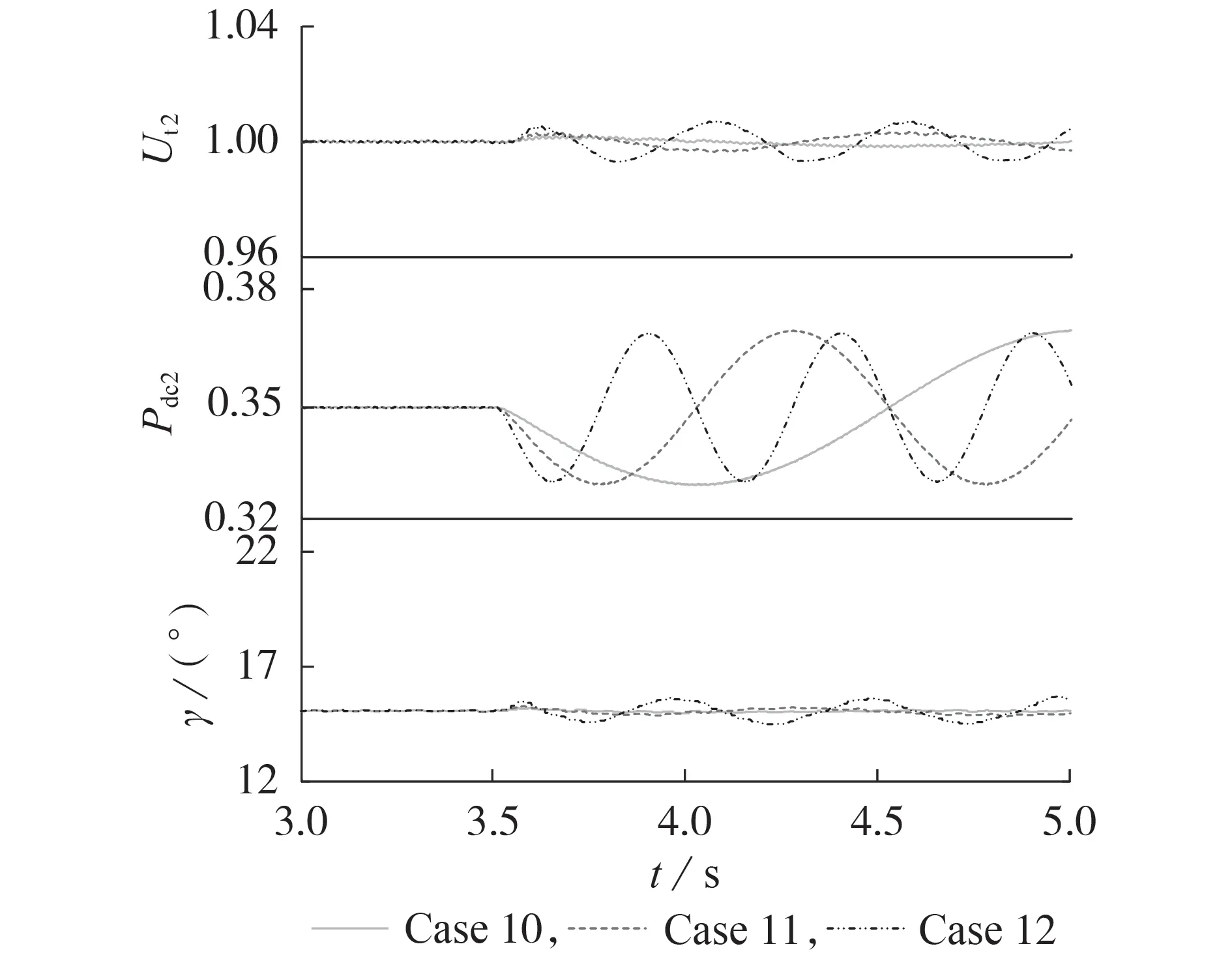
圖7 Case 10—12下的Ut2、Pdc2、γ波形Fig.7 Waveforms of Ut2，Pdc2 and γ in Case 10-12

由圖7 可知，隨著MMC 輸送功率振蕩頻率的提高，γ 和Ut2的振蕩幅度均逐漸增大；Pdc2振蕩導致Ut2的振蕩，Ut2的控制效果受其他控制回路間耦合作用的影響。根據3.2.4 節分析可知，在影響MMC 無功控制回路控制效果的因素中，LCC 控制回路與MMC無功控制回路間的耦合作用占主導地位，因此直流系統功率振蕩頻率提高時，LCC 控制回路與MMC 無功控制回路間的耦合程度加深，Ut2的控制效果變差，故Ut2的振蕩幅度增大；隨著直流系統功率振蕩頻率的提高，LCC 控制回路與MMC 無功控制回路間的耦合程度逐漸加強，γ 的控制效果受MMC 無功控制回路耦合作用的影響加深，故γ 的振蕩幅度增大。綜上，仿真結果與3.2.4節基于RGA的定量分析結果基本一致。

5 結論

本文利用控制理論中的RGA 方法定量分析了混合雙饋入直流輸電系統逆變側各控制回路間的耦合程度，分析了受端交流系統強度、聯絡線長度、直流功率傳輸水平以及直流系統功率振蕩頻率等多種因素對混合雙饋入直流輸電系統控制回路間耦合程度的影響，仿真結果驗證了理論分析的正確性，得到如下結論。

（1）揭示了存在于混合雙饋入直流輸電系統各控制回路間的耦合作用。在混合雙饋入直流輸電系統逆變側，當LCC 采取定關斷角控制、MMC 采用定有功定交流電壓控制時，LCC 與MMC 間的耦合作用主要存在于LCC 控制回路與MMC 無功控制回路之間，而MMC 有功、無功控制回路間的耦合作用僅在饋入極弱交流系統的情況下出現。

（2）通過對穩態RGA 的定量分析得到了混合雙饋入直流輸電系統中各控制回路間的耦合程度與受端交流系統強度、聯絡線長度以及直流功率傳輸水平的關系，在系統逆變側，LCC 控制回路與MMC 無功控制回路間的耦合程度分別隨受端交流系統強度的減小、聯絡線長度的減小、LCC 功率傳輸水平的提高而增強，而受MMC 功率傳輸水平的影響較小；MMC 有功、無功控制回路間的耦合程度分別隨受端交流系統強度的減小和直流系統功率傳輸水平的提高而增強，而受聯絡線長度的影響較小。

（3）通過對基于頻率RGA 的定量分析得到了混合雙饋入直流輸電系統中各控制回路間的耦合程度與直流系統功率振蕩頻率的關系，在系統逆變側，隨著振蕩頻率的提高，LCC 控制回路與MMC 無功控制回路間的耦合程度加強，MMC 有功、無功控制回路間的耦合程度先加強后減弱；在頻率變化過程中，LCC 控制回路與MMC 有功控制回路間的耦合作用始終較弱，LCC 控制回路與MMC 無功控制回路間的耦合作用始終強于MMC 有功無功控制回路間的耦合作用。

現有文獻對混合雙饋入直流輸電系統交互作用分析的角度主要集中于交流系統強度及系統穩定性等方面，而本文則聚焦于控制回路間的耦合程度對其控制性能的影響，因此本文的研究方法可以為定量分析混合雙饋入直流輸電系統內部的交互影響提供新思路。

附錄見本刊網絡版（http：//www.epae.cn）。