基于深度學習高中數學中問題設計策略研究

杜忠芬

摘要：深度學習離不開學生的自主思考，為了激發學生的思考能動性，教師需要關注學生的內心想法，著眼于學生的身心成長規律，精心設計不同的問題，通過問題來引導學生培養學生良好的思維習慣以及學習習慣。對于高中數學來說學生的深度學習非常關鍵，教師可以采取簡單設問的形式讓學生帶著問題自主剖析和大膽探索，這一點對打造品質課堂，促進學生的個性化發展有非常重要的作用和影響。

關鍵詞：深度學習;高中數學;問題設計;策略研究

引言

在新一輪課程改革的過程中高中數學教師所面臨的外部環境和形勢越來越嚴峻，為了突破時空限制，實現對癥下藥和與時俱進，高中數學教師需要反思教育行為，整合利用多種現代化的教育教學方式。通過設計具有一定吸引力的問題來促進學生的深度學習，高效學習和個性化學習，讓學生能夠自主分析、大膽想象，逐步提升學生的數學核心素養。

一、深度學習

深度學習十分注重知識學習的深入理解以及自主判斷，學生需要主動串聯不同的知識點，有機整合學習內容，構建完善的知識體系，提升個人的學習能力。不同知識點的有效梳理非常關鍵，這一點對學生知識網絡的構建有重要影響，教師需要關注學生的深度學習過程，將深度學習與構建反思相結合，采取循序漸進的形式促進的學生的知識遷移。知識運用以及問題解決最為關鍵，教師需要結合學生的學習狀態，學習結果，知識呈現方式和學習目標來調整教育教學進度，改革傳統的教育教學模式，在設置教學情境的過程中幫助學生高效解決問題，提升學生活學活用及舉一反三的能力。高中數學的邏輯性和實踐性比較明顯，教學難度、學習難度偏高，學生的深度學習不容忽略。教師需要以培養學生的學科核心素養為終極目標，積極利用深度學習這一重要的工具提升學生對學科本質知識的理解及認知，合理滲透不同的現代化教育元素，為學生的深度學習和自主反思做好前期鋪墊。

二、基于深度學習高中數學中問題設計必要性

學生的深度學習既考驗著學生的學習能力和思維邏輯水平，又考驗著教師的基本功。要想確保高中生在學習數學的過程中實現深度學習，教師需要以問題設計為出發點和落腳點，以系統性和連貫性的問題為基礎，做到層次分明和逐步攻克，讓學生能夠在分析問題的過程之中實現深入思考，自主探索，順利完成教師所布置的學習任務。問題教學法比較復雜，教師需要注重課堂教學秩序，實現環環相扣，按照一定的邏輯順序，在層層推進的過程中與學生共同分析問題并提出最佳的解決策略。如果教師能夠結合學生的深入度學習要求精心設置不同的問題，開展相應的教學實踐活動，提升數學課堂的吸引力，那么對體現以人為本的育人理念將會有重要的影響。學生也會在深度學習以及自主思考問題的過程中意識到數學學習了樂趣和奧秘，產生耳目一新的感覺，進而全程參與、自主學習。教師的教學壓力較輕，能夠更好的與學生進行交流及緊密溝通，在師生互動的過程中實現教學相長。

三、基于深度學習高中數學中問題設計策略

（一）靈活利用題目變式

新課改之后的高中數學教學變動顯著，教師需要結合學生的最近發展區，通過與學生之間的互動及交流，全面激發學生的探究欲望和學習能動性，主動設置問題鏈，在變式教學的過程中引導學生主動回答數學問題。概念本質特征的分析是第一步，教師需要主動變更問題條件以及結論，轉化問題內容及形式，精心創設不同的問題情境，整合利用多種教學方式按照同一個知識點設置一連串的問題，讓學生能夠鞏固個人已有的知識印象，實現深入理解和自主判斷。掌握問題的本質，了解問題的來龍去脈，分析問題背后的知識，這一點對學生的深度學習有重要作用和影響。

例如，在高一數學必修第一冊《函數的概念及其表示》一課時，在學習函數概念時，教師就可以靈活利用題目變式，展開三問。第一問：一張白紙，把它撕成兩份，之后重疊。重疊后再撕一次，再重疊再撕一次，撕扯3次后把所有的紙重疊放置有多少層？5次？15次呢？教師第二問，若一張紙厚0.1毫米，那么撕紙14次后把所有的紙重疊放置有多高？有一個人高嗎？若撕掉20次呢？教師第三問，建立“紙張y與撕紙次數x”之間的函數關系式？通過這樣一組由特殊到一般的題目變式，幫助學生建立感性經驗，激發學生數學思維。

（二）串聯不同的知識點

高中數學中的知識點比較繁瑣，具有明顯的層次性和邏輯性，邏輯聯系不容忽略。為了讓學生了解知識的本身和特質，教師需要在遷移知識和應用知識的過程中精心設計問題，鼓勵學生自主對比、綜合學習，深化學生對知識的理解，這種串聯知識點的教育教學模式對體現學生的主體價值有重要的影響。學生也能夠按照教師的要求，在簡單模仿的過程中實現大膽創新，主動按照自己的學習經驗自主串聯知識點，構建完善的邏輯思維框架，形成整體的認知結構和體系。

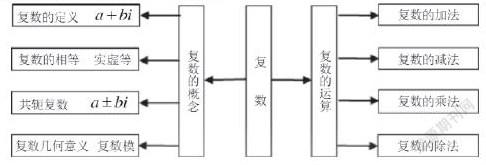
例如，在高一數學必修第二冊《復數》一單元，教師可以將這個單元下的每個小單元，復數的運算、復數的概念作為體系主體，再由每個小主體去延伸不同的知識點，由復數的運算延伸“復數的加法、復數的減法、復數的乘法、復數的除法”由復數的概念延伸“復數的定義 a+bi 復數的相等-實虛等，復數幾何意義-復數模，共軛復數-a±bi”將知識串聯構建復數整體認知結構，如圖：

通過這種方式，在很大程度上實現了學生主動構建，豐富了思維，提高了學生數學核心素養。

（三）引導學生理解概念

概念學習是基礎，是學生實踐應用的前提和必備條件。教師需要以學生的概念理解為依據，關注學生的數學概念學習情況，注重對學生錯誤概念的有效糾正，了解不完整概念以及偏差概念的負面影響。做好前期準備工作，關注學生的薄弱之處并設計針對性的問題，讓學生帶著問題進行分析以及思考，強化學生的概念理解能力以及邏輯思維能力。大部分學生能夠打下扎實基礎，留下深刻印象，自主自覺的調整學習進度，反思學習行為，產生耳目一新的感覺。

例如，在高一數學必修第二冊《平面向量》一課時，教師在將概念時可以運用問題引導，已知平面向量abc滿足a+b+c=0。且a與b的夾角為130°度。C與b的夾角為110°，ΙcΙ=4，那么ΙaΙ的值是多少？學生拿到這道題目后會先根據已知的條件畫出坐標，隨后教師引導學生思考，如a+b+c=0是條件的核心，嘗試把平面向量變成一個封閉三角形，用三角形的三角函數定理來解決問題。通過教師的引導，學生對平面向量有了一定的認識，認為平面向量即是一個幾何特征又有數學特征，通過這種方式讓學生意識到概念是理解不是死記硬背，而是將概念轉變成數學問題。

結語

要想促進學生的深度學習，高中數學教師需要調整教學思路，在精心設計問題的過程之中減輕學生的學習壓力及負擔，鼓勵學生自由發散，凸顯學生的主體價值，培養學生良好的學習習慣和自主探索的意識。學生的學習興趣高漲，學習能力和學習水平有了明顯的提升。

參考文獻：

[1]昝小紅.基于深度學習的高中數學單元設計教學策略研究——以"數列單元"為例[J].2021（2020-30）：43-44.

[2]張科.基于深度學習的高中數學新授課導學案編寫策略——以《余弦定理》導學案設計為例[J].福建中學數學，2020（10）：4.