尋找“面積變化”的秘密

□戎松魁

人教版《數學》教科書五年級上冊的第六單元是“多邊形的面積”。與該冊教科書配套的《教師教學用書》（以下簡稱《教學用書》）上提出了兩個與面積有關的問題，一個是圖形經過剪拼面積似乎變小了，另一個是圖形經過剪拼面積似乎變大了。按理說，圖形經過剪拼（不重疊）面積是不變的，而在這兩個問題中，面積似乎發生了變化，其“秘密”何在呢？就讓我們一起來尋找。

【問題1】如下圖，如果將圖1中的四塊幾何圖形裁剪開來重新拼接成圖2，我們將會發現，與圖1相比，圖2多出了一個洞！這怎么可能呢？理性會提出這樣的疑問。究竟是什么原因呢？老師們不妨先動動腦，想一想。（《教師用書》第231頁）

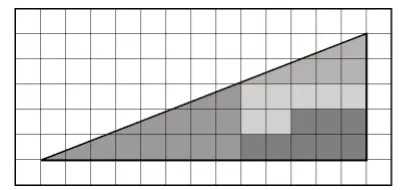
圖1

圖2

【尋找秘密】從圖1和圖2可以直觀地看到圖形經過剪拼出現了一個正方形的“空缺”，面積變小了，這怎么可能呢？秘密何在？

我們把圖1和圖2放到直角坐標系中來研究（如圖3、圖4所示）。

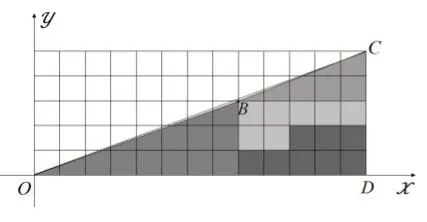
圖3

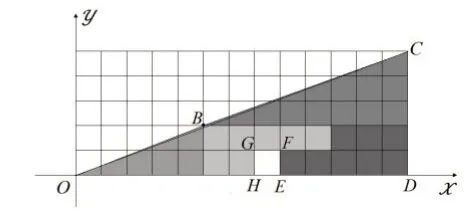
圖4

為了敘述方便，而且不失一般性，我們假設每個小正方形的邊長為1cm，并在多邊形的頂點上標上適當的字母。

由圖3可知，線段OB的斜率為，線段BC的斜率為，所以線段OB和BC不在同一直線上。連接OC，由于線段OC的斜率為，所以點B在線段OC的下方，四邊形OBCD的面積為S1=

由圖4可知，線段OB的斜率是，線段BC的斜率為，所以線段OB和線段BC也不在同一直線上。連接OC、OD，由于線段OC的斜率為，且，所以點B在線段OC上方。由此可知，經過剪拼得到的圖形（如圖4所示）其實是一個八邊形，這個八邊形OBCDEFGH的面積為與圖3中的四邊形OBCD面積相等。這就是說，剪拼前與剪拼后的圖形其面積是相等的。……