數學活動的特征、設計與組織原則*

顧大權

摘? ?要? ?數學活動是實施數學課堂教學的基本環節，是數學活動經驗獲得的主要途徑。分析數學活動的特征和內涵，會幫助教師科學地設計數學活動，合理地組織數學活動的教學，提高課堂教學效率，也會幫助學生積累數學基本活動經驗。

關鍵詞? ?數學教學? 數學活動? 教學設計

《義務教育數學課程標準（2011年版）》指出，數學活動是師生積極參與、交往互動、共同發展的過程。通過義務教育階段的數學學習，學生能獲得適應社會生活和進一步發展所必需的數學的基礎知識、基本技能、基本思想、基本活動經驗[1]。數學活動是獲得數學活動經驗的主要途徑，因此有必要去研究數學活動。數學活動的中心詞是“活動”，活動需要學生主體參與，活動能激發學生興趣，調動學生積極性，引發學生思考。數學活動的教學應從強調教學的結果性向強調教學的過程性轉變、從強調教師為主體教向強調學生為主體學轉變、從強調數學知識傳授向強調學生的素養發展轉變，這也是立德樹人教育任務和核心素養培育的要求，因此開展數學活動教學是當前課堂教學的需要。

關于數學活動的定義，各方還不統一，沒有一個明確的定義[2]。本文認為數學活動是由問題或操作入手、通過動手實踐操作或動腦思考、經歷數學化的過程、有數學思維參與的學習活動。分析數學活動的特征，理解數學活動的內涵，會幫助教師合理設計教學活動過程，順利開展數學活動的教學。

一、數學活動的特征

1.數學活動的抽象性

弗賴登塔爾認為：“數學活動是學生經歷數學化過程、建構數學知識的活動”。在數學活動中，學生要有足夠的時間經歷觀察、實驗、猜想、計算、推理、驗證等方式參與到活動中來，通過積極思考、交流形成自己的看法，發現其內涵，理解其含義。這一過程中學生必須經歷抽象、概括等數學化的過程，舍棄對象的其他屬性，僅研究數量關系、空間形式等數學屬性。學生在數學學習活動中，不斷對已有的結論進行抽象、概括建構形成新的知識，因此數學活動必須要經歷抽象、概括的數學化過程。

2.數學活動的思維性

斯托里亞爾認為：“數學教學是數學思維活動的教學”[3]。數學活動包括操作實踐等外部的行為活動和動腦思考、抽象概括等內部的思維活動。數學活動一般從教師組織材料、設計活動過程、組織動手實踐等外部的行為活動開始，到引發學生思考，開展合作交流、猜想驗證、反思質疑等方式的內部思維活動結束，其中要使現實中的問題或已有的結論在不斷抽象、概括等思維活動中形成新的結論或新的應用。操作實踐活動和數學思維活動相輔相成、相互影響，對知識的建構起著互相促進的作用。因此，數學活動離不開思維的參與，具有思維性。

3.數學活動的層次性

學生的數學學習過程是一個數學活動的過程，更是一個意義建構的過程[3]。教學過程中，從學生的已有知識經驗出發，到教學目標的實現，學生的認知圍繞“活動”來推動，當一個活動不能從學生的現有知識基礎順利到達最后的教學目標時，需要通過一系列的活動來過渡，這一系列活動之間要循序漸進，按照一定的層次來推進。前一個活動為后一個活動做鋪墊，后一個活動是前一個活動的深入，活動推動著學生達成教學目標。

4.數學活動的主體性

數學活動是師生積極參與、交往互動、共同發展的過程。有效的教學活動是學生學與教師教的統一，學生是學習的主體，教師是學習的組織者、引導者與合作者[1]。從建構主義的理論來看，學生的學習過程是知識建構的活動過程。由于學生知識基礎和活動經驗不同，活動中學生的參與度、對知識的理解、體驗也不一定相同，但必須堅持學生的主體地位，鼓勵學生猜想、辨析、思考、實踐和探索，用自己的方式解決問題，才能建構成為有效的知識，才能在活動中提升學生的素養和能力。

二、數學活動的設計

1.數學活動的內容設計

數學活動的內容包括操作實踐類活動和數學思維類活動，操作實踐類活動以操作步驟呈現，思維類活動以問題串的形式呈現。設計一個有效的數學活動需要有以下幾個條件：該活動能給學生創設良好的操作環境和問題情境，適合每一個學生參與;該活動能給學生營造一個探索空間，便于學生提煉與積累基本數學活動經驗;該活動能充分體現數學化的過程和數學思維的特點，讓學生通過活動看到數學活動內容的本質。因此，數學活動內容的設計要經歷數學化、要有數學思維參與，反應出數學活動內容的本質，這樣的數學活動才能獲得對數學活動的本質認識和深刻理解。

案例1：《數學》（蘇科版）九年級上冊“2.5直線與圓的位置關系（3）”的活動設計

問題1.要從一塊三角形鐵皮余料中剪一個圓，如何使剪得的圓面積最大？

問題2.圓的面積最大時，⊙O與三角形的三邊是什么位置關系？

問題3.要剪出這個圓，關鍵要找到什么？

問題4.由三條邊都是切線你想到了什么？

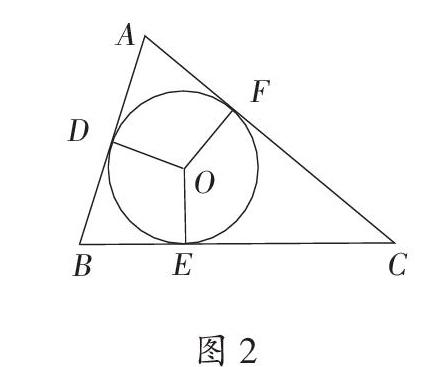
概念介紹：三角形的內切圓（見圖2）

問題5.能否給三角形的內切圓下個定義？

問題6.三角形的內切圓和圓外切三角形的“內”和“外”兩個字如何理解？“切”字又如何理解？

問題7.一個三角形有幾個內切圓？為什么？

【設計說明】問題1要讓學生經歷數學化的過程，將實際問題抽象成在一個三角形中畫一個圓，并且使圓的面積最大。問題2讓學生經歷操作探索、交流互動等主體活動，發現圓的面積最大時，就是圓和三角形的三邊都相切的時候，本質就是作一個圓，使它與三角形的三邊都相切。問題3、4就是要找圓心和半徑，圓心到三邊的距離相等，所以圓心就在三個角的平分線上，畫出兩個角的平分線，就確定出圓心，半徑就是圓心到三邊的垂線段，過圓心做一邊的垂線段，就確定了半徑。問題5、6、7通過對定義的文字認識加強對概念的理解。這個數學活動學生經歷去情境化，將實際問題變成數學問題，并提煉出共同的本質屬性，積累了數學化的活動經驗。在活動中經歷數學思維發現內心是怎樣形成的，知道了知識產生的來龍去脈，在操作的活動過程中獲得了隱性的數學知識，積累了數學活動的經驗。

2.數學活動的過程設計

知識產生的過程就是不斷面對新問題、發現新問題、提出新問題，解決新問題的過程。學生的認知方式也是通過經歷的活動實現再發現和再創造的過程，即從已有的數學知識經驗出發，對已有的知識經驗重新認識、重新發現、重新加工，這個過程需要通過活動來推動。從學生已有的知識經驗到教學目標的實現，可能需要多個活動才能達到，這時數學活動的設計要以一定的層次展開，各個活動之間層次清楚、脈絡分明、循序漸進，這樣才能將學生的認識帶到一個更高的層次上，使數學活動的本質得到落實。

案例2：《數學》（蘇科版）八年級上冊“6.1函數”的活動設計

活動1：隨著一天時間的變化，氣溫也隨之變化;隨著學生年齡的增長，體重越來越重;隨著國歌播放時間的進行，國旗的越升越高;隨著圓的半徑的增大，圓的面積越來越大……

活動2：

問題1.列車從甲地駛往乙地，在16：17到16：22這個時段，列車在勻速行駛的過程中有哪些量？在這些量中有哪些量是沒有變化的？哪些量是不斷變化的？

問題2.銀行對各種不同的存款方式都規定了相應的利率，下表是銀行公布的年利率：

存期x與年利率y有什么關系？

問題3如圖3，搭一個正多邊形圖案需要8根火柴棒，每多搭一個正多邊形圖案就要增加7根火柴棒，請說出搭正多邊形圖案過程中的常量和變量。

你能寫出搭n個正多邊形圖案所需的火柴棒數s與正多邊形個數n之間的關系式嗎？

活動3：請學生再列舉出一些生活中滿足上述屬性的實例，通過大量的實例，讓學生多角度、多層面認識和理解實例的本質屬性，并指出滿足上述本質屬性的例子就是函數，提煉這些實例具有的本質屬性，概括歸納并試著給函數下個定義。共同歸納表述函數的定義：一般地，在一個變化的過程中有兩個變量x和y，如果對于x的每一個值，y都有唯一的值與它對應，那么我們稱y是x的函數，x是自變量。

【設計說明】活動1從生活實際入手，從現實背景引領學生進行數學化，感受在變化過程中有兩個變量，一個量發生變化時，另一個量也在發生變化。活動2在活動1的基礎上逐漸深入，圍繞幾個問題的共同特征的本質屬性進行提煉：具有兩個變量，兩個變量之間存在著唯一對應關系，每當一個變量取一個定值，另一個變量有唯一的值與其對應。活動3在前兩個活動的基礎上繼續深入，通過大量的具體實例發現了函數的本質屬性，通過概括總結，讓學生對本質屬性有了完整的認識，在活動中逐層深入提煉出函數的本質屬性，并將函數的本質屬性進行符號化，利用數學符號來表征函數的概念。

三、數學活動的組織原則

1.確立學生在數學活動中的主體地位

有效的數學活動是學生學和教師教的統一，學生是學習的主體。教師要放手讓學生充分參與數學活動，讓學生有足夠的時間進行活動，并在活動中大膽去想、去做。學生在數學活動中的發現，教師要給學生平等交流和表達的機會，鼓勵學生去猜想，引導學生去驗證，找到合理的解決方法，才能在活動中建構數學知識。另外由于學生的知識基礎、活動經驗等存在的個體差異，活動中學生對知識的理解和體驗也有差異，因此活動中學生的交往互動、合作學習就很有必要，這樣才能真正實現從教師教到學生學的轉變，從知識傳授到素養提升的轉變。

2.發揮教師在數學活動中的引導作用

數學活動中應體現學生的主體作用，但由于學生自身經驗、基礎等局限，使得學生在數學活動中的體驗是淺層次的、模糊的，需要教師的幫助和引導，激活已有的經驗，形成更多的活動聯系點，提高活動的有效性。教師的有效引導可在活動處于無助的狀態下讓活動的目標更明確，不斷將活動引向更深的層次，讓學生的思維更加開闊，思路更加清晰，形成思想方法。教師的有效引導可以掌控數學活動的方向和進程，帶領學生經歷一個又一個活動層次，不斷解決問題又發現新問題，直至目標的實現，既符合學生的知識建構順序，又實現了不僅關注活動的結果，更加關注活動的過程的目的。

3.營造活動中寬松、和諧的文化氛圍

要確定班級活動中學生的主體地位，既要學生個人的獨立思考，又要學生之間的合作交流。中學生課堂上喜歡表現自己，但又比較敏感，常會擔心回答錯誤或操作失誤而受到老師的責備和同學的嘲笑。因此，營造寬松、和諧的班級文化氛圍會避免學生被批評和嘲笑，避免學生不愿意參加活動，不愿意和同學交流自己的真實想法，不愿意發表自己的見解，以沉默的方式對待，錯過了展示的機會，喪失了對知識的真正理解。教師應平等的對待每一位學生，給學生表達的機會，讓學生說出內心的想法，不因為學生的想法和教師不一致就強硬地扭轉學生的真實想法，不諷刺挖苦。同學之間要規范言行，傾聽別人的見解，發表自己的獨到見解，吸納與眾不同的觀點，營造互相信任和尊重的氛圍，讓學生無拘束的展示、交流和爭辯，才能發揮活動的作用。

參考文獻

[1] 馬復，凌曉牧.新版課程標準解析與教學指導[M].北京：北京師范大學出版社，2012.

[2] 潘小梅.初中數學教學研究入門36問[M].浙江：浙江大學出版社，2017.

[3] 王寬明，夏小剛.建構數學活動的要義及特征分析[J].教學與管理，2012（03）.

【責任編輯? 郭振玲】