對一道導數模擬題的研究

浙江省寧波效實中學(315012) 童益民

一、原題呈現

已知函數f(x)=lnx+mx(m為常數).

(1) 討論f(x) 的單調區間; (2) 當m≥時，設的兩個極值點x1,x2(x1＜x2)恰好為h(x)=2 lnx-ax-x2的零點，求的最小值.

該題是文[1]引自江西省上饒市2017年一模試題，通過對這題的研究，發現這是一道錯題，由于題目中出現的條件較多，起到一定的干擾作用，所以很難發現問題，現對該題的第(2)小題進行分析研究.文[1]中對第(2)小題的解答過程如下:

由g(x)=lnx+mx+得g′(x)=+m+x=由已知x2+mx+1=0 有兩個互異實根x1,x2，由根與系數的關系得x1+x2=-m,x1x2=1，因為x1,x2(x1＜x2)是h(x)的兩個零點，故

由 2○-①得:解得a=-(x2+x1)，因為h′(x)=-2x-a，得將a=(x2+x1)代入得

構造F(t)=lnt-得＞0，則F(t)=在[2,+∞) 上是增函數，所以F(t)mⅰn=F(2)=即y=(x1-的最小值為

二、錯題分析

錯誤1 分析因為的兩個極值點x2＞x1＞0，且所以x1+x2=-m ＞0，即m ＜0.又Δ=m2-4＞0，即m ＞2 或m ＜-2，所以m ＜-2，這樣原題中的m≥可改為這樣原解答過程和結果沒有影響.

把m的范圍改正后，其實還可以換一種更簡潔的方法，如下:

錯誤2 分析以上兩種方法采用不同的主元進行消參，第一種方法利用主元，第二種方法利用主元m，但得到的結果是兩種截然不同的答案，那么問題出在哪里?從已知條件可得到4 個等式從解方程組的角度，這四個變量x1,x2,m,a是確定的，所以的值是確定的，不應該求最小值.

三、深入探究

已知函數h(x)=2 lnx-ax-x2有兩個零點x1,x2，求證x1x2＞1.

證明:令h(x)=2 lnx-ax-x2=0，所以a=令所以令函數G(x) 的極值點為x0，可得2-2 lnx0=0，由此式可得x0＞1.所以函數G(x) 在(0,x0)上遞增，在(x0,+∞)上遞減，且0＜x1＜x0＜x2.

先證x1x2，即證因為且G(x) 在(x0,+∞) 上遞減，即證因為G(x1)=G(x2)，即 證G(x1)＜令H(x)=

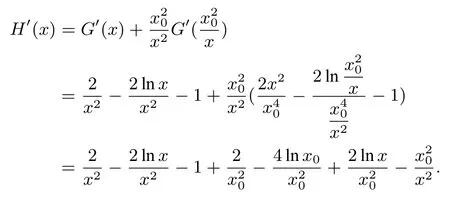
因為2 lnx0=2，所以

因 為2=-2 lnx0，所 以H′(x)=(x2-因為0＜x ＜x0，所以H′(x)＞0，所以函數H(x)在(0,x0)上單調遞增，所以當x ∈(0,x0)時，即即這樣先證明了又因為x0＞1，所以x1x2＞1.

改編題: 已知函數f(x)=lnx+mx(m ∈R).

(Ⅰ)討論f(x)的單調區間……