橢圓(雙曲線)焦點三角形中的一個不等式

廣州市禺山高級中學(511483) 藍賢光

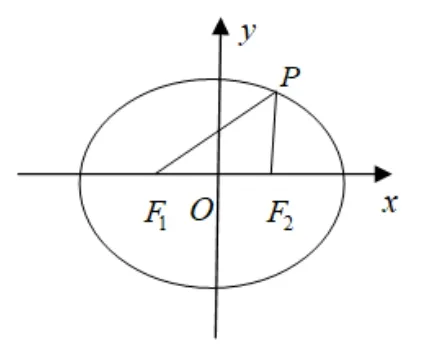
在高三的一次綜合訓練中有這樣一道填空題:

題目1設P是橢圓+y2=1 上異于長軸端點的任意一點，F1，F2是該橢圓的兩個焦點，∠F1PF2=60?，R，r是ΔPF1F2的外接圓和內切圓半徑，則=____.

解析顯然a=2，b=1，c=在ΔPF1F2中由正弦定理得

即R=2;又

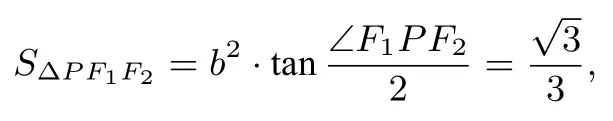
且

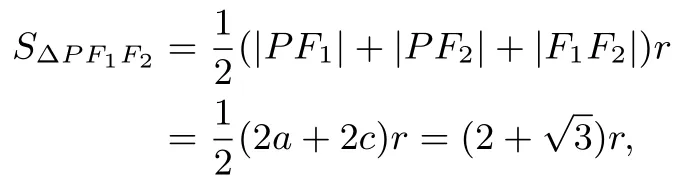
經探究，我們有以下的

性質1設P是橢圓=1(a ＞b ＞0)上異于長軸端點的任意一點，F1，F2是該橢圓的兩個焦點，e是該橢圓的離心率，∠F1PF2=2θ，R，r是ΔPF1F2的外接圓和內切圓半徑，則

證明在 ΔPF1F2中由正弦定理得 2R=即又b2·tanθ，且

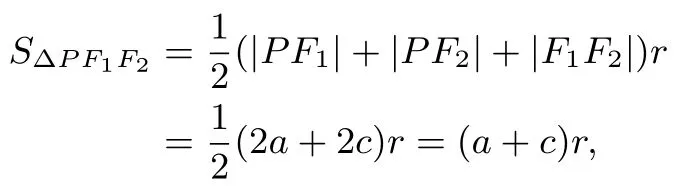
所以(a+c)r=b2tanθ，r==(a-c)tanθ，從而

設B是該橢 圓短軸的 一 個端點，∠OBF1=α，則0＜θ≤α ＜，sⅰnθ≤sⅰnα=，于是

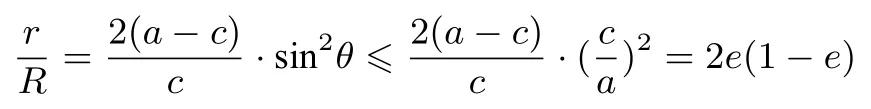
當且僅當sⅰnθ=sⅰnα=，即點P與點B重合時“=”成立，證畢!

將上述性質類比到雙曲線上去，我們又有以下的

性質2設P是雙曲線=1(a ＞0,b ＞0)上異于實軸端點的任意一點，F1，F2是 該雙曲線的兩個焦點，e是該雙曲線的離心率，∠F1PF2=2θ，R，r是ΔPF1F2的外接圓和內切圓半徑，則

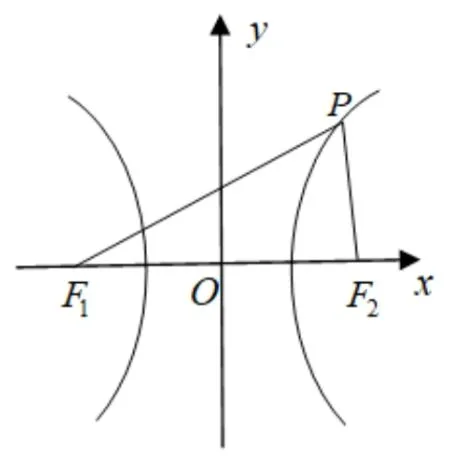
證明在 ΔPF1F2中由正弦定理得 2R=且

在ΔPF1F2中由余弦定理得:

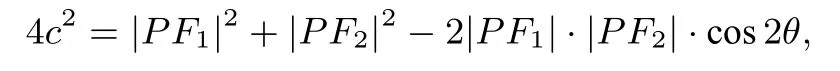
所以4c2=(|PF1|-|PF2|)2+2|PF1|·|PF2|·(1-cos 2θ)

或4c2=(|PF1|+|PF2|)2-2|PF1|·|PF2|·(1+cos 2θ),

于是，

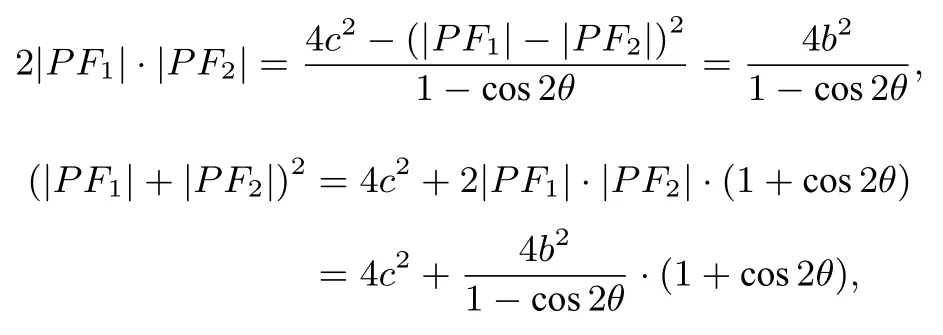
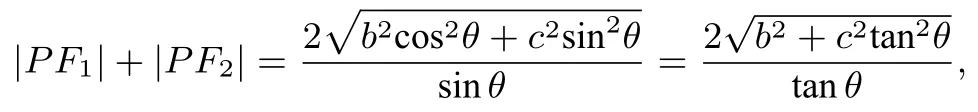
所以

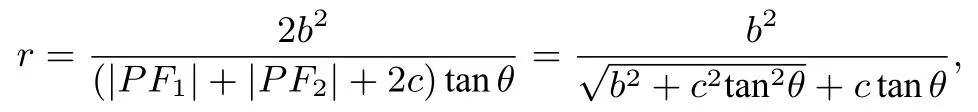
從而

當且僅當tanθ=時等號成立，此時可求得點P的坐標為